PHPに基づいたヒープソート原理の実装

ヒープ

ヒープは、コンピュータ サイエンスにおける特別なタイプのデータ構造の一般名であり、通常は配列です。ツリーとして表示できるオブジェクト。

ヒープ{k1,k2,ki,…,kn} (ki = k2i,ki >= k2i 1), (i = 1,2,3,4...n/2)

ヒープについて:

• ヒープ内のノードの値は常に親ノードの値以下、またはそれ以下ではない;
• ヒープは常に完全なバイナリ ツリーです (下記)。
• 最大のルート ノードを持つヒープは最大ヒープまたは大ルート ヒープと呼ばれ、最小のルート ノードを持つヒープは最小ヒープまたは小ルート ヒープと呼ばれます。

完全なバイナリ ツリー

ヒープのソートに関して言えば、完全なバイナリ ツリーについて言及する必要があります。これらの基本概念はインターネット上のあらゆる場所にあります。最も単純なものを選択しました。 。

完全な二分木: 最後の層を除いて、各層のノード数は最大に達し、最後の層では右側のいくつかのノードだけが欠落しています。

私自身の結論は、それはまさに次の 2 つの特徴によるものであるということです。

• 最後の層のみが空のノードを持つことが許可され、空のノードは右側にあります。 、リーフ ノードは次の 2 つの最大レベルにのみ表示されます (保存方法の規則性);
• i>1 の場合、ツリーの親はtree[i p 2] (親ノードと子ノードの値の規則性) );

を使用すると、並べ替えが非常に便利になります。

ヒープ ソート

ヒープ ソートでは、昇順には大きな上部ヒープが使用され、降順には小さな上部ヒープが使用されます。

この例では、上部の小さなヒープを降順で使用して分析します。

ヒープのソート手順は次のとおりです:

1. データ (49、38、65、97、76、13、27) から配列 $arr を作成します。 , 50) ;

2. 配列 $arr を使用して、スモール トップ ヒープを作成します (主な手順はコード コメントで説明されています。以下の図は、配列を使用してスモール トップ ヒープを作成するプロセスです) heap);

3 、ヒープのルート (最小要素) を最後のリーフと交換し、ヒープの長さを 1 つ減らして、2 番目のステップにジャンプします;

4ヒープ内にノードが 1 つだけになるまで手順 2 ～ 3 を繰り返し、ソートが完了します。

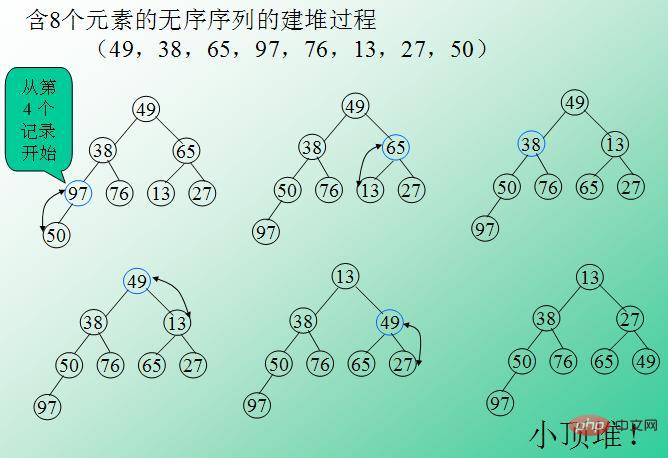
# ヒープ ソートの PHP 実装

##

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2; 
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);

//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);

for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);  
}

//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
  //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
  //从$index处对一个树进行循环比较,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左节点,将其下标存进最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }  
    }
  }
}

//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

以下はソートの最終結果です。 :

完全なソートにはヒープが使用され、時間計算量は O(nlogn)

完全なソートにはクイック ソートが使用され、平均時間計算量はも O( nlogn)

しかし、ヒープ ソートを使用して TopK を見つけることができる場合、K ラウンドのソートのみが必要なため、ヒープの時間計算量は O(Klog2(n) になります。

推奨チュートリアル：《

PHP

》

以上がPHPに基づいたヒープソート原理の実装の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。