ホームページ >バックエンド開発 >PHPチュートリアル >プログラマーさん、あと何年これができるでしょうか?
プログラマーさん、あと何年これができるでしょうか?
- 雷果国オリジナル
- 2020-06-19 10:55:10276ブラウズ
テクノロジーの波は際限なく押し寄せる 波が去った後、私たちに残されるのは方法論でしょうか?それとも時代遅れのテクノロジーでしょうか?
------
私たちプログラマーは、まるで「35歳の呪い」がプログラマーの専売特許になったかのように、いわゆる「35歳の呪い」について話すのが好きです。しかし、実際には、35歳という年齢はあらゆる分野のプロフェッショナルにとって直面する問題です。
基本的に、35歳は中年に達する分岐点であり、仕事での価値生産が体力に依存するようになると、キャリア形成が低下し始めるというジレンマに直面することになるでしょう。
プログラミングは本来、抽象的な思考と論理的推論を重視する非常に創造的な仕事ですが、私たちの中には、プログラミングを水のように平凡な仕事のように扱っている人も少なくありません。呪い」という意志が私たちを悩ませます。
社会的集団では、さまざまな人がさまざまな選択肢を持っています。私には環境全体を変えるつもりはありませんし、変えることはできませんが、「35 歳の呪い」と戦う意欲のあるプログラマーが何らかの方向性を見つけて取り組むのを手助けできればと思っています。あと数年!
面接の質問から始めましょう
ヤン・フイの三角形は、私が面接でよく尋ねる質問です。「指定された形式に従って、ヤン・フイの三角形の最初のN行をプログラムして出力してください。」
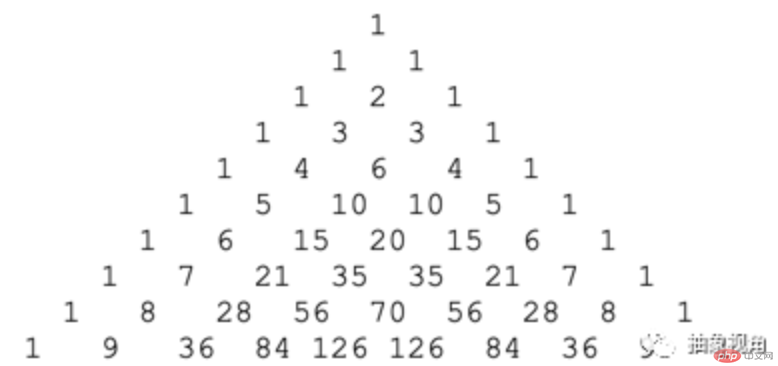
ほとんどの受験者は、質問を受けた後、コーディングを開始し、最初に 2 層のループを作成し、その後、ループの終了条件について考え始めました。しかし、彼らは、自分でも信じられない答えを出しました。 。最も印象的だったのは、WeChat Pay の候補者がデータの最初の N 行を取得する方法だけを提供したが、指定された形式で印刷する方法がまだ見つからなかったときです。
多くの人は、数年間学校を辞めた後、アルゴリズムを忘れたと言うでしょう。この種の質問は、学校が採用した生徒に尋ねるべきです。私が気にしているのは特定のアルゴリズムではなく、問題を分析して解決するという考え方です。私たちはいくつかの特定のアルゴリズムを忘れることができますが、忘れている間に、アルゴリズムに含まれる問題解決のアイデアを自分の武器として内面化する必要があります。
次に、この問題について私がどのように捉えているかを紹介します。
チューリング賞受賞者の N. ヴィルスは「プログラム = アルゴリズム + データ構造」を提案しましたが、私は「プログラム = データ + プロセス」と言うほうが馴染みがあります。
データの観点
まず第一に、このインタビューの質問をデータの観点から見てみると、次のことがわかります。
1. 2 次元配列 (PHP 言語を例にとります) を使用して、 Yang Hui の三角形の最初の N 行のデータ
[ [1], [1, 1], [1, 2, 1], [1, 3, 3, 1], ]
2。データの行間には次のルールが存在します:
1) 各行の両側の数字は常に 1 です
2) 各行の中央の数字は、前の行の交点にある 2 つの数値の合計です
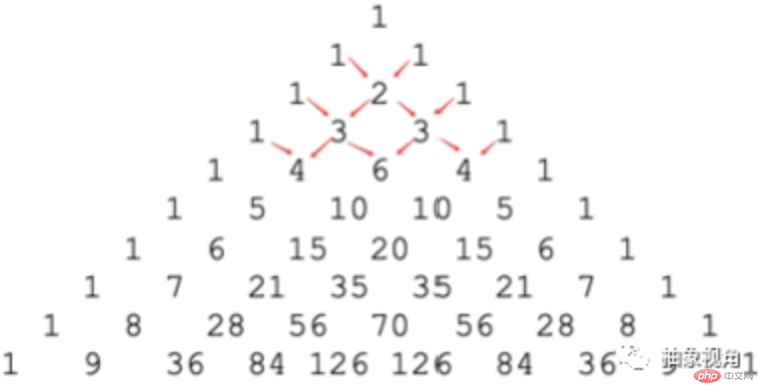
したがって、この関係は疑似コードで説明できます:
F(1) = [1]
F(N) = [
1,
F(N-1)[0] + F(N-1)[1],
F(N-1)[1] + F(N-1)[2],
...,
F(N-1)[N-2] + F(N-1)[N - 1],
1
]プロセスの観点
次に、このインタビューの質問をプロセスの観点から見ていきます。まず、そのプロセスは 2 つのステップに分けることができます: 1) Yang Hui 三角形の最初の N 行のデータを取得します。 2) 図に示されている位置合わせに従って印刷します。
最初のステップでは、以前のデータ分析に基づいて、対応するメソッド設計を簡単に描画できます:
function yanghui_datas($n); // 获取前N行杨辉三角数据 function yanghui_line_datas($prev_line_data); // 依据前一行数据获取下一行数据
2 番目のステップでは、図の位置合わせに従って印刷します。純印刷は非常にシンプルなので「位置合わせ」がポイントです。
位置合わせの問題を解決する方法は、対応する位置を空白のままにすることです。しかし、空白をどのように残すかが明確ではないことがわかりました。さらに考えてみましょう。空白の領域で論理が不明瞭になる原因となる難しい問題は何でしょうか。
分析すると、最初の 5 行だけを出力する必要がある場合、各数値は 1 桁になり、6 行目を出力する場合は、10 桁から始まることがわかります。したがって、ここで困難を生み出すのは、数値の幅に関する不確実性です。
逆に考えると、数字の幅が決まっていれば、そんな難しいことはありません。したがって:
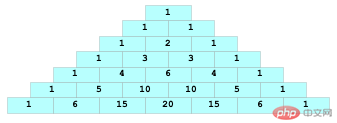
各数値を等幅のグリッドに配置します。このようにして、問題全体が明らかになります。
格子宽度 = 最大数字宽度 + 1 行前留白 = (LINE_COUNT - LINE_NO) * 格子宽度 / 2 格子内部: (数字居中) 左留白 = (格子宽度 - 数字宽度) / 2 右留白 = 格子宽度 - 左留白 - 数字宽度
上記の分析後、コードはほぼ紙に表示されます。
// 获取前N行杨辉三角数据
function yanghui_datas($n_line) {
$datas = [];
$prev_line_datas = [];
while ($n_line -- > 0) {
$line_datas = yanghui_line_datas($prev_line_datas);
array_push($datas, $line_datas);
$prev_line_datas = $line_datas;
}
return $datas;
}
// 通过前一行数据获取下一行数据
function yanghui_line_datas($prev_line_datas) {
if (empty($prev_line_datas)) {
return [1];
}
$line_datas = [];
array_push($line_datas, 1); // 行首
for ($i = 1; $i < count($prev_line_datas); $i ++) {
array_push($line_datas, $prev_line_datas[$i - 1] + $prev_line_datas[$i]);
}
array_push($line_datas, 1); // 行尾
return $line_datas;
}
// 打印指定的杨辉三角数据
function yanghui_print($datas) {
$space = ' '; // 留白字符
$newline = '<br />'; // 换行符
$max_num = yanghui_max_num($datas); // 最大数字
$max_num_width = yanghui_num_width($max_num); // 最大宽度
$unit_width = $max_num_width + 1; // 格子宽度
$line_count = count($datas); // 行数
foreach ($datas as $idx => $line_datas) {
$line_no = $idx + 1; // 行号
$line_prefix_width = ($line_count - $line_no) * $unit_width / 2; // 行前留白数
echo str_repeat($space, $line_prefix_width);
foreach ($line_datas as $num) {
$num_width = yanghui_num_width($num); // 数字宽度
$left_width = intval(($unit_width - $num_width) / 2); // 格子内左留白宽度
$right_width = $unit_width - $left_width - $num_width; // 格子内右留白宽度
echo str_repeat($space, $left_width);
echo $num;
echo str_repeat($space, $right_width);
}
echo $newline;
}
}
// 获取最大数
function yanghui_max_num($datas) {
$max = 0;
foreach ($datas as $line_datas) {
foreach ($line_datas as $num) {
$max = max($max, $num);
}
}
return $max;
}
// 获取数字的宽度
function yanghui_num_width($num) {
return strlen(strval($num));
}最終的に、プロセスの 2 つの部分が組み立てられて、望ましい結果が得られます。
function yanghui_dump($n) {
$datas = yanghui_datas($n);
yanghui_print($datas);
}追加
ヤン・ホイの三角形の数値は座標に基づいて直接計算できると言う人もいますが、それは問題ではなく、データの対応する部分を置き換えるだけです。
啓発
私たちが問題に直面したとき、経験ベースと能力ベースの 2 つの思考モードがあります。
経験的に考え、自分の知識ベースを検索したところ、Yang Hui の三角形は 2 層のサイクルであることがわかり、それを実行し始めました。1 つのステップを実行した後、次の質問が自分の中にないことがわかりました。知識ベースを読んでから、瞑想に夢中になりました。
能力思考、最初に問題の本質的な構成要素を分析し、問題を分解し、複雑な大きな問題を複数の単純な小さな問題に変換し、繭を剥がし、それぞれの小さな問題に対する答えを自分の知識ベースで検索し、最後に質問を解決します。
2 つの思考モードの長所と短所は明らかです。経験ベースの思考は、特定の既知の単純な問題を解決するのに適しており、能力ベースの思考は、不確実で未知の複雑な問題を解決するのに適しています。幅広い適応性を備えています。
プログラミングを通じて有能な思考を鍛えます
プログラミングは、論理と推論に焦点を当てた非常に創造的な仕事です。
プログラミングを始める前に、まず対象システムを具体的な問題の観点から分析する必要があります。次に、より高いレベルの演繹を行うために、抽象的な観点から対象システムを分析する必要があります。具体と抽象の間で、私たちは現実の合理的な抽象的な説明を見つけるために常に熟考します。
この分析と推論のプロセスは、物事の本質を見つけるプロセスです。しかし、私たちは日々の業務において多くの複雑な要求に直面しており、設計レベルを考える時間はあまりありません。現実は私たちを需要翻訳機械に変えました。
ほとんどのプログラマーは実際にはこれをやりたがらないので、変更を求める学生を支援し、そのような変更の達成を促進するためにチュートリアルを使用したいと考えています。
2014 年に、現在会社で使用されているフレームワークを作成しました。これは 5 年以上安定して実行されており、600,000 行を超えるビジネス コードをサポートしていますが、コードは 6,000 行しかありません。次回はこれをブループリントとして、フレームワークを書き直すという観点から、フレームワークを書く際の思考・分析・設計・実装の全プロセスを網羅的に再現し、ビデオチュートリアルとしてまとめたいと思います。誰もがプログラミングの感覚を見つけるのに役立つことを目指しています。 (自発的な支払い、共有と拡散は無料)
チュートリアル全体は大まかに 12 の講義に分かれており、各講義には独立したテーマがあり、各講義は 1 ~ 3 時間続き、公開アカウントの記事が付いています。大規模なフレームワークは、外部環境との対話、ビジネス層のカプセル化制約、ORM などの補助ツールの 3 つの部分に分かれています。
チュートリアル
テキストの表現力が限られているため、この記事はキャリア開発の具体的な分析、チュートリアルで伝えたい価値、価値を伝えるために使用される方法については、導入としてのみ使用されますので、ダウンロードしてください。詳細な学習のためのビデオチュートリアル。
[Ten Years of Sword, Understanding Abstract Thinking through Frameworks] は、私が記録した一連のチュートリアルであり、フレームワーク開発の思考、分析、設計、実装のプロセス全体を再現することで、誰もがプログラミングのインスピレーションを見つけるのに役立ちます。支払い、無料の配布と共有)。チュートリアルは公開アカウント「Abstract Thinking」を通じて公開されます。
今日公開されるのは、最初の講義「チュートリアルを録画する意味」です。興味があり、さらに詳しく知りたい場合は、QR コードをスキャンしてビデオチュートリアルをダウンロードしてください (アドレス: https://pan.baidu. com/wap/init?surl =IZ24Az5GFpQoQSD4WbfR8g 抽出パスワード: rcga)
以上がプログラマーさん、あと何年これができるでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

