Python 再帰関数、二分探索アルゴリズムの概要

1. 初期再帰

再帰関数: 関数内で関数自体を呼び出します。

再帰の最大深さ: 998

先ほど見たように、再帰関数は外部の力によってブロックされない限り実行を続けます。しかし、関数呼び出しの問題については以前に説明しました。関数呼び出しごとに独自の名前空間が生成されます。連続して呼び出されると名前空間がメモリを占有しすぎるため、Python はこれを防止しようとしています。再帰レベルの数を強制的に 997 に制御します (997 まで! 損をすることも、だまされることもありません...)。

この「998 理論」を証明するために使用できるもの「？ここで実験を行うことができます:

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

このことから、エラーが報告されるまでに確認できる最大数は 998 であることがわかります。もちろん、997 はメモリ最適化のために Python によって設定された数値です。私たちのプログラム. デフォルト値, もちろん、何らかの方法で変更することもできます:

import sys
print(sys.setrecursionlimit(100000))

この方法で再帰の最大深さを変更できます. Python で許可される再帰の深さを 10w に設定するだけです。実際の再帰の深さは、到達可能です。深さはコンピュータのパフォーマンスに依存します。ただし、このデフォルトの再帰の深さを変更することはお勧めしません。997 レベルの再帰で問題を解決できない場合は、問題を解決するために再帰を使用するのが適切でないか、コードの書き方が不十分であるかのどちらかです~~~

この時点で、再帰はそれほど良いものではなく、while True ほど便利ではないと感じるかもしれません。しかし、世の中には「人間は循環を理解し、神は再帰を理解する」という格言があります。再帰関数を過小評価しないでください。再帰の本当の意味を理解できなかったため、多くの人が長年にわたって偉大な巨匠の境地に足を踏み入れることができませんでした。そして、私たちが将来学習するアルゴリズムの多くは再帰に関連するものになります。さあ、それを学んだ場合にのみ、それを嫌いになる資本が得られます。

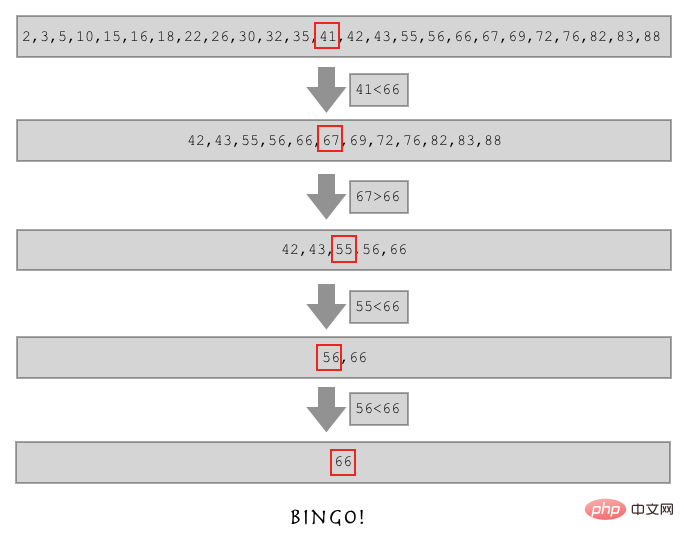
2. 再帰の例の説明

ここでは、再帰で何ができるかを説明するために別の例を示します。

例 1:

ここで、アレックスさんは何歳ですかと尋ねます。言わないって言ったけど、アレックスはエゴンより2歳年上だよ。

アレックスの年齢を知りたければ、やはりエゴンに聞く必要がありますか?エゴンは、「私も言わないけど、私はウー卿より2歳年上です」と言いました。

あなたは再び呉卿に尋ねましたが、呉卿も教えてくれませんでした。彼は自分が太白より 2 歳年上だと言いました。

次に、タイバイに尋ねると、タイバイは自分は 18 歳だと答えます。

この時点でご存知でしたか？アレックスは何歳ですか?

##2武様203エゴン224アレックス24

　　你为什么能知道的？

　　首先，你是不是问alex的年龄，结果又找到egon、武sir、太白，你挨个儿问过去，一直到拿到一个确切的答案，然后顺着这条线再找回来，才得到最终alex的年龄。这个过程已经非常接近递归的思想。我们就来具体的我分析一下，这几个人之间的规律。

age(4) = age(3) + 2 
age(3) = age(2) + 2
age(2) = age(1) + 2
age(1) = 40

　　那这样的情况，我们的函数怎么写呢？

def age(n):
    if n == 1:    
      return 40
    else:     
         return age(n-1)+2print(age(4))

　　如果有这样一个列表，让你从这个列表中找到66的位置，你要怎么做？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

　　你说，so easy！

　　l.index(66)...

　　我们之所以用index方法可以找到，是因为python帮我们实现了查找方法。如果，index方法不给你用了。。。你还能找到这个66么？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
i = 0for num in l:    if num == 66:
        print(i)
    i+=1

　　上面这个方法就实现了从一个列表中找到66所在的位置了。

　　但我们现在是怎么找到这个数的呀？是不是循环这个列表，一个一个的找的呀？假如我们这个列表特别长，里面好好几十万个数，那我们找一个数如果运气不好的话是不是要对比十几万次？这样效率太低了，我们得想一个新办法。

二分查找算法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

　　你观察这个列表，这是不是一个从小到大排序的有序列表呀？

　　如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？

　　这就是二分查找算法！

　　那么落实到代码上我们应该怎么实现呢？

　　简单版二分法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]def func(l,aim):
    mid = (len(l)-1)//2
    if l:        if aim > l[mid]:
            func(l[mid+1:],aim)        elif aim < l[mid]:
            func(l[:mid],aim)        elif aim == l[mid]:
            print("bingo",mid)    else:
        print(&#39;找不到&#39;)
func(l,66)
func(l,6)

　　升级版二分法

l1 = [1, 2, 4, 5, 7, 9]
def two_search(l,aim,start=0,end=None):
    end = len(l)-1 if end is None else end
    mid_index = (end - start) // 2 + start    
    if end >= start:
            if aim > l[mid_index]:
                        return two_search(l,aim,start=mid_index+1,end=end
             elif aim < l[mid_index]:
                 return two_search(l,aim,start=start,end=mid_index-1)        
             elif aim == l[mid_index]:
                 return mid_index        
             else:
                 return &#39;没有此值&#39;
    else:
         return &#39;没有此值&#39;
print(two_search(l1,9))

1	ジンシン	18

以上がPython 再帰関数、二分探索アルゴリズムの概要の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。