標準偏差の計算方法

標準偏差 (Std Dev、Standard Deviation) - 統計用語。

#データの分布の分散を測定する基準。データ値が算術平均からどの程度乖離しているかを測定するために使用されます。標準偏差が小さいほど、値は平均からの乖離が少なくなり、その逆も同様です。標準偏差の大きさは、平均に対する標準偏差の比率によって測定できます。 (推奨学習: Web フロントエンド ビデオ チュートリアル)

標準偏差は、標準偏差とも呼ばれます。標準偏差 (標準偏差) は、データからの各データの距離 (平均からの偏差) を表します。平均値は、偏差二乗和の平均の平方根であり、σ で表されます。

標準偏差は、分散の算術平方根です。標準偏差はデータセットの分散を反映しており、標準偏差が小さいほど値の平均からの乖離が少なくなり、その逆も同様です。標準偏差の大きさは、平均に対する標準偏差の比率によって測定できます。同じ平均値を持つ 2 つのデータセットは、同じ標準偏差を持たない場合があります。

計算手順

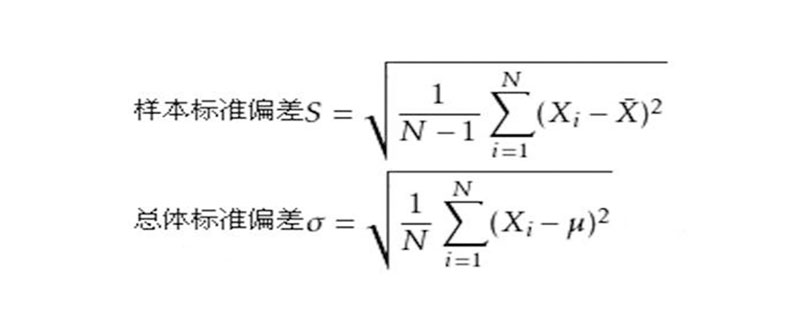
サンプル標準偏差の計算手順は次のとおりです:

ステップ 1. (各サンプル データから減算します)サンプル内のすべてのデータの平均）。

ステップ 2. ステップ 1 で取得した値の 2 乗を加算します。

ステップ 3. ステップ 2 の結果を (n - 1) で割ります (「n」はサンプル数を指します)。

ステップ 4. ステップ 3 で取得した値の平方根は、サンプリングの標準偏差です。

母集団の標準偏差を計算する手順は次のとおりです。

ステップ 1. (各サンプル データからすべての母集団データの平均を減算します)。

ステップ 2. ステップ 1 で取得した値の 2 乗を加算します。

ステップ 3. ステップ 2 の結果を n で割ります (「n」は全体の数を指します)。

ステップ 4. ステップ 3 で取得した値の平方根が全体の標準偏差です。

以上が標準偏差の計算方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。