Pythonでキャノピークラスタリングを実装する方法
- 爱喝马黛茶的安东尼オリジナル
- 2019-06-24 18:04:354137ブラウズ
Canopy アルゴリズムは、2000 年に Andrew McCallum、Kamal Nigam、Lyle Ungar によって提案されました。これは、K 平均法クラスタリング アルゴリズムと階層的クラスタリング アルゴリズムの前処理です。ご存知のとおり、kmeans の欠点の 1 つは、k 値を手動で調整する必要があることです。k 値は、後からエルボー法とシルエット係数を通じて最終的に決定できますが、これらの方法は「事後」に判断されます。 , そして、Canopy アルゴリズムの役割は、事前に大まかなクラスタリングを通じて、k-means アルゴリズムのクラスター中心とクラスター中心点の初期数を決定することです。
使用したパッケージ:
import math import random import numpy as np from datetime import datetime from pprint import pprint as p import matplotlib.pyplot as plt
1. まず、アルゴリズムに 2 次元のものをプリセットします (便利のため)後の 2 次元平面上での描画とプレゼンテーション用) データ データセット。
もちろん、高次元のデータも使用できますので、キャノピー コア アルゴリズムをクラスに記述しました。後は、任意の次元のデータを直接呼び出しで処理できます。バッチ。大量のデータ バッチを Mahout および Hadoop に移動できます。
# 随机生成500个二维[0,1)平面点 dataset = np.random.rand(500, 2)
関連する推奨事項:「Python ビデオ チュートリアル 」
2. 次に、2 つのカテゴリを生成します。クラスの属性は次のとおりです。
class Canopy:
def __init__(self, dataset):
self.dataset = dataset
self.t1 = 0
self.t2 = 0 t1とt2の初期値を設定し、サイズを決定する関数を追加します
# 设置初始阈值
def setThreshold(self, t1, t2):
if t1 > t2:
self.t1 = t1
self.t2 = t2
else:
print('t1 needs to be larger than t2!')3. 距離計算、各中心点間の距離計算方法はユークリッド距離です私が使う。
#使用欧式距离进行距离的计算
def euclideanDistance(self, vec1, vec2):
return math.sqrt(((vec1 - vec2)**2).sum())4. 次に、データセットの長さに応じてデータセットから添字をランダムに選択する関数を作成します
# 根据当前dataset的长度随机选择一个下标
def getRandIndex(self):
return random.randint(0, len(self.dataset) - 1)5. コア アルゴリズム
def clustering(self):
if self.t1 == 0:
print('Please set the threshold.')
else:
canopies = [] # 用于存放最终归类结果
while len(self.dataset) != 0:
rand_index = self.getRandIndex()
current_center = self.dataset[rand_index] # 随机获取一个中心点，定为P点
current_center_list = [] # 初始化P点的canopy类容器
delete_list = [] # 初始化P点的删除容器
self.dataset = np.delete(
self.dataset, rand_index, 0) # 删除随机选择的中心点P
for datum_j in range(len(self.dataset)):
datum = self.dataset[datum_j]
distance = self.euclideanDistance(
current_center, datum) # 计算选取的中心点P到每个点之间的距离
if distance < self.t1:
# 若距离小于t1，则将点归入P点的canopy类
current_center_list.append(datum)
if distance < self.t2:
delete_list.append(datum_j) # 若小于t2则归入删除容器
# 根据删除容器的下标，将元素从数据集中删除
self.dataset = np.delete(self.dataset, delete_list, 0)
canopies.append((current_center, current_center_list))
return canopies後続のデータ視覚化を容易にするために、ここで定義するキャノピーは配列ですが、もちろん dict も使用できます。
6.main() 関数
def main():
t1 = 0.6
t2 = 0.4
gc = Canopy(dataset)
gc.setThreshold(t1, t2)
canopies = gc.clustering()
print('Get %s initial centers.' % len(canopies))
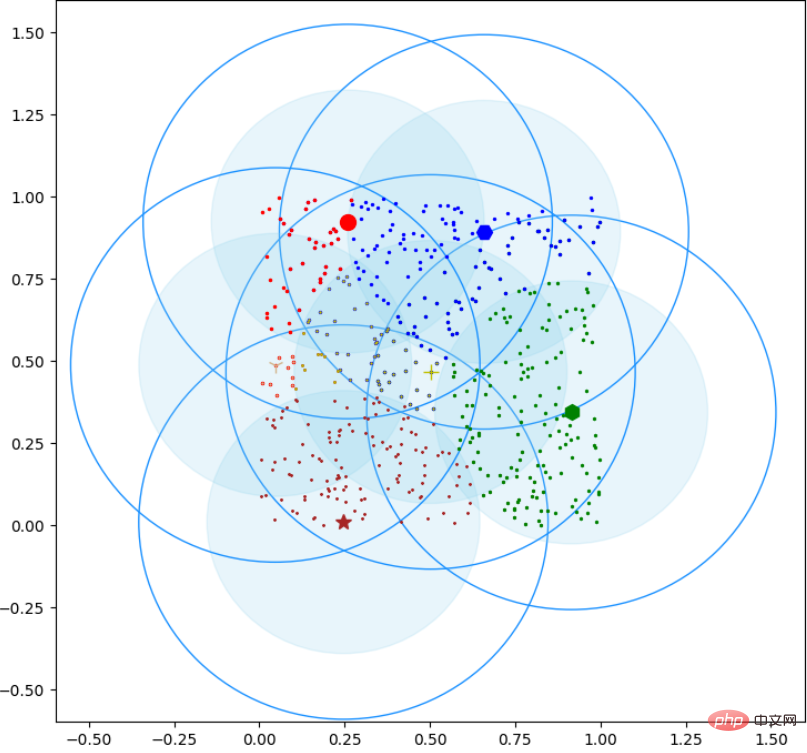
#showCanopy(canopies, dataset, t1, t2)キャノピー クラスタリング視覚化コード
def showCanopy(canopies, dataset, t1, t2):
fig = plt.figure()
sc = fig.add_subplot(111)
colors = ['brown', 'green', 'blue', 'y', 'r', 'tan', 'dodgerblue', 'deeppink', 'orangered', 'peru', 'blue', 'y', 'r', 'gold', 'dimgray', 'darkorange', 'peru', 'blue', 'y', 'r', 'cyan', 'tan', 'orchid', 'peru', 'blue', 'y', 'r', 'sienna']
markers = ['*', 'h', 'H', '+', 'o', '1', '2', '3', ',', 'v', 'H', '+', '1', '2', '^', '<', '>', '.', '4', 'H', '+', '1', '2', 's', 'p', 'x', 'D', 'd', '|', '_'] for i in range(len(canopies)):
canopy = canopies[i]
center = canopy[0]
components = canopy[1]
sc.plot(center[0], center[1], marker=markers[i],
color=colors[i], markersize=10)
t1_circle = plt.Circle(
xy=(center[0], center[1]), radius=t1, color='dodgerblue', fill=False)
t2_circle = plt.Circle(
xy=(center[0], center[1]), radius=t2, color='skyblue', alpha=0.2)
sc.add_artist(t1_circle)
sc.add_artist(t2_circle) for component in components:
sc.plot(component[0], component[1],
marker=markers[i], color=colors[i], markersize=1.5)
maxvalue = np.amax(dataset)
minvalue = np.amin(dataset)
plt.xlim(minvalue - t1, maxvalue + t1)
plt.ylim(minvalue - t1, maxvalue + t1)
plt.show()レンダリングは次のとおりです:
以上がPythonでキャノピークラスタリングを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。