時間計算量を理解するのに役立つデータ構造の図のセット

この記事では、時間計算量とは何かを簡単に理解できるように、一連の画像を使用しています。興味深く、鮮明で、一定の学習価値があります。興味のある友人は、来て調べてください。 。

#時間計算量の意味

時間計算量とは正確には何ですか?あるシーンを想像してみましょう: ある日、シャオ ホイとダー ファンは同時に会社に入社しました...

1 日後、シャオ ホイとダー ファンはそれぞれ出産しました。コード、両端のコードによって実装される機能は類似しています。 Dahuang のコードは 1 回の実行に 100 ミリ秒かかり、5 MB のメモリを占有します。 Xiao Hui のコードは 1 回の実行に 100 秒かかり、500 MB のメモリを消費します。したがって...

#コードの品質の測定には 2 つの非常に重要な指標が含まれていることがわかります。

1. 実行時間;

2. 占有スペース。

基本操作実行数

コードの基本操作の実行数について、人生の 4 つのシーンを比喩として使用します。 1 :

シャオ ホイに 10 インチのパンをあげます。シャオ ホイは 3 日ごとに 1 インチを食べます。パンを全部食べるには何日かかりますか?

答えは当然、3 X 10 = 30 日です。

パンの長さが N インチだったらどうなるでしょうか?

現時点でパンをすべて食べるには、3 X n = 3n 日かかります。

関数を使用してこの相対時間を表す場合、T(n) = 3n として記録できます。

シナリオ 2:

Xiao Hui に 16 インチのパンを与えます。Xiao Hui は 5 日ごとに残りの長さのパンの半分を食べます。最初は 8 インチを食べ、その後 8 インチを食べます。 2回目は4インチ、3回目は2インチを食べました...では、シャオ・ホイが1インチのパンだけを食べるには何日かかりますか?

この質問を翻訳すると、数値 16 を 2 で割り続けると、結果は何回 1 になりますか?これには数学の対数が関係しており、底 2 の 16 の対数は log16 と略すことができます。

したがって、わずか 1 インチのパンを食べるには、5 X log16 = 5 X 4 = 20 日かかります。 パンの長さが N インチだったらどうなるでしょうか?

5 X logn = 5logn 日が必要で、T(n) = 5logn として記録されます。

シナリオ 3:

Xiao Hui に 10 インチのパンと鶏ドラムスティックを 1 つ与えます。Xiao Hui は 2 日に 1 本のドラムスティックを食べます。それでは、シャオ・ホイが鶏もも肉を丸ごと食べるには何日かかるでしょうか?

#答えは当然 2 日です。鶏の足を食べるだけなので、10インチのパンとは関係ありません。 パンの長さが N インチだったらどうなるでしょうか?

パンがどれだけ長くても、鶏の足を食べるのにかかる時間は依然として 2 日であり、T(n) = 2 として記録されます。

シナリオ 4: Xiao Hui に 10 インチのパンを与えます。Xiao Hui が最初の 1 インチを食べるのに 1 日、2 インチを食べるのに 2 日、そして 2 インチを食べるのに 2 日かかります。 3 インチ。1 インチを食べるのに 3 日かかります。1 インチ増えるごとに、さらに 1 日かかります。それで、シャオ・フイがパンを全部食べるには何日かかりますか?

答えは、1 から 10 までの合計、つまり 55 日です。

パンの長さが N インチだったらどうなるでしょうか?

この時点でパンを全部食べるには、1 2 3... n-1 n = (1 n)*n/2 = 0.5n^2 0.5n かかります。

T(n) = 0.5n^2 0.5n として記録されます。

上で話したのは相対的な食事時間の話ですが、この考え方はプログラムの基本演算回数の統計にも当てはまります。ここで説明した 4 つのシナリオは、プログラム内で最も一般的な 4 つの実行方法に対応しています。

シナリオ 1: T(n) = 3n、実行数は線形です。

void eat1(int n){
    for(int i=0; i<n; i++){;
        System.out.println("等待一天");
        System.out.println("等待一天");
        System.out.println("吃一寸面包");
    }
}
vo

シナリオ 2: T(n) = 5logn、実行数は対数です。

void eat2(int n){
   for(int i=1; i<n; i*=2){
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("吃一半面包");
   }
}

シナリオ 3: T(n) = 2、実行数は一定です。

void eat3(int n){
   System.out.println("等待一天");
   System.out.println("吃一个鸡腿");
}

シナリオ 4: T(n) = 0.5n^2 0.5n、実行数は多項式です。

void eat4(int n){
   for(int i=0; i<n; i++){
       for(int j=0; j<i; j++){
           System.out.println("等待一天");
       }
       System.out.println("吃一寸面包");
   }
}

漸近的時間計算量

基本操作の実行回数の関数 T(n) を使用して、コードの実行時間を分析および比較できますか?まだいくつかの困難があります。

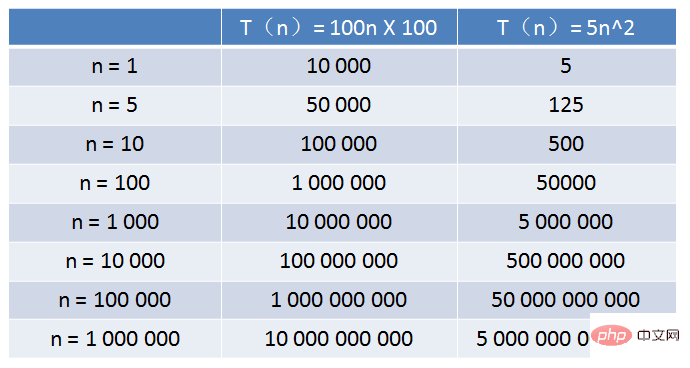
たとえば、アルゴリズム A の相対時間は T(n) = 100n、アルゴリズム B の相対時間は T(n) = 5n^2 です。実行時間はどちらの方が長いでしょうか?これは n の値によって異なります。

そこで、現時点では、漸近時間計算量 (asymptotic time complectiy) という概念があり、正式な定義は次のとおりです。 n が無限大に近づくとき、 T(n)/f(n) の限界値が 0 に等しくない定数であるとき、f(n) は T(n) と同じ桁の大きさの関数であると言われます。 。

T(n) = O(f(n)) と表され、O(f(n)) は、アルゴリズムの漸近時間計算量、または略して時間計算量と呼ばれます。

漸近的時間計算量は大文字の O で表されるため、ビッグ O 表記法とも呼ばれます。

時間計算量をどのように導き出すか?いくつかの原則があります:

実行時間が一定の大きさである場合、定数 1 を使用してそれを表します;
2. keep the time 関数 最上位項;

3. 最上位項が存在する場合、最上位項の前の係数は省略されます。

先ほどの4つのシーンを振り返ってみましょう。

シナリオ 1:

T(n) = 3n

最上位項は 3n で、係数 3 と変換は省略されます。時間の複雑さは次のとおりです:

T(n) = O(n)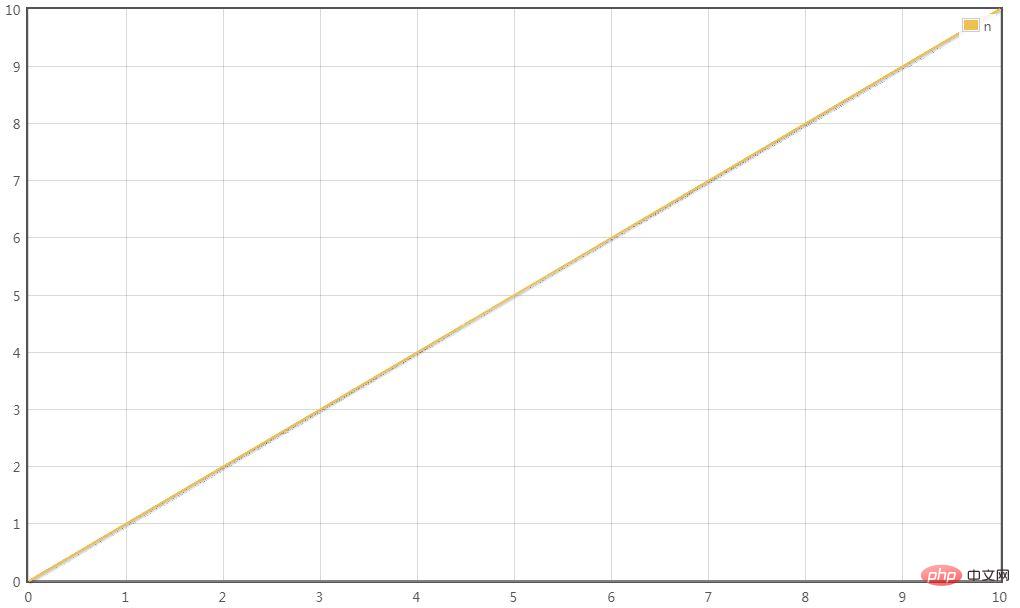

## シナリオ 2:

T (n) = 5logn

最高次項は 5logn で、係数 5 を省略すると、変換の時間計算量は次のようになります:

T(n) = O(logn)

シナリオ 3:

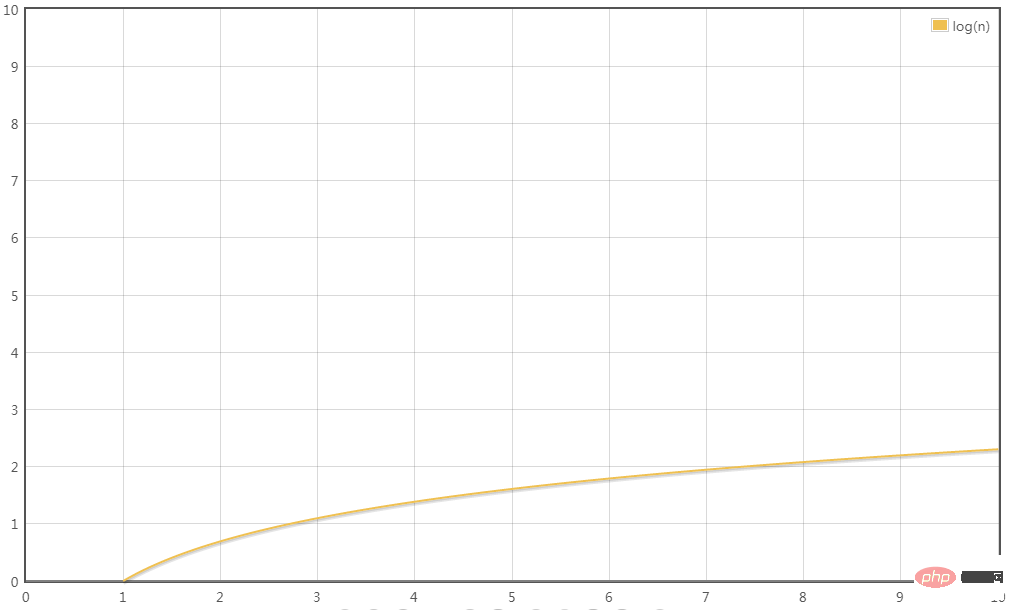
T(n) = 2

は一定の大きさのみであり、変換の時間計算量は一定ですは:

T(n) = O(1)

シナリオ 4:

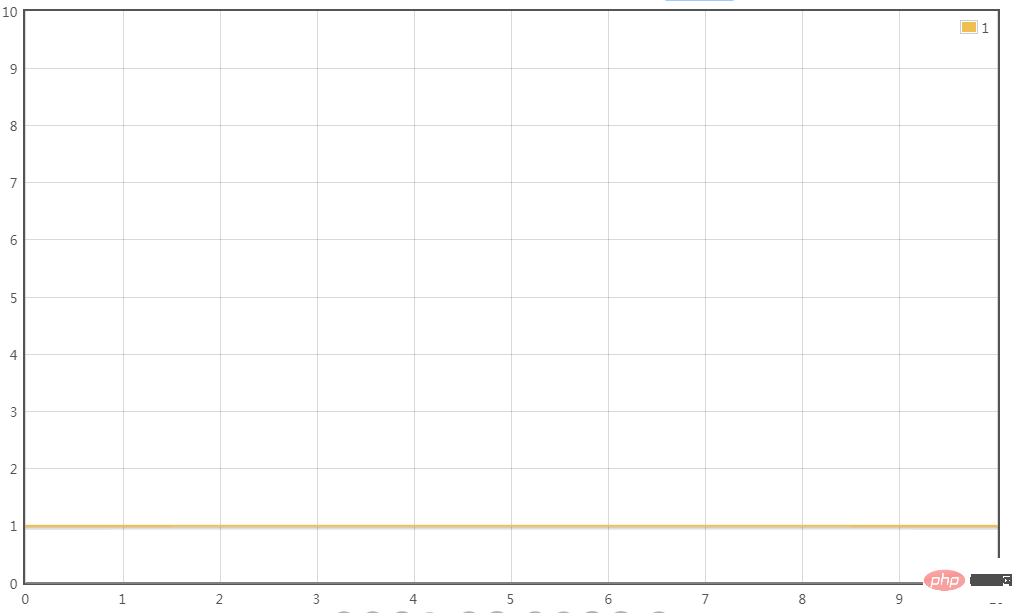
T(n ) = 0.5n^ 2 0.5n

最高次項は 0.5n^2 で、係数 0.5 を省略すると、変換の時間計算量は次のようになります:

T(n) = O( n^2)

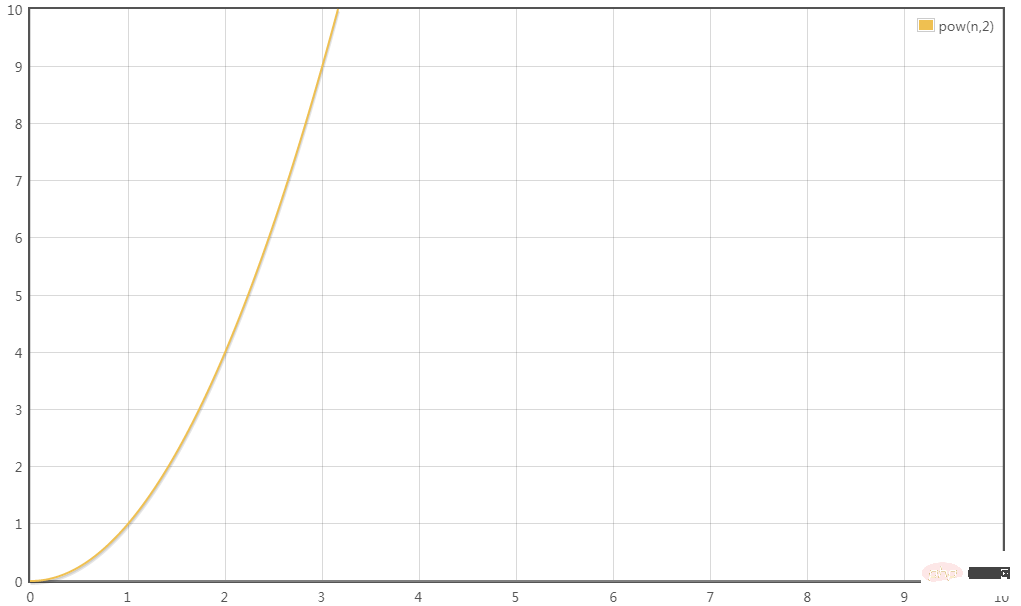これら 4 つの時間の複雑さのうち、時間がかかるのはどれで、時間を節約できるのはどれですか?少し考えれば、次のような結論に達することができます。

O(1)

プログラミングの世界 さまざまなアルゴリズムがあります。上記の 4 つのシナリオに加えて、

O(nlogn)、O(n^3)、O(m* など、さまざまな形の時間計算量があります。 n ), O(2^n), O(n!)

将来、私たちがコードの海を旅するとき、上記のような時間計算量のアルゴリズムに遭遇し続けるでしょう。

# 時間の複雑さの大きな違い

栗をあげましょう:

アルゴリズム A の相対時間スケールは T(n) = 100n、時間計算量は O(n)です

アルゴリズム B の相対時間スケールは T(n) = 5n^2、時間計算量は O(n^2)です。

アルゴリズム A はシャオ ホイの家にある古いコンピューターで実行され、アルゴリズム B は特定のスーパーコンピューターで実行されます。動作速度は古いコンピュータの 100 倍です。

それでは、入力サイズ n が増加すると、2 つのアルゴリズムのどちらがより速く実行されるでしょうか?

表から、n の値が非常に小さい場合、アルゴリズム A の実行時間はアルゴリズム B の実行時間よりもはるかに長くなることがわかります。 n が約 1000 に達すると、アルゴリズム A とアルゴリズム B の実行時間は近くなります。n の値がますます大きくなり、10 万、100 万に達すると、アルゴリズム A の利点が現れ始めますが、アルゴリズム B は遅くなりますそして遅くなり、その差はますます明らかになっていきます。

これは、時間計算量の違いによって生じる違いです。

さらに技術的なチュートリアルを知りたい場合は、

PHP 中国語 Web サイト に注目してください。

以上が時間計算量を理解するのに役立つデータ構造の図のセットの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。