ホームページ >バックエンド開発 >Python チュートリアル >Python を使用して円周率を計算する方法 (コード例)
Python を使用して円周率を計算する方法 (コード例)
- 不言転載
- 2019-03-18 09:22:1924598ブラウズ
この記事の内容はPythonを使って円周率を計算する方法(コード例)です、ある程度の参考値があるので困っている友達は参考にしていただければ幸いです。
1. π の概要
π の概要
Pi はギリシャ文字 π (pài と発音) で表され、定数 ( 3.141592654 にほぼ等しい)、これは円の円周と直径の比を表します。これは、無限に繰り返されない 10 進数であり、日常生活では、近似計算の円周率を表すために通常 3.14 が使用されます。
πの解法
1965年、英国の数学者ジョン・ウォリスは数学モノグラフを出版し、その中で公式を導出し、円周率が分数の積である無限大に等しいことを発見しました。
2015 年、ロチェスター大学の科学者は、水素原子のエネルギー準位の量子力学的計算で同じ円周率の公式を発見しました。
2019 年 3 月 14 日、Google は円周率が小数点以下の桁数 31.4 兆桁に達したと発表しました。
ここでは私が解くのに「良い」と思った公式を使用します。計算結果は比較的正確なので良いのですが、計算処理に時間がかかります。一緒に学びましょう~~
2. πの近似計算
1. 計算式
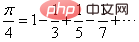
2. 方法説明
の右辺の分子方程式はすべて 1 で、分母は最初の項目から始まる増加数列で、奇数番目の項の符号は正、偶数番目の項の符号は負です。式の右辺の分母が大きいほど、または小さいほど、円周率の計算値はより正確になります。言い換えると、式の右辺の項が多いほど、計算値はより正確になります。
3. コード実装 (Python)
from math import fabs #导入数学模块
from time import perf_counter #导入时间模块
def Bar(i): #动态文本条
N = pow(10,level)
a = int((i/N)*50)
b = 50 - a
Y , N = '*' * a , '.' * b
print("\r计算中:{:3.0f}% [{}->{}] {:.2f}s"
.format(2*a,Y,N,perf_counter()),end='')
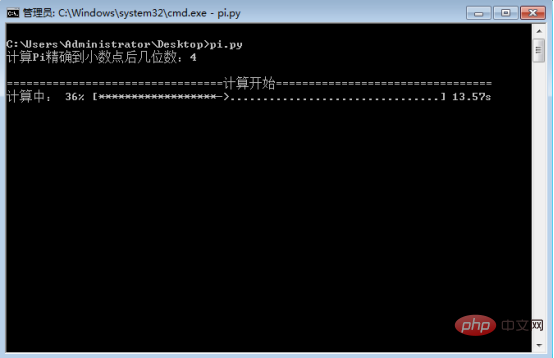
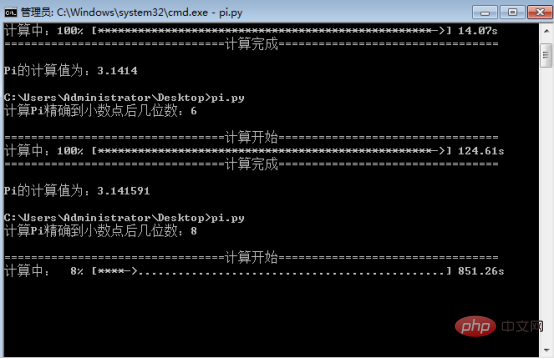
level = eval(input('计算Pi精确到小数点后几位数:'))
print('\n{:=^70}'.format('计算开始'))
a,b,pi,tmp = 1,1,0,1
i = 0
'''
a 分子 | b 分母 | pi 圆周率
tmp 存储a/b的值 | i 执行进度
'''
perf_counter() #开始计时
while (fabs(tmp) >= pow(10,-level)): #计算Pi
pi += tmp
b += 2
a = -a
tmp = a/b
i += 2
Bar(i) #调用函数,实时显示计算进度
print('\n{:=^70}'.format('计算完成'))
print('\nPi的计算值为:{}'.format(round(pi*4,level))) #输出计算结果4. 画像の例

以上がPython を使用して円周率を計算する方法 (コード例)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

