ホームページ >ウェブフロントエンド >jsチュートリアル >浮動小数点数の表現範囲
浮動小数点数の表現範囲
- 清浅オリジナル
- 2019-03-08 15:57:2237829ブラウズ
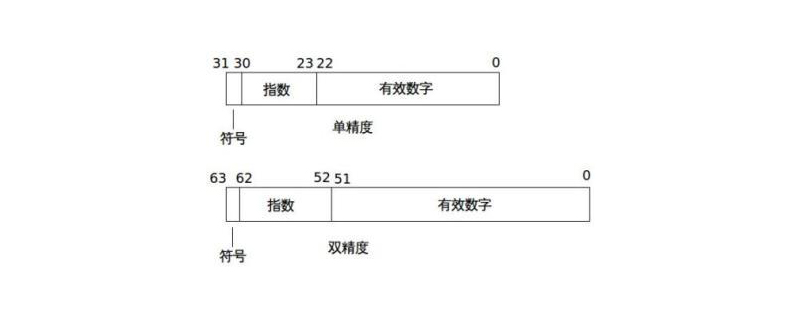
浮動小数点数は、記号、指数、仮数の 3 つの部分で構成されます。浮動小数点数は、単精度浮動小数点数と倍精度浮動小数点数に分けられます。単精度浮動小数点数の範囲は -3.4E38 ~ 3.4E38、倍精度浮動小数点数の範囲は -1.79E 308 ~ 1.79E 308
[推奨コース: JavaScript チュートリアル]
浮動小数点数表現
浮動小数点数 (浮動小数点数) は、符号、指数という 3 つの基本コンポーネントで構成されます。そして仮数部。浮動小数点数は通常、次の形式で表すことができます:
| P | M |
| P | M | 式を表します | オフセット | ||
| 1 (31 位) | 8 (30 位から 23 位) | 23 (22 位から 0 位) | (-1)^S*2 (P-127) *1.M | 127 | |
| 1(63ビット目) | 11 (62 ~ 52 ビット) | 52 (桁 51 ~ 0) | (-1)^S*2(P-1023)*1.M | 1023 |
| Binary (2 進数) | Decimal(10 進数) | |
| 単精度浮動小数点数 | ± (2-2^-23) × 2127 | ~ ± 10^38.53 |
| 倍精度浮動小数点数 | ± (2-2^-52) × 21023 | ~ ± 10^ 308.25 |
浮動小数点数の表現には一定の範囲があり、その範囲を超えるとオーバーフロー(Flow)が発生します。一般に絶対値の最大値より大きいデータをオーバーフロー(Overflow)、絶対値の最大値より小さいデータをオーバーフロー(Overflow)と呼びます。絶対値が最も小さいことをアンダーフロー(Underflow)と呼びます。
浮動小数点数の表現規則
単精度浮動小数点数と倍精度浮動小数点数は両方とも IEEE 754 標準で定義されています。例:
1. P=0、M=0 の場合、0 を意味します。
2. P=255、M=0の場合は無限大を意味し、正の無限大か負の無限大かを判断するために符号ビットが使用されます。
3. P=255かつM≠0の場合、NaN(Not a Number、非数)を意味します。
非標準の浮動小数点数
絶対値が極端に小さい 2 つの浮動小数点数を減算すると、その差の指数が許容範囲を超える場合があり、最終的にはほぼ 0 になるだけです。このような問題を解決するために、IEEE 標準は非正規化浮動小数点数を導入しました。これは、浮動小数点数の指数が許容される最小指数値である場合、仮数を正規化する必要がないことを規定しています。非標準浮動小数点数では、仮数ビットの暗黙の制限がなくなり、絶対値が小さい浮動小数点数を格納できるようになります。さらに、暗黙の仮数フィールドによる制限がなくなるため、保存できる浮動小数点数間のすべての差分も保存できるため、極度に小さい差分に関する上記の問題は存在しません。
IEEE 754 標準の定義によれば、正規浮動小数点数と非正規浮動小数点数の表現範囲は次の表のように要約できます。
| #非正規浮動小数点数 | #10 進近似範囲##単精度浮動小数点数 | ||
| ± 2^-126 から (2-2^-23)*2^127 | ± ~10^-44.85 ~ ~10^38.53 | 倍精度浮動小数点数 | |
| ± 2^-1022 から (2-2^-52)*2^1023 | ± ~10^-323.3 から ~10^308.3 | #IEEE 754 に関連する規格 |
要約: 以上がこの記事の全内容です。皆様のお役に立てれば幸いです。
以上が浮動小数点数の表現範囲の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

