Python はモンテカルロ法を実装します (コード例)

この記事の内容は、Python でのモンテカルロ法 (コード例) の実装に関するもので、一定の参考価値がありますので、困っている方は参考にしていただければ幸いです。

モンテカルロ法は、フォン・ノイマンとウラムによって提案された統計シミュレーション手法です。多数の乱数の下で、確率推定の結果によると、ランダムなデータが多いほど、結果は次のようになります。より正確な。以下では、Python を使用してモンテカルロ法を実装します。

1. まず、円周率の簡単な近似計算を行います。このプロセスでは乱数を使用する必要があるため、最初に import numpy as np を使用して numpy ライブラリをインポートする必要があります。

2. コードの実装:

import numpy as np

total = 8000000
count = 0

for i in range(total):
    x = np.random.rand()
    y = np.random.rand()
    dis = (x**2+y**2)**0.5
    if dis <p>3. 上記のプログラムでは、得られる結果がより正確になるように、配信に 8000000 個の乱数を使用していますが、ある程度の時間がかかります。プログラムの実行にかかる時間です。最終結果は次のとおりです。</p><p><span class="img-wrap"><img src="https://img.php.cn//upload/image/549/675/172/1547436392667253.png" title="1547436392667253.png" alt="Python はモンテカルロ法を実装します (コード例)"></span></p><p></p>4 簡単なアプリケーションを実行してみましょう。下の図は私が描いたものです。描画ツールでランダムに描画し、モンテカルロ法を使用して画像内の黒い部分の面積を推定できます。 <p   style="max-width:90%"><span class="img-wrap"><img src="https://img.php.cn//upload/image/583/174/740/1547436406520588.png" title="1547436406520588.png" alt="Python はモンテカルロ法を実装します (コード例)"></span></p><p></p>5. 上のグラフは不規則ですが、大量の乱数を投げると乱数が現れるということだけを理解する必要があります。黒い部分の確率を計算し、その合計面積を乗じて黒い部分の面積を推定します。黒のRGBコードは(0,0,0)であることがわかっているので、RGBコードが(0,0,0)である場合の乱数の確率を計算する必要があります。 <p></p>6. コード実装: <p></p><pre class="brush:php;toolbar:false">from PIL import Image
import numpy as np

im = Image.open("C:/Users/21974/Desktop/handwrite2.PNG")
total = 9000000
count = 0
defin = 0
width = im.size[0]
height = im.size[1]

for i in range(total):    #用蒙特卡罗方法获得估计值
    x = np.random.randint(0, width-1)
    y = np.random.randint(0, height-1)
    k = im.getpixel((x, y))
    if k[0]+k[1]+k[2] == 0:
        count += 1
print(int(width*height*count/total))

for i in range(width):    #用遍历获得准确值
    for j in range(height):
        k = im.getpixel((i, j))
        if k[0] + k[1] + k[2] == 0:
            defin += 1
print(defin)

上記のコードは 2 つの部分に分けることができ、最初の for にモンテカルロ法で求めた面積の推定値が続き、2 番目の部分にモンテカルロ法による面積の推定値が続きます。 for の後に「It は、すべてのピクセルを走査することによって得られる領域の正確な値です」が続き、2 つの出力を比較します。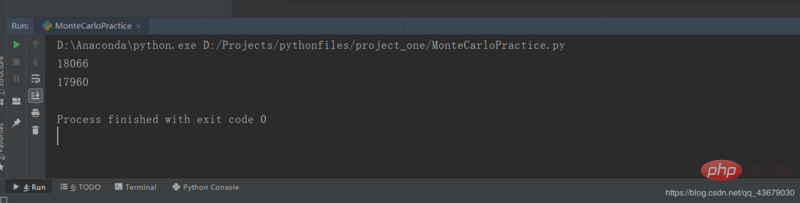

上記のプログラムでは 9,000,000 個の乱数を使用しましたが、2 つの出力結果に大きな違いがないことがわかります。

###

以上がPython はモンテカルロ法を実装します (コード例)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。