JavaScript のバイナリ ツリー (バイナリ ヒープ) の概要 (コード例)

この記事では、JavaScript のバイナリ ツリー (バイナリ ヒープ) についての紹介 (コード例) を紹介します。必要な方は参考にしていただければ幸いです。

バイナリ ツリー

バイナリ ツリー (Binary Tree) は、各ノードが最大 2 つの分岐ノードを持つというツリー構造です。ルートノード、ブランチノード、リーフノードで構成されます。各ブランチ ノードはサブツリーと呼ばれることがよくあります。

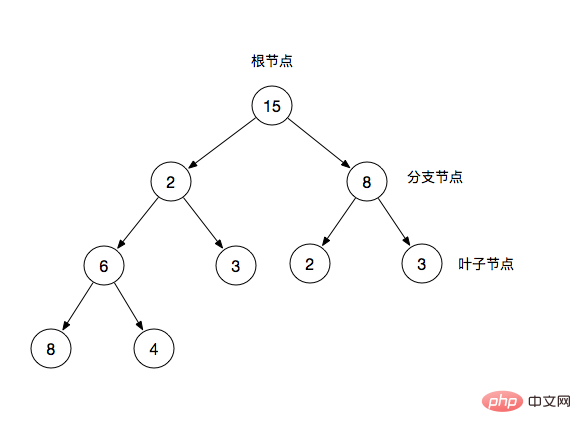
• ルート ノード: バイナリ ツリーの最上位ノード

• ブランチノード: ルート ノードに加えてリーフ ノードがあります

• リーフ ノード: それ自体を除き、他の子ノードはありません

共通用語

二分木では、親ノードと子ノードを使って説明することがよくあります。たとえば、図の 2 は 6 と 3 の親ノードであり、その逆は 6 です。と 3 は 2 の子ノードです

バイナリ ツリーの 3 つのプロパティ

1. ##バイナリ ツリーの i 番目のレベルには、次のものがあります。ほとんどの 2^i-1 ノード

• i=1 の場合、ルート ノードは 1 つだけ、2^(i-1) = 2^0 = 1

深さ k の二分木は最大 2^k-1 個のノードがあります

• i=2, 2 の場合^k-1 = 2^2 - 1 = 3 ノード

任意の二分木 T について、要約点の数が n0 で、次数 2 のノードの数がある場合(サブツリーの数は 2) は n2、n0=n2 1

ツリーとバイナリ ツリーの 3 つの主な違い

• ツリーのノード数は少なくとも 1 ですが、バイナリ ツリーのノード数は 0 まで可能です

• ノードの最大次数 (ノード数) に制限はありません。二分木のノードの最大次数は 2

• 木のノード間には左右の区別はありませんが、二分木のノードには左右の区別がありません。

#バイナリ ツリーの分類

バイナリ ツリーは完全バイナリ ツリーと完全バイナリ ツリーに分類されます

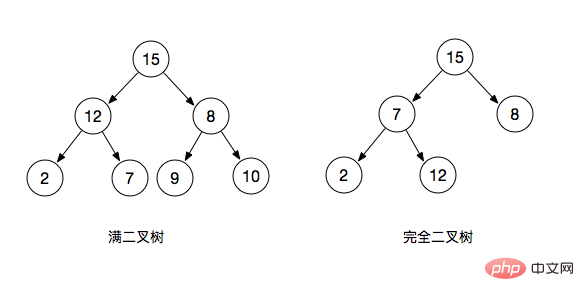
完全なバイナリ ツリー: 深さ k および 2^k - 1 ノードを持つバイナリ ツリーは、完全なバイナリ ツリーと呼ばれます。
完全なバイナリ ツリー: 完全なバイナリ ツリーは、完全なバイナリ ツリーの左側を指します。最後の層 いっぱいです。右側はいっぱいであるかいっぱいではありません。残りのレベルは完全な二分木と呼ばれます (完全な二分木は完全な二分木でもあります)

• 。

バイナリ ツリーの配列表現

配列を使用して、バイナリ ツリーの構造を表現します。次の図に示すように、完全なバイナリ ツリーでは、ルート ノードから上から下、左から右に配列されます。上の図から、配列で表される完全なバイナリ ツリーには次のプロパティがあることが分析できます。

left = Index * 2 1、たとえば、ルート ノードの添字は次のとおりです。 0 の場合、左ノードの値は添字 array[0*2 1]=1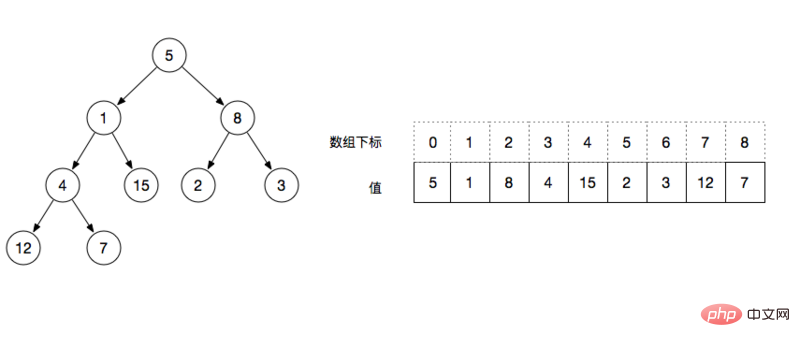

right = Index * 2 2 になります。たとえば、ルート ノードの添字は次のようになります。 0 の場合、右側のノードの値は添字になります。 array[0*2 2]=2

• Ordinal>= Floor(N/2) はすべてリーフ ノードです。次に例を示します。 Floor(9/2) = 4 の場合、添え字 4 から始まる値はすべてリーフ ノードです

• Binary Heap
  バイナリ ヒープの構造を表します配列で表される完全なバイナリ ツリーによって表現されますが、バイナリ ヒープは次のプロパティを満たす必要があります:

• バイナリ ヒープの親ノードのキー値は常に​​大きくなります。任意の子ノードのキー値以上（以下）

親ノードのキー値以上（以下）の場合) 各子ノードのキー値。

最大ヒープ (最小ヒープ)

• と呼ばれます。

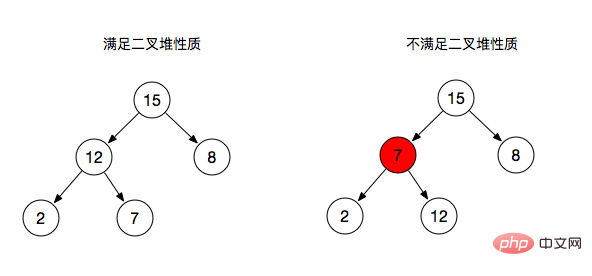  上の図からわかるように:

  左の図: 親ノードは常にそのノード以上です。子ノード なので、バイナリ ヒープのプロパティは満たされます。

右の図: 2 と 12 の親ノードであるブランチ ノード 7 は、そのプロパティ (以上または子ノードに等しい)。

• バイナリ ヒープの主な操作

• insert: ノードの挿入

delete: ノード # の削除

##max-hepify: ブランチ ノード ヒープのプロパティを調整します
rebuildHeap: バイナリ ヒープ全体を再構築します
sort: ソート
バイナリ ヒープの初期化

• 上記の簡単な説明から、バイナリ ヒープの初期化は単なる配列であることがわかります。

• 配列構造を初期化する

• 配列の長さを保存する

    class Heap{
        constructor(arr){
            this.data = [...arr];
            this.size = this.data.length;
        }
    }

max-heapify 最大ヒープ操作

max-heapify は、条件を満たさない各項目を変換することです。最大ヒープのプロパティ ブランチ ノードを調整する操作。

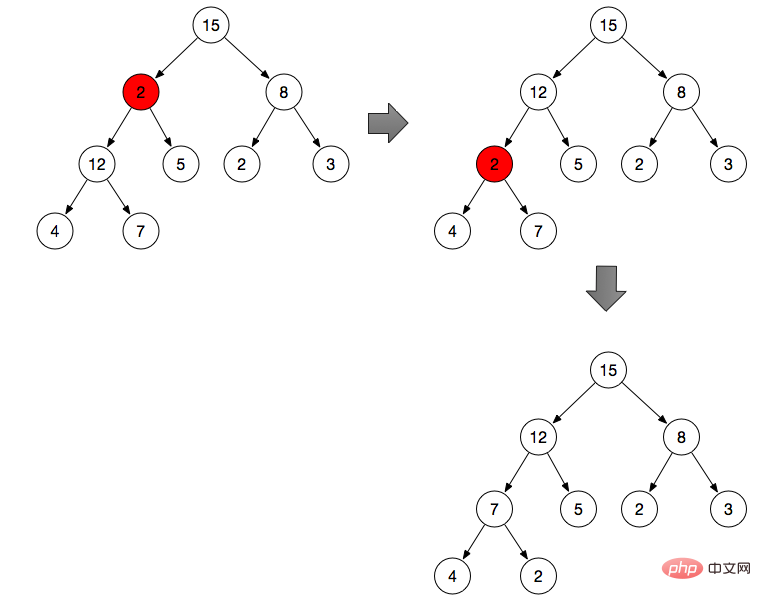
上に示すように:

1. ブランチ ノード 2 を調整します (ブランチ ノード 2 はプロパティを満たしていません) )

• デフォルトでは、ブランチ ノードが最大値です。

2 を左と比較してください。 2、12からの右の分岐、5の最大値を見つけて、位置を2と交換します

• 上記のバイナリヒープのプロパティに従って、左側のノードを取得しますと分岐ノード 2 の右側のノードをそれぞれ

• 3 つのノードを比較し、最大値の添え字 max を取得します

• ノード自体が最大値、操作を停止します

• 最大ノードを親ノードと交換します

##ステップ 2 の操作を繰り返し、 2、4、7 の最大値を取得し、2 に交換します。

• Recursion

    maxHeapify(i) {
        let max = i;
        
        if(i >= this.size){
            return;
        }
        // 当前序号的左节点
        const l = i * 2 + 1;
        // 当前需要的右节点
        const r = i * 2 + 2;
        
        // 求当前节点与其左右节点三者中的最大值
        if(l  this.data[max]){
            max = l;
        }
        if(r  this.data[max]){
            max = r;
        }
        
        // 最终max节点是其本身,则已经满足最大堆性质，停止操作
        if(max === i) {
            return;
        }
        
        // 父节点与最大值节点做交换
        const t = this.data[i];
        this.data[i] = this.data[max];
        this.data[max] = t;
        
        // 递归向下继续执行
        return this.maxHeapify(max);
    }

ヒープの再構築

新しく初期化されたヒープは配列で表されますが、現時点では最大ヒープまたは最小ヒープのプロパティを満たしていない可能性があることがわかります。現時点では、ヒープ全体を何に構築する必要があるかもしれません。私たちが望んでいます。

上記では max-heapify 操作を実行しましたが、max-heapify は特定のブランチ ノードのみを調整します。ヒープ全体を最大ヒープに構築するには、すべてのブランチ ノードで max-heapify 操作を実行する必要があります。以下の図では、4 つのブランチ ノード 12、3、2、および 15 に対して max-hepify 操作を順番に実行する必要があります

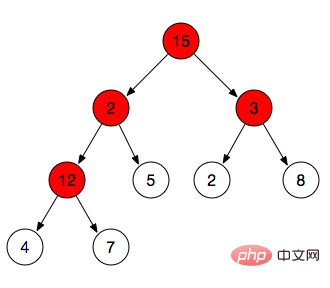#具体的な手順:

すべてのブランチ ノードの検索: 前述のヒープのプロパティでは、リーフ ノードのシリアル番号 >= Math.floor(n/2) であるため、これはMath.floor(n/2) のシリアル番号 これらは調整する必要があるすべてのノードです。
たとえば、中央に示されている配列は [15,2,3,12,5,2,8,4,7] => Math.floor (9/2 )=4 => インデックスが 4 未満のものは 15、2、3、12 (調整が必要なノード) で、5、2、8、4、7 はリーフ ノードです。
#見つかったすべてのノードで maxHeapify 操作を実行します

•     rebuildHeap(){
          // 叶子节点
          const L = Math.floor(this.size / 2);
          for(let i = L - 1; i>=0; i--){
              this,maxHeapify(i);
          }
      }

  最大ヒープ ソート

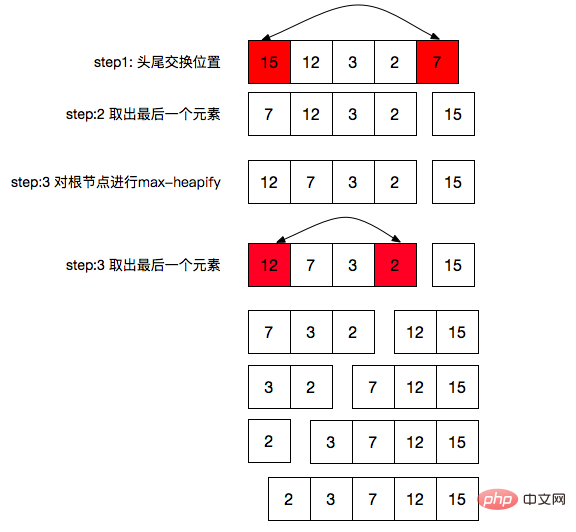上図に示す最大ヒープのソート:

最初と最後の位置を交換します

• 最後の要素を変更します。ヒープのサイズ 1 に相当する要素がヒープから取り出されます。

• 次に、次のルート ノードで max-heapify 操作を実行します。ヒープ

• #繰り返し 上記の 3 つのステップで、size=0 であることがわかります (この境界条件は max-heapify 関数ですでに実行済みです)

•     sort() {
          for(let i = this.size - 1; i > 0; i--){
              swap(this.data, 0, i);
              this.size--;
              this.maxHeapify(0);
          }
      }

  挿入と削除

この削除の挿入と削除は比較的単純で、配列の挿入と削除の操作です。

end

• ヒープ長 1

• 挿入後もまだ最大ヒープであるかどうかを確認します

• そうでない場合は、ヒープを再構築します

•   insert(key) {
      this.data[this.size] = key;
      this.size++
      if (this.isHeap()) {
        return;
      }
      this.rebuildHeap();
    }

配列内の要素を削除します

• ヒープ長-1

• ヒープであるかどうかを判断します

• そうでない場合は、ヒープを再構築します

•   delete(index) {
      if (index >= this.size) {
        return;
      }
      this.data.splice(index, 1);
      this.size--;
      if (this.isHeap()) {
        return;
      }
      this.rebuildHeap();
    }

  完全なコード

/**
 * 最大堆
 */

function left(i) {
  return i * 2 + 1;
}

function right(i) {
  return i * 2 + 2;
}

function swap(A, i, j) {
  const t = A[i];
  A[i] = A[j];
  A[j] = t;
}

class Heap {
  constructor(arr) {
    this.data = [...arr];
    this.size = this.data.length;
  }

  /**
   * 重构堆
   */
  rebuildHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i--) {
      this.maxHeapify(i);
    }
  }

  isHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i++) {
      const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
      const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;

      const max = Math.max(this.data[i], l, r);

      if (max !== this.data[i]) {
        return false;
      }
      return true;
    }
  }

  sort() {
    for (let i = this.size - 1; i > 0; i--) {
      swap(this.data, 0, i);
      this.size--;
      this.maxHeapify(0);
    }
  }

  insert(key) {
    this.data[this.size++] = key;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  /**
   * 堆的其他地方都满足性质
   * 唯独跟节点，重构堆性质
   * @param {*} i
   */
  maxHeapify(i) {
    let max = i;

    if (i >= this.size) {
      return;
    }

    // 求左右节点中较大的序号
    const l = left(i);
    const r = right(i);
    if (l  this.data[max]) {
      max = l;
    }

    if (r  this.data[max]) {
      max = r;
    }

    // 如果当前节点最大，已经是最大堆
    if (max === i) {
      return;
    }

    swap(this.data, i, max);

    // 递归向下继续执行
    return this.maxHeapify(max);
  }
}

module.exports = Heap;

概要

ヒープはここです、ヒープはです バイナリ ツリーは比較的単純で、並べ替えキューや優先キューによく使用されます。ヒープの中核は、max-heapify 操作とヒープの 3 つのプロパティです。

以上がJavaScript のバイナリ ツリー (バイナリ ヒープ) の概要 (コード例)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。