ホームページ >バックエンド開発 >PHPチュートリアル >PHP はソートヒープソートアルゴリズムを実装します
PHP はソートヒープソートアルゴリズムを実装します
- jackloveオリジナル
- 2018-07-03 17:49:062912ブラウズ
この記事では、主に PHP で実装されたヒープ ソート アルゴリズムを詳しく紹介します。これには一定の参考価値があります。興味のある方は、
アルゴリズムの概要を参照してください:
ここで、「Dahua データ構造」の冒頭を直接引用します:
前に述べたように、単純な選択ソートでは、ソート対象の n 個のレコードの中から最小のレコードが選択されます。レコードは n - 1 回比較する必要があります。これは次のとおりです。最初のデータを見つけて何度も比較する必要があるのは普通のことですが、そうでない場合は、それが最小のレコードであることをどうやって知ることができますか。
残念ながら、この操作では各トリップの比較結果は保存されません。後のトリップの比較結果は重くなります。前のトリップでも多くの比較が行われましたが、前回のトリップの影響で、これらの比較結果は次のとおりです。並べ替え中に保存されないため、これらの比較操作は次の並べ替えパス中に繰り返され、より多くの比較が記録されました。
毎回最小のレコードを選択し、比較結果に基づいて他のレコードに対応する調整を行うことができれば、ソートの全体的な効率は非常に高くなります。ヒープ ソートは単純な選択ソートを改良したものであり、この改良の効果は非常に明白です。
基本的な考え方:
ヒープソートを紹介する前に、まずヒープについて紹介しましょう:
「Dahua データ構造」での定義: ヒープとは次のプロパティを持つ完全なバイナリ ツリー: 各ノードの値がその左右の子ノードの値以上で、大きなトップ ヒープ (大きなルート ヒープ) になる、または各ノードの値が以下またはその左右のノードの値と同じになり、小さなトップパイル (小さなルートパイル) になります。
これを見たときに私も「ヒープは完全なバイナリツリーなのか?」という疑問を持ちました。ネット上では完全なバイナリツリーではないという意見もありますが、 heap は完全なバイナリ ツリーですが、私はまだ意見を保留しています。ここでは、主に保存と計算を容易にするために、完全なバイナリ ツリーの形式で大きなルート ヒープ (小さなルート ヒープ) を使用していることだけを知っておく必要があります (利便性については後で説明します)。
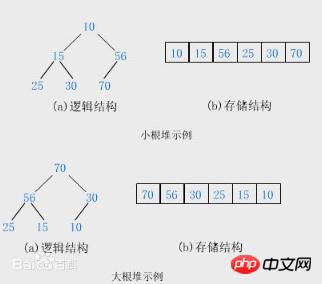
ヒープ ソート アルゴリズム:
ヒープ ソートは、ヒープ (大きなルート ヒープを想定) を使用してソートする方法です。基本的な考え方は、大きなルート ヒープにソートされるシーケンスを構築することです。このとき、シーケンス全体の最大値はヒープの先頭のルートノードとなる。それを削除し (実際には、それをヒープ配列の最後の要素と交換します。このとき、最後の要素が最大値になります)、残りの n - 1 シーケンスをヒープに再構築して、n 要素を取得します。次に小さい値。これを繰り返し実行すると、順序付けられたシーケンスが得られます。
大規模ルート ヒープ ソート アルゴリズムの基本操作:
①ヒープの構築. ヒープの構築は、len/2 から最初のノードに到達するまでヒープを継続的に調整するプロセスです。ここで、len はヒープ内の要素の数です。ヒープを構築するプロセスは線形プロセスです。ヒープを調整するプロセスは常に len/2 から 0 まで呼び出されます。これは o(h1) o(h2) ... o(hlen/2) に相当します。ここで hはノードの深さを表し、 len/2 はノードの数を表します。これは合計プロセスであり、結果は線形 O(n) です。
②調整ヒープ: 調整ヒープは、ヒープの構築プロセスで使用され、ヒープのソートプロセスでも使用されます。アイデアは、ノード i とその子ノード left(i) および right(i) を比較し、3 つのうちの最大 (または最小) を選択することです。最大 (最小) の値がノード i ではなく、その子ノードの 1 つである場合は、そこで、ノード i はノードと対話し、ヒープ調整プロセスを呼び出します。これは再帰的なプロセスです。ヒープ調整処理の時間計算量はヒープの深さに関係しており、深さ方向に調整するため lgn の演算となります。
③ヒープソート: ヒープソートは上記 2 つのプロセスを使用して実行されます。 1 つ目は、要素に基づいてヒープを構築することです。次に、ヒープのルート ノードを取り出し (通常は最後のノードと交換します)、最初の len-1 ノードでヒープ調整プロセスを続行し、すべてのノードが取り出されるまでルート ノードを取り出します。ヒープソートプロセスの時間計算量は O(nlgn) です。ヒープの構築の時間計算量は O(n) (1 回の呼び出し)、ヒープの調整の時間計算量は lgn で、n-1 回呼び出されるため、ヒープのソートの時間計算量は O(nlgn) です。
このプロセスを明確に理解するには多くの図が必要ですが、私は怠け者です。 。 。 。 。 。
アルゴリズム実装:
<?php
//堆排序(对简单选择排序的改进)
function swap(array &$arr,$a,$b){
$temp = $arr[$a];
$arr[$a] = $arr[$b];
$arr[$b] = $temp;
}
//调整 $arr[$start]的关键字,使$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意这里节点 s 的左右孩子是 2*s + 1 和 2*s+2 (数组开始下标为 0 时)
function HeapAdjust(array &$arr,$start,$end){
$temp = $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算(我这里数组开始下标识 0)
//左孩子2 * $start + 1,右孩子2 * $start + 2
for($j = 2 * $start + 1;$j <= $end;$j = 2 * $j + 1){
if($j != $end && $arr[$j] < $arr[$j + 1]){
$j ++; //转化为右孩子
}
if($temp >= $arr[$j]){
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start] = $arr[$j];
//继续往下
$start = $j;
}
$arr[$start] = $temp;
}
function HeapSort(array &$arr){
$count = count($arr);
//先将数组构造成大根堆(由于是完全二叉树,所以这里用floor($count/2)-1,下标小于或等于这数的节点都是有孩子的节点)
for($i = floor($count / 2) - 1;$i >= 0;$i --){
HeapAdjust($arr,$i,$count);
}
for($i = $count - 1;$i >= 0;$i --){
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新树($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i - 1);
}
}
$arr = array(9,1,5,8,3,7,4,6,2);
HeapSort($arr);
var_dump($arr);
時間計算量分析:
実行時間はわずかですは、最初のビルド ペアと再ビルド パイルの繰り返しのスクリーニングで消費されます。
一般に、ヒープ ソートの時間計算量は O(nlogn) です。ヒープ ソートは元のレコードのソート状態に影響されないため、最高、最低、平均の時間計算量は O(nlogn) です。これは、バブリング、単純な選択、直接挿入の O(n^2) 時間計算量よりも明らかにパフォーマンスがはるかに優れています。
ヒープソートは不安定なソート方法です。
このブログは「Dahua データ構造」から参照されています。将来の参考のためにここに記録されるだけです。批判しないでください。
興味があるかもしれない記事:
WeChat Tiaoyitiao PHP コード実装の詳細な説明
#PHP に実装されている WeChat の Moments への共有と共有数の記録機能の説明
#
以上がPHP はソートヒープソートアルゴリズムを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

