赤黒ツリーをJSで操作する方法

今回はJSで赤黒ツリーを操作する方法と、JSで赤黒ツリーを操作する際の注意点を紹介します。以下は実践的なケースですので見てみましょう。

赤黒木の性質

以下の性質を満たす二分探索木は赤黒木です

1. 各ノードは黒か赤のいずれかです。

2. ルートノードは黒です。

3. 各リーフノード (NIL) は黒です。

4. ノードが赤の場合、その子ノードは両方とも黒です。

5. 各ノードについて、そのノードからそのすべての子孫リーフ ノードへの単純なパスには、同じ数の黒いノードが含まれます。

プロパティ 1 とプロパティ 2 については、あまり説明する必要はありません。

プロパティ 3、各リーフ ノード (NIL) は黒です。ここでのリーフ ノードは、上図のノード 1、5、8、15 を指しますが、下図の null 値を持つノードを指します。その色は黒であり、親ノードの子ノードです。 。

プロパティ 4、ノードが赤の場合 (図では赤の代わりに白が使用されています)、その 2 つの子ノード (ノード 2、5、8、15 など) は黒になります。ただし、ノードの両方の子ノードが黒である場合、ノード 1 のように、そのノードは赤ではない可能性があります。

プロパティ 5、各ノードについて、そのノードからそのすべての子孫リーフ ノードへの単純なパスには、同じ数の黒いノードが含まれます。たとえば、ノード 2 からそのすべての子孫リーフ ノードへの単純なパスでは、黒いノードの数は 2 です。ルート ノード 11 からそのすべての子孫のリーフ ノードへの単純なパスでは、黒いノードの数は 2 です。 。

そのような木の特徴は何ですか？

ルートからリーフノードまでの単純なパス上の各ノードの色を制限することにより、赤黒ツリーは、ほぼバランスが取れているため、どのパスも他のパスの 2 倍の長さになることがなくなります。 ——「アルゴリズム入門」

性質 4 により、赤黒ツリーでは 2 つの赤いノードは隣接しません。ツリー内で可能な最短のパスはすべて黒色のノードを持つパスであり、ツリー内で可能な最長のパスは赤色のノードと黒色のノードが交互にあるパスです。プロパティ 5 と組み合わせると、各パスには同じ数の黒いノードが含まれるため、赤黒ツリーによって、どのパスも他のパスの 2 倍の長さになることがなくなります。

赤黒ツリーの挿入

まず二分探索木にノードを挿入し、赤色に着色します。黒の場合は特性 5 に違反するため調整が不便ですが、赤の場合は特性 2 または特性 4 に違反する可能性があります。比較的簡単な操作で赤黒の木の特性に戻すことができます。

二分探索木にノードが挿入された後、次の状況が発生する可能性があります:

ケース 1

ノードが挿入された後、親ノードがなく、ノードがルート ノードになるように挿入されます。プロパティ 2 に違反している場合は、ノードを黒に調整して挿入を完了します。

ケース 2

ノードを挿入した後、その親ノードは黒になり、どのプロパティにも違反しません。調整は必要なく、挿入は完了します。たとえば、次の図にノード 13 を挿入します。

ケース 3

ノードを挿入した後、その親ノードは赤になります。これはプロパティ 4 に違反しており、一連の調整が必要です。たとえば、次の図にノード 4 を挿入します。

では、一連の調整とは何でしょうか？

挿入されたノードノードの親ノードの父が赤の場合、ノードの父には黒の親ノードの祖父が必要です。なぜなら、ノードの父に親ノードがない場合、それがルートノードであり、ルートノードが黒です。この場合、ノード祖父の他の子ノードは、ノードおじさんと呼ばれることができ、これはノード父の兄弟ノードである。ノードおじさんは黒または赤の場合があります。

最初に最も単純な状況を分析しましょう。複雑な状況は単純な状況に変換できます。単純な状況とは、ノードのおじさんが黒人の状況です。

シナリオ3.1

上記(a)に示すように、状況は次のようになります。ノードが赤、父親が赤、祖父と叔父が黒、α、β、θ、ω、ηはすべて子です。ノードツリー。二分探索木全体のうち、性質 4 に違反して、ノードと父親だけが正常な赤黒木になれなかったとします。このとき、画像 (a) を画像 (b) に調整すると、正常な赤黒木に戻すことができます。黒い木。調整プロセス全体は、実際には回転と色の変更の 2 つのステップに分かれています。

ローテーションとは何ですか?

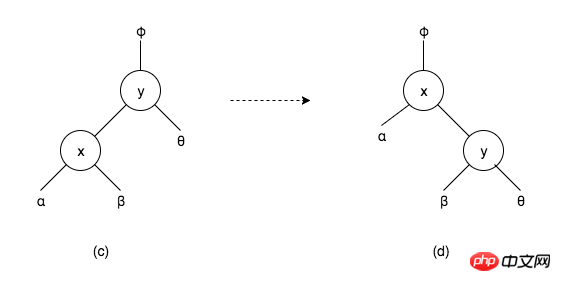
上の図 (c) に示すように、これは二分探索木の一部であり、x、y はノード、α、β、θ は対応するノードのサブツリーです。図から、α

ノードは赤、父は赤、祖父と叔父は黒です。具体的な状況 1

図 (a) では、ノードは父の左の子ノード、父はグランドの左の子ノード、ノード ; θ

色の変更

ということで、写真(a)を回転させた後、グランドを赤に、ファーザーを黒に変更して、写真(b)になり挿入完了です。

ノードが赤、父が​​赤、祖父と叔父が黒

ノードが父の右子ノード、父がグランドの右子ノードです。 、具体的なケースのフリップです。

つまり、叔父<グランド<父親<ノードを図(e)で回転させ、色を変更して図(f)に変更します。図 (m) に示すように、

ノードが赤、父が​​赤、祖父と叔父が黒の具体的なケース 3 は、

ノードが父の右の子ノード、父がグランドの左の子ノードです。下に。

図(m)のノードと父親を回転させると、図(n)になり、父親を新しいノードとして扱い、特定の状況1になります。再度回転し、色を変更して、挿入を完了します。

ノードは赤、父は赤、祖父と叔父は黒、具体的なケース4。以下の図(i)に示すように、

ノードは父の右の子ノード、父はグランドの左の子ノードです。は特殊なケースです。 3. 反転します。

図(i)のノードと父親を回転させると、図(j)になり、父親を新しいノードとして扱い、特定の状況になります。 2. 再度回転し、色を変更して、挿入が完了します。

ケース 3.2

ノード、父と叔父は赤、祖父は黒です。

上の写真(k)のように、回転するのではなく、グランドを赤、父と叔父を黒に着色し、グランドを新たなノードとして状況を判断します。グランドが新しいノードになるとケース 2 になり、調整後ケース 3.1 になると挿入が完了します。引き続きケース 3.2 になると、グランド、父親、叔父の色を変更し続けます。 , and ノード 新しいノードに親ノードがない場合は、ケース 1 になります。ルート ノードが黒く表示され、挿入が完了します。

要約すると

	ノードの状況	操作
ケース1	ノードは赤で、父親はありません	ノードの色を変更
ケース2	ノードは赤、父は黒です
ケース3.1	ノード、父は赤、祖父、叔父は黒	1回または2回回転して色を変更します
ケース3.2	ノード、父、叔父は赤、祖父は黒です	父、おじさん、グランド、グランドを新しいノードとして

コード

// 结点
function Node(value) {
 this.value = value
 this.color = 'red' // 结点的颜色默认为红色
 this.parent = null
 this.left = null
 this.right = null
}
function RedBlackTree() {
 this.root = null
}
RedBlackTree.prototype.insert = function (node) {
 // 以二叉搜索树的方式插入结点
 // 如果根结点不存在，则结点作为根结点
 // 如果结点的值小于node，且结点的右子结点不存在，跳出循环
 // 如果结点的值大于等于node，且结点的左子结点不存在，跳出循环
 if (!this.root) {
 this.root = node
 } else {
 let current = this.root
 while (current[node.value <= current.value ? 'left' : 'right']) {
  current = current[node.value <= current.value ? 'left' : 'right']
 }
 current[node.value <= current.value ? 'left' : 'right'] = node
 node.parent = current
 }
 // 判断情形
 this._fixTree(node)
 return this
}
RedBlackTree.prototype._fixTree = function (node) {
 // 当node.parent不存在时，即为情形1，跳出循环
 // 当node.parent.color === 'black'时，即为情形2，跳出循环
 while (node.parent && node.parent.color !== 'black') {
 // 情形3
 let father = node.parent
 let grand = father.parent
 let uncle = grand[grand.left === father ? 'right' : 'left']
 if (!uncle || uncle.color === 'black') {
  // 叶结点也是黑色的
  // 情形3.1
  let directionFromFatherToNode = father.left === node ? 'left' : 'right'
  let directionFromGrandToFather = grand.left === father ? 'left' : 'right'
  if (directionFromFatherToNode === directionFromGrandToFather) {
  // 具体情形一或二
  // 旋转
  this._rotate(father)
  // 变色
  father.color = 'black'
  grand.color = 'red'
  } else {
  // 具体情形三或四
  // 旋转
  this._rotate(node)
  this._rotate(node)
  // 变色
  node.color = 'black'
  grand.color = 'red'
  }
  break // 完成插入，跳出循环
 } else {
  // 情形3.2
  // 变色
  grand.color = 'red'
  father.color = 'black'
  uncle.color = 'black'
  // 将grand设为新的node
  node = grand
 }
 }
 if (!node.parent) {
 // 如果是情形1
 node.color = 'black'
 this.root = node
 }
}
RedBlackTree.prototype._rotate = function (node) {
 // 旋转 node 和 node.parent
 let y = node.parent
 if (y.right === node) {
 if (y.parent) {
  y.parent[y.parent.left === y ? 'left' : 'right'] = node
 }
 node.parent = y.parent
 if (node.left) {
  node.left.parent = y
 }
 y.right = node.left
 node.left = y
 y.parent = node
 } else {
 if (y.parent) {
  y.parent[y.parent.left === y ? 'left' : 'right'] = node
 }
 node.parent = y.parent
 if (node.right) {
  node.right.parent = y
 }
 y.left = node.right
 node.right = y
 y.parent = node
 }
}
let arr = [11, 2, 14, 1, 7, 15, 5, 8, 4, 16]
let tree = new RedBlackTree()
arr.forEach(i => tree.insert(new Node(i)))
debugger

 この記事のケースを読んだ後は、この方法を習得したと思います。さらに興味深い情報については、PHP 中国語 Web サイトの他の関連記事に注目してください。 
推奨読書: 
jQueryは、入力テキストが指定された行数を超えた場合に省略記号の自動追加を実装します
関連する要素パラメータを取得するためのJSのEL式
Vueのカスタム動的コンポーネントの使用状況分析
以上が赤黒ツリーをJSで操作する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。