Python は最大公約数を解くメソッドを実装します

今回は、最大公約数を解決するための Python メソッドを紹介します。 最大公約数を解決するための Python の メモ は何ですか? ここでは実際のケースを見てみましょう。

まずアルゴリズムの説明をインターネットから抜粋すると以下の通りです:

追加位相減算法:更新位相減算法とも呼ばれ、「算術九章」より最大公約数を求めるアルゴリズムです。本来はリダクション用に設計されたものですが、最大公約数が求められるあらゆる場面に適しています。

「算術九章」は、古代中国の数学の論文で、その中にある「追加の減算法」は、2 つの数値の最大公約数を求めるために使用できます。つまり、「半分が半分にできる場合は、半分になります。」それは半分であり、半分が半分になれない場合はその逆です。」 分母と引き算の数を設定し、引き算の数を減らすことで引き算の数を減らします。ステップ 1: 任意の 2 つの正の整数 が与えられ、それらがすべて偶数であるかどうかを判断します。はいの場合は 2 を使用して削減し、そうでない場合は 2 番目のステップを実行します。

ステップ 2: 大きい数値から小さい数値を引き、得られた差を小さい数値と比較し、大きい数値から数値を減らします。結果の減数と差が等しくなるまでこの操作を続けます。

上記の説明を読んだ後の私の最初の反応は、この説明に何か問題があるのではないかということでした。普遍性という点では問題もあるはずだ。たとえば、4 と 4 の最大公約数を見つけた場合、半分と半分の後の結果は間違っているはずです。次のアルゴリズムも実行できません。 とにかく、最初に上記のアルゴリズムの説明を実装しましょう:

# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
  # even process
  while m % 2 == 0 and n % 2 == 0:
    m = m / 2
    n = n / 2
  # exchange order when needed
  if m < n:
    m,n = n,m
  # calculate the max comm pisor
  while m - n != n:
    diff = m - n
    if diff > n:
      m = diff
    else:
      m = n
      n = diff
  return n
print(MaxCommpisor(55,120))
print(MaxCommpisor(55,77))
print(MaxCommpisor(32,64))
print(MaxCommpisor(16,128))

動作結果:

言うまでもなく、上記のプログラムの実行はエラーでいっぱいです。それで、それを修正するにはどうすればよいでしょうか？

まず、2で割ったものはすべて最後に逆算する必要があります。このようにして、プログラムは次のように変更されます。

def MaxCommpisor(m,n):
  com_factor = 1
  if m == n:
    return n
  else:
    # process for even number
    while m % 2 == 0 and n % 2 == 0:
      m = int(m / 2)
      n = int(n / 2)
      com_factor *= 2
    if m < n:
      m,n = n,m
    diff = m - n
    while n != diff:
      m = diff
      if m < n:
        m,n = n,m
      diff = m - n
    return n * com_factor
print(MaxCommpisor(55,120))
print(MaxCommpisor(55,77))
print(MaxCommpisor(32,64))
print(MaxCommpisor(16,128))

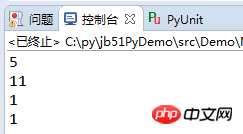変更後の上記プログラムの実行結果は次のとおりです

このプログラムを作成すると、少し奇妙に見えますが、全体的なアルゴリズムは依然として実装されています。ユークリッド除算などのアルゴリズムと比較すると、

ループ

のレベルでこの確率はある程度軽減されます。特に、テスト番号の最後の 2 つのペアについては、この場合の効果がより優れています。ただし、アルゴリズムの全体的な効率を正確に測定することはまだできません。

この記事の事例を読んだ後、あなたはその方法をマスターしたと思います。さらに興味深い情報については、php 中国語 Web サイトの他の関連記事に注目してください。

推奨読書:

Pycharm の使用スキルのまとめ

Python で 2 次元配列のローカル ピーク値を取得する方法

以上がPython は最大公約数を解くメソッドを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。