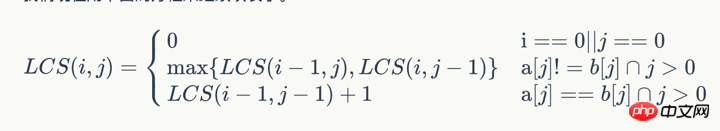0 |
|
そして、2 つの文字列間で比較される文字が異なる場合、塗りつぶされるグリッドは左辺または上辺に関連しており、大きい方の辺が使用されることがわかります。
比較される文字が同じ場合でも、心配する必要はありません。X の C は Y の C、つまり ABC {"",A,B,C, の部分シーケンス セットと比較する必要があることが起こります。 AB,BC,ABC} および BDC 部分列セット {"",B,D,C,BD,DC,BDC} を比較すると、得られる共通部分文字列は "",B,D です。この時点でも結論は前と同じで、文字が等しい場合、対応するグリッドの値は左隅、右隅、左上隅の値に等しく、左辺、上辺、左上辺は次のようになります。常に平等です。これらの謎を証明するには、より厳密な数学的知識が必要です。
A と B という 2 つの配列があるとします。 A[i] は A の i 番目の要素、A(i) は A の最初の要素から i 番目の要素で構成される接頭辞です。 m(i, j) は、A(i) と B(j) の最長の共通部分列長です。
アルゴリズム自体の再帰的な性質により、実際には、特定の i と j について次のことを証明するだけで済みます:
m(i, j) = m(i-1, j-1) + 1 ( A[i] = B [j]の場合)
m(i, j) = max( m(i-1, j), m(i, j-1) ) (A[i] != B[の場合) j])
最初の式、つまり A[i] = B[j] の場合は証明するのが簡単です。 m(i, j) > m(i-1, j-1) + 1 (m(i, j) が m(i-1, j-1) + 未満であると仮定すると、反証を使用できます。 1 には十分な理由があります (明らかに)、m(i-1, j-1) が最長ではないという矛盾した結果が推測できます。
2つ目は少し難しいです。 A[i] != B[j] の場合でも、m(i, j) > max( m(i-1, j), m(i, j-1) ) と仮定すると、これは反証です。
反証仮説により、m(i, j) > m(i-1, j) が得られます。これは、A[i] が m(i, j) に対応する LCS シーケンス内に存在する必要があると推測できます (矛盾する証拠が利用可能です)。また、A[i] != B[j] であるため、B[j] は m(i, j) に対応する LCS シーケンス内にあってはなりません。したがって、m(i, j) = m(i, j-1) と推定できます。いずれにしても仮説に反する結果が得られます。
認定を取得しましょう。
ここで、以下の方程式を使用して表への入力を続けます。
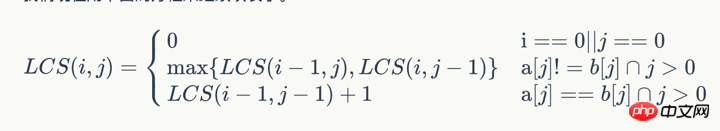
プログラムの実装
//by 司徒正美
function LCS(str1, str2){
var rows = str1.split("")
rows.unshift("")
var cols = str2.split("")
cols.unshift("")
var m = rows.length
var n = cols.length
var dp = []
for(var i = 0; i < m; i++){
dp[i] = []
for(var j = 0; j < n; j++){
if(i === 0 || j === 0){
dp[i][j] = 0
continue
}
if(rows[i] === cols[j]){
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
}else{
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1]) //对左边,上边取最大
}
}
console.log(dp[i].join(""))//调试
}
return dp[i-1][j-1]
}LCSは、位置を移動するだけでさらに簡素化でき、新しい配列を生成する必要がなくなります
//by司徒正美
function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)] //第一行全是0
for(var i = 1; i <= m; i++){ //一共有m+1行
dp[i] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
} else {
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1])
}
}
}
return dp[m][n];
}LCSの印刷
印刷機能を与えますので、やってみましょうまず、印刷する方法を見てください。右下隅から見て一番上の行で終わります。したがって、ターゲット文字列は逆の順序で構築されます。 stringBuffer などの面倒な中間量の使用を避けるために、プログラムが実行されるたびに 1 つの文字列のみが返され、それ以外の場合は printLCS(x,y,...) + を使用して空の文字列が返されます。 str[ i] は、必要な文字列を取得するために追加されます。
取得した文字列が実際の LCS 文字列であるかどうかを確認する別のメソッドを作成しましょう。すでに働いている人間として、単体テストを行って他の人が実行できるようにオンラインに公開しない限り、学校の学生のようにコードを書くことはできません。
//by 司徒正美,打印一个LCS
function printLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return "";
}
if( str1[i-1] == str2[j-1] ){
return printLCS(dp, str1, str2, i-1, j-1) + str1[i-1];
}else{
if (dp[i][j-1] > dp[i-1][j]){
return printLCS(dp, str1, str2, i, j-1);
}else{
return printLCS(dp, str1, str2, i-1, j);
}
}
}
//by司徒正美, 将目标字符串转换成正则,验证是否为之前两个字符串的LCS
function validateLCS(el, str1, str2){
var re = new RegExp( el.split("").join(".*") )
console.log(el, re.test(str1),re.test(str2))
return re.test(str1) && re.test(str2)
}
使用:
function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printLCS(dp, str1, str2, m, n)
validateLCS(s, str1, str2)
return dp[m][n]
}
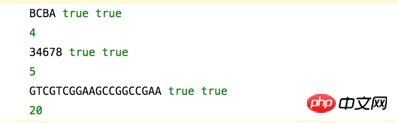
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA
Print all LCS
この考え方は、LCS メソッドに Math.max 値があることに注意してください。これは、実際には 3 つの状況を統合します。したがって、3本の弦をフォークすることができます。このメソッドは、自動削除のために es6 コレクション オブジェクトを返します。その後、毎回新しいセットを使用して古いセットの文字列がマージされます。
//by 司徒正美 打印所有LCS
function printAllLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return new Set([""])
}else if(str1[i-1] == str2[j-1]){
var newSet = new Set()
printAllLCS(dp, str1, str2, i-1, j-1).forEach(function(el){
newSet.add(el + str1[i-1])
})
return newSet
}else{
var set = new Set()
if (dp[i][j-1] >= dp[i-1][j]){
printAllLCS(dp, str1, str2, i, j-1).forEach(function(el){
set.add(el)
})
}
if (dp[i-1][j] >= dp[i][j-1]){//必须用>=,不能简单一个else搞定
printAllLCS(dp, str1, str2, i-1, j).forEach(function(el){
set.add(el)
})
}
return set
}
}
使用:
function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printAllLCS(dp, str1, str2, m, n)
console.log(s)
s.forEach(function(el){
validateLCS(el,str1, str2)
console.log("输出LCS",el)
})
return dp[m][n]
}
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA

空間最適化
ローリング配列を使用:
function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)],now = 1,row //第一行全是0
for(var i = 1; i <= m; i++){ //一共有2行
row = dp[now] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[now][j] = dp[i-now][j-1] + 1 //对角+1
} else {
dp[now][j] = Math.max( dp[i-now][j], dp[now][j-1])
}
}
now = 1- now; //1-1=>0;1-0=>1; 1-1=>0 ...
}
return row ? row[n]: 0
}
危険な再帰的解決策
str1のサブシーケンスは添字シーケンス {1, 2 , ... に対応します。 .., m} の部分列 したがって、str1 には合計 ${2^m}$ 個の異なる部分列があり (${2^n}$ などの str2 にも同じことが当てはまります)、その複雑さは驚くべきものに達します。指数時間 (${2^m * 2^n}$)。
//警告,字符串的长度一大就会爆栈
function LCS(str1, str2, a, b) {
if(a === void 0){
a = str1.length - 1
}
if(b === void 0){
b = str2.length - 1
}
if(a == -1 || b == -1){
return 0
}
if(str1[a] == str2[b]) {
return LCS(str1, str2, a-1, b-1)+1;
}
if(str1[a] != str2[b]) {
var x = LCS(str1, str2, a, b-1)
var y = LCS(str1, str2, a-1, b)
return x >= y ? x : y
}
}
この記事の事例を読んだ後は、この方法を習得したと思います。さらに興味深い情報については、php 中国語 Web サイトの他の関連記事に注目してください。
推奨読書:
datepicker の使用方法
NavigatorIOSコンポーネントの使い方の詳しい説明
Vue.jsでのejsExcelテンプレートの使い方