ホームページ >ウェブフロントエンド >CSSチュートリアル >JavaScriptトライプレフィックスツリーの使い方を詳しく解説
JavaScriptトライプレフィックスツリーの使い方を詳しく解説
- php中世界最好的语言オリジナル
- 2018-03-23 09:47:031629ブラウズ
今回は javascript trie プレフィックス ツリーの使用方法について詳しく説明します。 javascript trie プレフィックス ツリーを使用する際の 注意事項 について、以下に具体的な事例を示します。
はじめに
トライ ツリー (単語検索に由来) は、プレフィックス ワード、単語検索ツリー、辞書ツリーとも呼ばれ、ツリー構造、ハッシュ ツリーの変形、およびマルチツリー構造です。素早い検索。 その利点は、不必要な文字列比較 を最小限に抑え、クエリ効率がハッシュ テーブルよりも高いことです。
Trie の核となるアイデアは、空間を時間と交換することです。文字列の共通プレフィックスを使用してクエリ時間のオーバーヘッドを削減し、効率を向上させます。 Trie ツリーにも欠点があります。文字と数字のみを処理すると仮定すると、各ノードには少なくとも 52+10 の子ノードがあります。メモリを節約するには、リンクされたリストまたは配列を使用できます。 JS 配列は動的であり、最適化が組み込まれているため、JS では配列を直接使用します。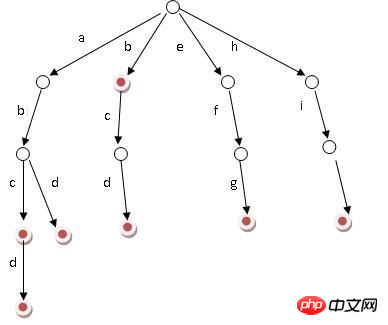
基本プロパティ
- ルートノードには文字が含まれず、ルートノードを除くすべての子ノードには文字が1つ含まれます
- ルートノードから特定のノードまで。パス上を通過する文字は接続されており、これはノードに対応する文字列です。Trie の挿入メソッドでは、各ノードのすべてのサブノードに異なる文字が含まれます。 辞書ツリーは主に単語頻度統計に使用されるため、numPass、numEnd を含む多くのノード属性がありますが、非常に重要な属性です。 insert メソッドは、重い単語を挿入するために使用されます。開始する前に、その単語が正当な文字であり、空白を使用できないかどうかを判断する必要があります。挿入時、文字は分割されて各ノードに配置されます。 numPass は、ノードが渡されるたびに変更する必要があります。
最適化
// by 司徒正美
class Trie {
constructor() {
this.root = new TrieNode();
}
isValid(str) {
return /^[a-z1-9]+$/i.test(str);
}
insert(word) {
// addWord
if (this.isValid(word)) {
var cur = this.root;
for (var i = 0; i < word.length; i++) {
var c = word.charCodeAt(i);
c -= 48; //减少”0“的charCode
var node = cur.son[c];
if (node == null) {
var node = (cur.son[c] = new TrieNode());
node.value = word.charAt(i);
node.numPass = 1; //有N个字符串经过它
} else {
node.numPass++;
}
cur = node;
}
cur.isEnd = true; //樯记有字符串到此节点已经结束
cur.numEnd++; //这个字符串重复次数
return true;
} else {
return false;
}
}
remove(word){
if (this.isValid(word)) {
var cur = this.root;
var array = [], n = word.length
for (var i = 0; i < n; i++) {
var c = word.charCodeAt(i);
c = this.getIndex(c)
var node = cur.son[c];
if(node){
array.push(node)
cur = node
}else{
return false
}
}
if(array.length === n){
array.forEach(function(){
el.numPass--
})
cur.numEnd --
if( cur.numEnd == 0){
cur.isEnd = false
}
}
}else{
return false
}
}
preTraversal(cb){//先序遍历
function preTraversalImpl(root, str, cb){
cb(root, str);
for(let i = 0,n = root.son.length; i < n; i ++){
let node = root.son[i];
if(node){
preTraversalImpl(node, str + node.value, cb);
}
}
}
preTraversalImpl(this.root, "", cb);
}
// 在字典树中查找是否存在某字符串为前缀开头的字符串(包括前缀字符串本身)
isContainPrefix(word) {
if (this.isValid(word)) {
var cur = this.root;
for (var i = 0; i < word.length; i++) {
var c = word.charCodeAt(i);
c -= 48; //减少”0“的charCode
if (cur.son[c]) {
cur = cur.son[c];
} else {
return false;
}
}
return true;
} else {
return false;
}
}
isContainWord(str) {
// 在字典树中查找是否存在某字符串(不为前缀)
if (this.isValid(word)) {
var cur = this.root;
for (var i = 0; i < word.length; i++) {
var c = word.charCodeAt(i);
c -= 48; //减少”0“的charCode
if (cur.son[c]) {
cur = cur.son[c];
} else {
return false;
}
}
return cur.isEnd;
} else {
return false;
}
}
countPrefix(word) {
// 统计以指定字符串为前缀的字符串数量
if (this.isValid(word)) {
var cur = this.root;
for (var i = 0; i < word.length; i++) {
var c = word.charCodeAt(i);
c -= 48; //减少”0“的charCode
if (cur.son[c]) {
cur = cur.son[c];
} else {
return 0;
}
}
return cur.numPass;
} else {
return 0;
}
}
countWord(word) {
// 统计某字符串出现的次数方法
if (this.isValid(word)) {
var cur = this.root;
for (var i = 0; i < word.length; i++) {
var c = word.charCodeAt(i);
c -= 48; //减少”0“的charCode
if (cur.son[c]) {
cur = cur.son[c];
} else {
return 0;
}
}
return cur.numEnd;
} else {
return 0;
}
}
}
class TrieNode {
constructor() {
this.numPass = 0;//有多少个单词经过这节点
this.numEnd = 0; //有多少个单词就此结束
this.son = [];
this.value = ""; //value为单个字符
this.isEnd = false;
}
} 。次に、関連するメソッドは、 c-= 48 を c = this.getIndex(c) に変更することですTest// by 司徒正美
getIndex(c){
if(c < 58){//48-57
return c - 48
}else if(c < 91){//65-90
return c - 65 + 11
}else {//> 97
return c - 97 + 26+ 11
}
}
トライ木と他のデータ構造の比較
トライ木とバイナリ検索ツリー二分探索ツリーは、私たちが最初に接触するツリー構造であるはずです。データサイズがnのとき、二分探索ツリーの挿入、検索、および削除操作の時間計算量は通常わずかO(log)であることがわかっています。 n ) の場合、最悪の場合、ツリー全体のすべてのノードが 1 つの子ノードのみを持ち、線形リストに縮退します。このとき、挿入、検索、および削除の操作の時間計算量は O(n) になります。 通常、トライ木の高さ n は検索文字列の長さ m よりもはるかに大きいため、検索操作の時間計算量は通常 O(m) であり、最悪の場合の時間計算量は O(n )。トライ ツリーでの最悪の場合の検索が二分探索ツリーよりも高速であることが簡単にわかります。
この記事のトライ ツリーは例として文字列を使用しています。実際、キーが浮動小数点数の場合、トライ ツリー全体が非常に長くなり、ノードが長くなる可能性があります。可読性が低いため、この場合、データを保存するためにトライ ツリーを使用するのは適切ではありません。二分探索ツリーではこの問題は発生しません。 
トライツリーとハッシュテーブル ハッシュの競合の問題について考えてみましょう。通常、ハッシュ テーブルの複雑さは O(1) であると言われますが、実際、これは完全に近いハッシュ テーブルの複雑さです。さらに、ハッシュ関数自体が必要とすることも考慮する必要があります。検索文字列を走査するための計算量は O(m ) です。異なるキーが「同じ位置」にマッピングされている場合 (クローズド ハッシュを考慮すると、この「同じ位置」は通常のリンク リストで置き換えることができます)、検索の複雑さは「同じ位置」番号の下のノードの数に依存します。したがって、最悪の場合、ハッシュ テーブルが一方向のリンク リストになる可能性もあります。 トライ ツリーは、キーのアルファベット順に従って簡単にソートできます (ツリー全体が順番に一度走査されます)。これは、ほとんどのハッシュ テーブルとは異なります (通常、ハッシュ テーブルには異なるキーのシーケンスに対する機能がありません)。 理想的な状況では、ハッシュ テーブルは O(1) の速度でターゲットに迅速にヒットします。テーブルが非常に大きく、ディスク上に配置する必要がある場合、ハッシュ テーブルの検索アクセスは 1 回だけ行う必要があります。理想的な状況ではありますが、トライ ツリーによってアクセスされるディスクの数はノードの深さと同じである必要があります。 多くの場合、トライ ツリーはハッシュ テーブルよりも多くのスペースを必要とします。1 つのノードが 1 つの文字を保存する状況を考慮すると、文字列を保存するときにそれを別のブロックとして保存する方法はありません。トライ ツリーのノード圧縮により、この問題を大幅に軽減できます。これについては後で説明します。 トライ木の改良 Bitwise Trie(ビットワイズトライ) 通常のトライ木に格納される最小単位が文字である点を除けば原理的には通常のトライ木と同様ですが、 Bitwise Try はビットのみを保存します。ビットデータのアクセスは、CPU 命令によって 1 回直接実装されます。バイナリデータの場合、理論的には通常のトライ木よりも高速です。 ノード圧縮。 ブランチ圧縮: 安定したトライツリー、基本的に検索および読み取り操作の場合、一部のブランチを圧縮できます。たとえば、前の図の右端のブランチの inn は、通常のサブツリーとして存在せずに、ノード「inn」に直接圧縮できます。基数ツリーは、トライ ツリーが深すぎるという問題を解決するために、この原理に基づいています。 ノード マッピング テーブル: この方法は、トライ ツリー内のノードの各状態がほぼ完全に決定されている場合、状態の合計数が によって繰り返される場合にも使用されます。要素は数値です。多次元配列 (Triple Array Trie など) が表現されるため、追加のマッピング テーブルが導入されますが、Trie ツリー自体を格納するスペースのオーバーヘッドは小さくなります。 プレフィックスツリーの応用 プレフィックスツリーはやはり理解しやすく、その応用範囲も非常に広いです。 (1) 文字列の高速検索 辞書ツリーのクエリ時間計算量はO(logL)、Lは文字列の長さです。したがって、効率は依然として比較的高いです。ディクショナリ ツリーはハッシュ テーブルよりも効率的です。 (2) 文字列の並べ替え 上の図から、単語が並べ替えられ、最初にアルファベット順にたどられていることが簡単にわかります。不要な共通部分文字列を減らします。 (3) 最長の共通接頭辞 inn と int の最長の共通接頭辞は in です。辞書ツリーを文字 n までたどると、この時点でこれらの単語の共通接頭辞は in になります。 (4) 接頭辞を自動的に照合して接尾辞を表示します 辞書や検索エンジンを使用する場合、「appl」と入力すると、接頭辞が「appl」のものが自動的に表示されます。前述したように、辞書ツリーは残りの接尾辞をたどって表示するだけで済みます。 以上がこの記事の全内容です。皆様の学習に役立つことを願っています。また、皆様も Script House をサポートしていただければ幸いです。 この記事の事例を読んだ後は、この方法を習得したと思います。さらに興味深い情報については、php 中国語 Web サイトの他の関連記事に注目してください。 推奨読書:
以上がJavaScriptトライプレフィックスツリーの使い方を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

