PHP ヒープが TopK アルゴリズムを実装する例

バイナリ ヒープは特殊な種類のヒープです。バイナリ ヒープは、完全なバイナリ ツリー、またはほぼ完全なバイナリ ツリーです。最大ヒープと最小ヒープの 2 種類があります。親ノードのキー値は次のとおりです。常に子ノードのキー値以上です。 min-heap: 親ノードのキー値は常に​​子ノードのキー値以下です。

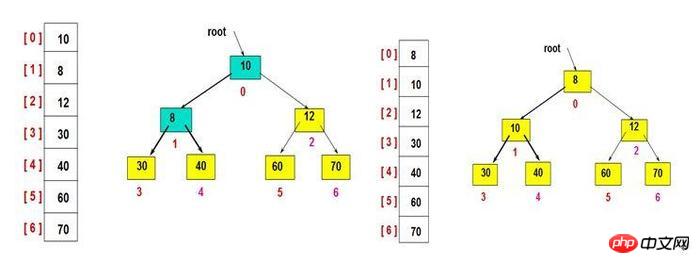
スモールトップヒープ - (インターネットからの画像)

---

バイナリヒープは通常、配列で表されます (上の図を参照)。たとえば、配列内のルート ノードの位置は 0 です。 n 番目の位置の子 ノードはそれぞれ 2n+1 と 2n+2 にあります。したがって、0 番目の位置の子ノードは 1 と 2 にあり、1 の子ノードは 3 と 4 にあります。 storage メソッドを使用すると、親ノードと子ノードを簡単に見つけることができます。

ここでは、具体的な概念的問題については詳しく説明しません。バイナリ ヒープについて質問がある場合は、このデータ構造をよく理解してください。次に、PHP コードを使用して上記を実装し、解決します。 topN の問題 違いを確認するには、まず並べ替えメソッドを使用して実装し、それがどのように機能するかを確認します。

クイックソートアルゴリズムを使用してTopNを実装します

//为了测试运行内存调大一点ini_set('memory_limit', '2024M');//实现一个快速排序函数function quick_sort(array $array){
    $length = count($array);    $left_array = array();    $right_array = array();    if($length <= 1){        return $array;
    }    $key = $array[0];    for($i=1;$i<$length;$i++){        if($array[$i] > $key){            $right_array[] = $array[$i];
        }else{            $left_array[] = $array[$i];
        }
    }    $left_array = quick_sort($left_array);    $right_array = quick_sort($right_array);    return array_merge($right_array,array($key),$left_array);    
}//构造500w不重复数for($i=0;$i<5000000;$i++){    $numArr[] = $i; 
}//打乱它们shuffle($numArr);//现在我们从里面找到top10最大的数var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());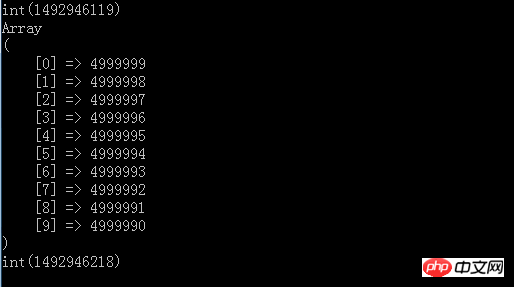

実行後の結果

---

上にトップ10の結果が出力され、実行時間が約99秒であることがわかりますが、これはすべての数値をメモリにロードできる場合、5kw または 5 億個の数値を含むファイルがある場合、間違いなくいくつかの問題が発生します

TopN を実装するにはバイナリ ヒープ アルゴリズムを使用します
実装プロセス。
1、最初に 10 または 100 個の数値を配列に読み取ります。これが topN 数値です。
2. この時点で、この配列から小さいトップ ヒープ構造を生成する関数を呼び出します。ヒープは最小である必要があります。
3. ファイルまたは配列の残りのすべての数値を順に走査します。
数値が走査されるたびに、そのサイズがヒープの先頭の要素と比較されます。ヒープの先頭の要素より大きい場合は、それを置き換えます
5 、ヒープの先頭の要素を置き換えた後、小さな先頭ヒープの生成関数を呼び出して続行します。最小のトップヒープを見つける必要があるため、スモールトップヒープを生成します。
6. すべての走査が完了すると、スモールトップヒープの中にあるものが最大のtopNになります。小さなトップ ヒープは常に最小のものを除外し、最大のものを残します。この小さなトップ ヒープの調整も、ルート ノードが左右のノードより小さい限り、非常に高速です。
7. アルゴリズムの複雑さの点では、最悪の場合、数値を毎回走査してヒープの先頭に置き換える場合、10 回調整する必要があり、これはソート速度よりも高速です。がすべてではありません。すべての内容がメモリに読み込まれます。実績は直線的な走査であることがわかります。

//生成小顶堆函数function Heap(&$arr,$idx){
    $left  = ($idx << 1) + 1;    $right = ($idx << 1) + 2;    if (!$arr[$left]){        return;
    }    if($arr[$right] && $arr[$right] < $arr[$left]){        $l = $right;
    }else{        $l = $left;
    }    if ($arr[$idx] > $arr[$l]){         $tmp = $arr[$idx]; 
         $arr[$idx] = $arr[$l];         $arr[$l] = $tmp;
         Heap($arr,$l);
    }
}//这里为了保证跟上面一致，也构造500w不重复数/*
  当然这个数据集并不一定全放在内存，也可以在
  文件里面，因为我们并不是全部加载到内存去进
  行排序
*/for($i=0;$i<5000000;$i++){    $numArr[] = $i;    
}//打乱它们shuffle($numArr);//先取出10个到数组$topArr = array_slice($numArr,0,10);//获取最后一个有子节点的索引位置//因为在构造小顶堆的时候是从最后一个有左或右节点的位置//开始从下往上不断的进行移动构造（具体可看上面的图去理解）$idx = floor(count($topArr) / 2) - 1;//生成小顶堆for($i=$idx;$i>=0;$i--){
    Heap($topArr,$i);
}

var_dump(time());//这里可以看到，就是开始遍历剩下的所有元素for($i = count($topArr); $i < count($numArr); $i++){    //每遍历一个则跟堆顶元素进行比较大小
    if ($numArr[$i] > $topArr[0]){        //如果大于堆顶元素则替换
        $topArr[0] = $numArr[$i];        /*
          重新调用生成小顶堆函数进行维护，只不过这次是从堆顶
          的索引位置开始自上往下进行维护，因为我们只是把堆顶
          的元素给替换掉了而其余的还是按照根节点小于左右节点
          的顺序摆放这也就是我们上面说的，只是相对调整下，并
          不是全部调整一遍
        */
        Heap($topArr,0);
    }
}
var_dump(time());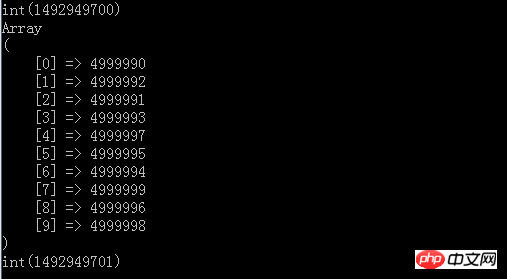

最終結果もtop10であることがわかります。時間は約 1 秒しかかかりません。メモリであろうと時間であろうと、効率は要件を満たしています。ソートの最も良い点は、ソートする必要がないため、すべてのデータセットをメモリに読み込む必要がないことです。上記はデモンストレーション用であるため、500 万の要素がメモリ内に直接構築されていますが、データ構造の核心は次のとおりであるため、これをすべてファイルに転送して、1 行ずつ読み取って比較することができます。線形トラバーサルをメモリ内の非常に小さな上部ヒープ構造と比較し、最後に TopN を取得します。

---

終了

最後に言いたいのは、アルゴリズム + データ構造 が非常に重要であるということです。優れたアルゴリズムは大幅に改善できる可能性があります。私たちの効率。

以上がPHP ヒープが TopK アルゴリズムを実装する例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。