ホームページ >ウェブフロントエンド >CSSチュートリアル >CSS は任意のサイズ、方向、角度の矢印コードを実装します
CSS は任意のサイズ、方向、角度の矢印コードを実装します
- 小云云オリジナル
- 2018-03-06 09:33:374123ブラウズ
この記事では、CSS を使用して任意のサイズ、任意の方向、任意の角度の矢印を実現するための関連情報を主に紹介します。あなたを助けられる。
Web 開発では、ドロップダウン矢印

や右矢印

などの矢印がよく使用されます。 通常、これは CSS で実装されます:
{
display: inline-block;
margin: 72px;
border-top: 24px solid;
border-right: 24px solid;
width: 120px;
height: 120px;
transform: rotate(45deg);
}これは、p の border-top と border-right を使用して、p を回転することによって実現されるためです。
任意の角度の矢印
ここで質問があります: 120 度の角度の矢印が必要な場合はどうすればよいですか? border-top と border-right は常に 90 度であるため、回転だけでは機能しません。 まず p を 45 度回転してひし形にし、それを任意の角度まで引き伸ばすことで、任意の角度の矢印を得ることができます。回転とスケーリングの 2 つの変換が使用されるため、変換行列 transform:matrix(a,b,c,d,e,f) を使用する必要があります。 ここでの 6 つの変数は 3 次元の変換行列を形成しますtransform: matrix(a,b,c,d,e,f) 这个变换矩阵。 这里的6个变量组成了一个3介的变换矩阵
任意点p(x,y)的平移, 旋转, 伸缩变换以及他们的各种组合都可以通过这个变换矩阵做到:
注:这里用齐次坐标 来表达一个点。 简单说就是p(x, y) 表示为p'(x', y', 1)
平移矩阵
v(x, y) 沿着x轴平移tx, 沿着y轴平移ty。 则有:
x' = x + tx
y' = y + ty
所以平移矩阵:
旋转矩阵
v(x, y) 点绕原点旋转θ到v'(x', y')
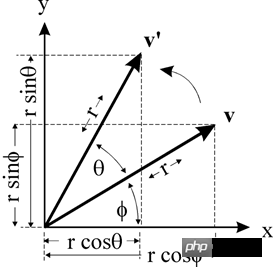
则有:
x = r * cos(ϕ )
y = r * sin(ϕ )x' = r * cos(θ + ϕ) = r * cos(θ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // 余弦公式
y' = r * sin(θ + ϕ) = r * sin(θ) * cos(ϕ) + r * cos(θ) * sin(ϕ ) // 正弦公式
所以:
x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos(θ)
所以旋转矩阵:
伸缩矩阵
假设x轴,y轴的伸缩率分别是kx, ky。 则有:
x' = x * kx
y' = y * ky
所以:
复合变换
如果是对p(x, y)先平移(变换矩阵A), 然后旋转(变换矩阵B), 然后伸缩(变换矩阵C)呢?
p' =C(B(Ap)) ==> p' = (CBA)p //矩阵乘法结合率
现在任意角度o的箭头就很简单了:
先把p旋转45度 成为 菱形, 变换为 M1 伸缩x轴, y轴 :
x' = size * cos(o/2) = x * √2 * cos(o/2) y' = size * sin(o/2) = y * √2 * sin(o/2)
即: kx = √2 * cos(o/2); ky = √2 * sin(o/2) 这样就得到了任意角度的箭头。 变换为 M2
如果箭头的方向不是指向右侧, 在进行一次旋转就可以得到任意方向的箭头。变换为 M3
那么由于 p' =C(B(Ap)) ==> p' = (CBA)p任意の点 p(x,y) の平行移動、回転、拡大変換、およびさまざまな組み合わせは、この変換行列を通じて実現できます:
v(x, y) は tx を x 軸に沿って平行移動し、ty を y 軸に沿って平行移動します。 次に、次のようになります:
x' = x + txy' = y + ty
したがって、変換行列:
回転行列
v(x, y) 点が回転します原点を中心にθをv'(x', y')に

Then:
x = r * cos(ϕ )つまり、y = r * sin(ϕ )
x' = r * cos(θ + ϕ) = r * cos(θ) * cos(ϕ ) - r * sin(θ) * sin(ϕ ) // コサインの公式y' = r * sin(θ + ϕ) = r * sin(θ) * cos(ϕ) + r * cos(θ ) * sin (ϕ ) // サインの公式
x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos (θ)
したがって、回転行列:
ストレッチ行列| x' = x * kx | y' = y * ky | つまり: | 複合変換 |
|---|---|---|---|
| p' =C(B(Ap)) ==> p' = (CBA)p //行列乗算の組み合わせ率 | さて、任意の角度 o の矢印は非常に単純です: | まず p を 45 度回転させて菱形にし、それを | M1 に変換しますx 軸、y 軸を伸縮します: |
npm install rc-arrow --save | つまり: kx = √ 2 * cos (o/2); ky = √2 * sin(o/2) これにより、任意の角度の矢印が得られます。 M2 | に変形 矢印の方向が右を向いていない場合は、回転を行うことで任意の方向に矢印を得ることができます。 | M3 |
| M2 | M1 を計算できます。 p に対応する変換を実行すると、任意の角度と方向の矢印を取得できます。pの幅と高さは矢印の辺の長さであり、調整することで任意の辺の長さの矢印を得ることができます。 | React コンポーネント | |
| 例 | 単純な矢印 |
安装使用
npm install rc-arrow --save
import Arrow from 'rc-arrow'
class Hw extends Component {
render() {
return (
<Arrow size="20px" color="red"/>
)
}
}相关推荐:
以上がCSS は任意のサイズ、方向、角度の矢印コードを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。


 y' = x * sin(θ) + y * cos (θ)
y' = x * sin(θ) + y * cos (θ)