ホームページ > 記事 > ウェブフロントエンド > Canvas がベジェ曲線を使用してポリラインセグメントを滑らかにフィットさせる方法の詳細な説明

Canvas がベジェ曲線を使用してポリラインセグメントを滑らかにフィットさせる方法の詳細な説明

小云云オリジナル: 2018-01-13 09:42:394067ブラウズ

この記事では、ベジェ曲線を使用してキャンバスに基づいてポリラインセグメントを滑らかにフィットさせる方法に関する関連情報を主に紹介します。編集者はそれが非常に優れていると考えたので、参考として共有します。編集者をフォローして見てみましょう。皆さんのお役に立てれば幸いです。

最初に書いてください

今回は、キャンバスに描画されたポリラインセグメントのエッジとコーナーを「滑らかにする」方法、つまり、各描画点にベジェ曲線を渡すことによって元のポリライングラフを置き換える方法を共有します。

なぜポリラインセグメントをスムーズにフィットさせる必要があるのですか

まず、Echarts での折れ線グラフのレンダリング効果を見てみましょう:

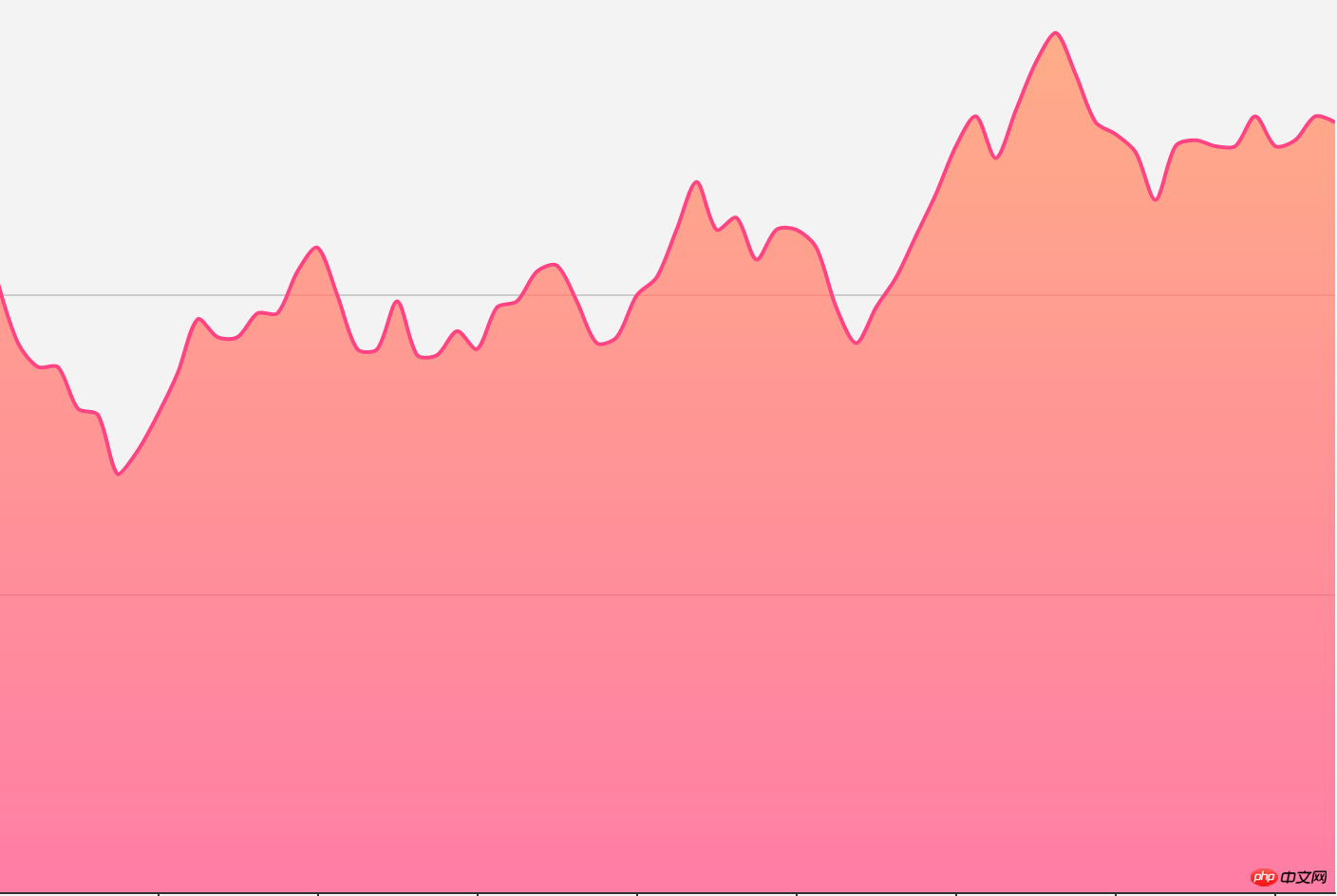
最初、私はこのポリラインセグメントが実際に曲線で通過したので、単純な点描画だとばかり思っていたので、最初に実装した「簡単（醜い）簡単（醜い）」バージョンは次のようになりました:

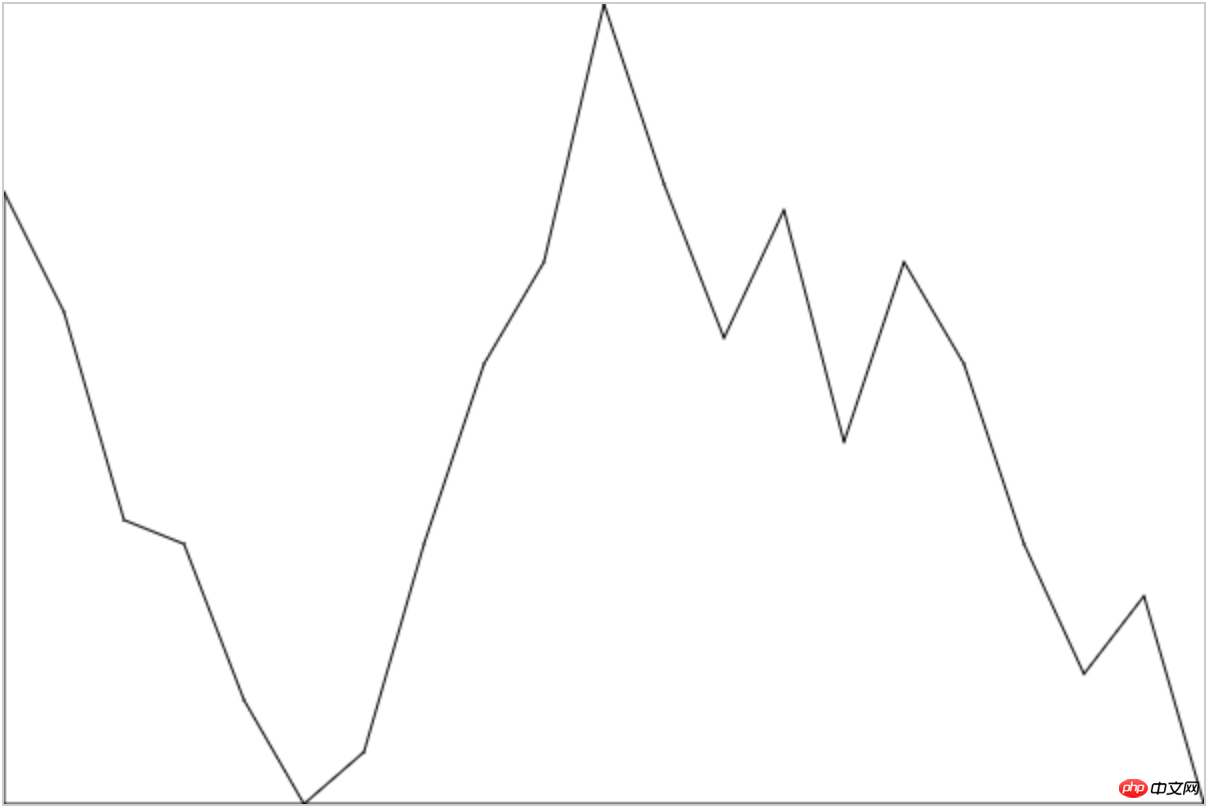
スタイルには注意しないでください重要なのは、実装後、Echarts で実装された描画ポイントが非常にスムーズであることがわかり、その後の議論のきっかけにもなりました。滑らかな曲線を定期的に描くにはどうすればよいですか?

レンダリング

まず、最終的な模倣の実装を見てみましょう:

それがEchartsの内部でどのように実装されているかわからないからです(escape

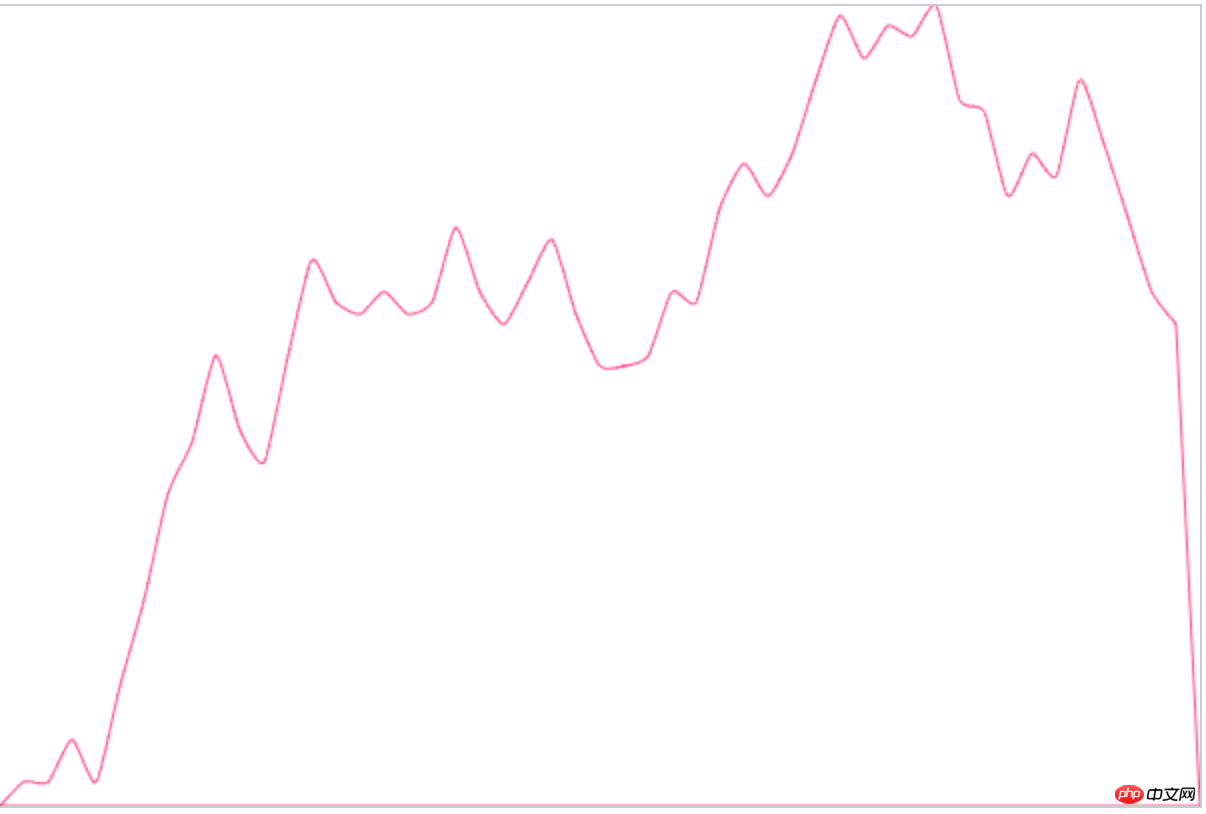
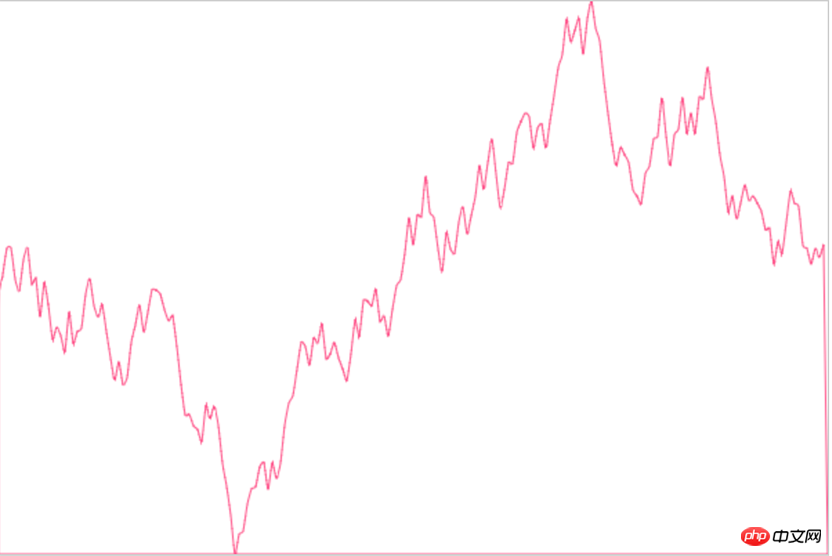
それは非常に丸みを帯びており、私たちのものと非常に一致しています)元のアイデア) 閉じて、曲線が描画点を通過するかどうかを確認してみましょう:

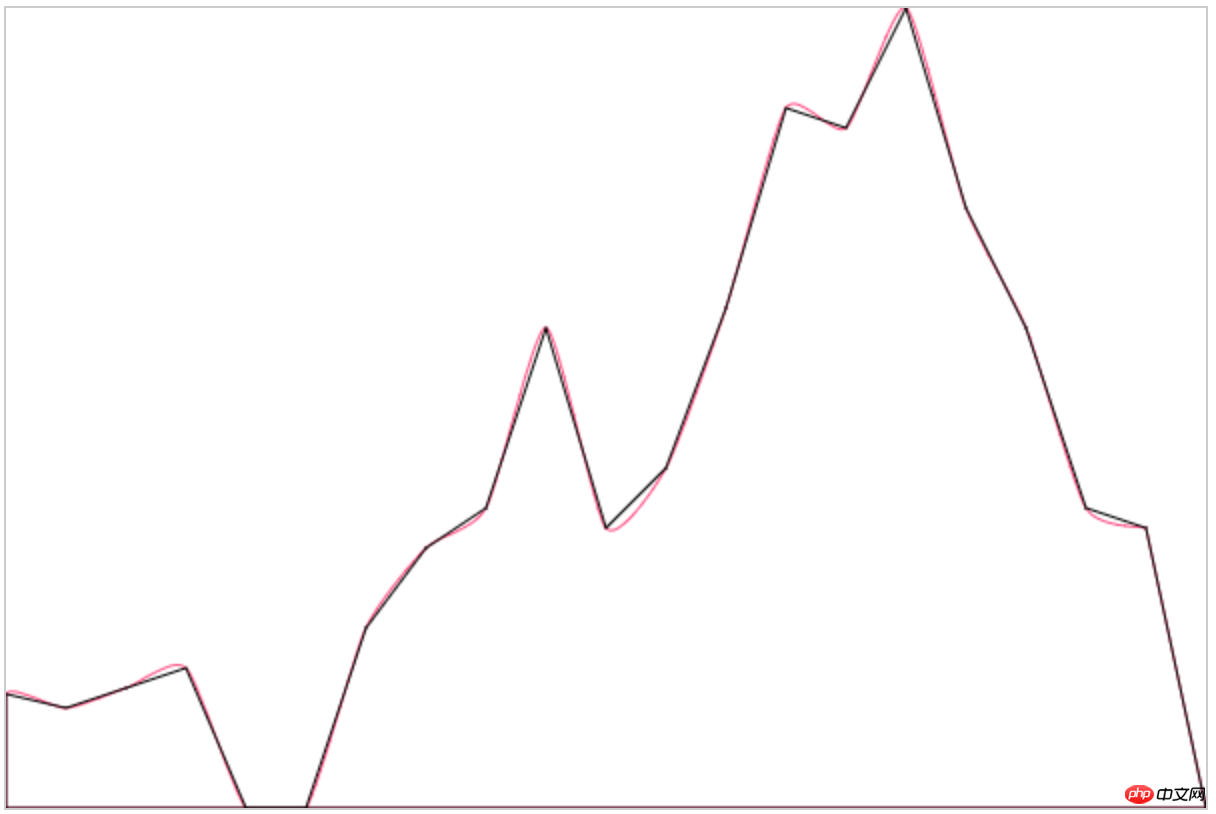
それでは、折れ線グラフを描画するための実装プロセスを見てみましょう

var data = [Math.random() * 300];
        for (var i = 1; i < 50; i++) { //按照echarts
            data.push(Math.round((Math.random() - 0.5) * 20 + data[i - 1]));
        }
        option = {
            canvas:{
                id: &#39;canvas&#39;
            },
            series: {
                name: &#39;模拟数据&#39;,
                itemStyle: {
                    color: &#39;rgb(255, 70, 131)&#39;
                },
                areaStyle: {
                    color: &#39;rgb(255, 158, 68)&#39;
                },
                data: data
            }
        };

折れ線グラフの描画

まず、使用するデータを配置するコンストラクタを初期化します:

function LinearGradient(option) {
    this.canvas = document.getElementById(option.canvas.id)
    this.ctx = this.canvas.getContext(&#39;2d&#39;)
    this.width = this.canvas.width
    this.height = this.canvas.height
    this.tooltip = option.tooltip
    this.title = option.text
    this.series = option.series //存放模拟数据
}

折れ線グラフの描画:

LinearGradient.prototype.draw1 = function() { //折线参考线
    ... 
    //要考虑到canvas中的原点是左上角，
    //所以下面要做一些换算，
    //diff为x,y轴被数据最大值和最小值的取值范围所平分的等份。
    this.series.data.forEach(function(item, index) {
        var x = diffX * index,
            y = Math.floor(self.height - diffY * (item - dataMin))
        self.ctx.lineTo(x, y) //绘制各个数据点
    })
    ...
}

ベジェ曲線滑らかなフィッティング

ベジェ曲線の重要なポイントは、制御点の選択です。この Web サイトでは、異なる制御点で描かれた異なる曲線を動的に表示できます。結局のところ、著者は Baidu を選択しました。結局のところ、彼は数学が苦手です:)。特定のアルゴリズムに興味がある学生は、それについてさらに詳しく学ぶことができます。次に、制御点の計算の結論について説明します。

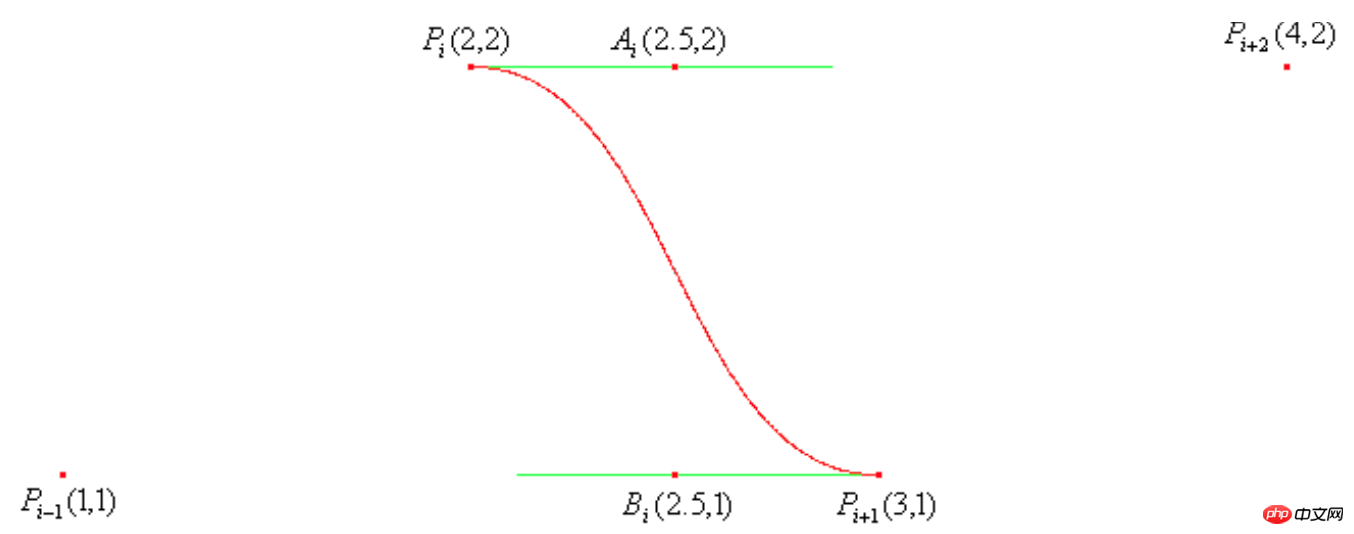
上の式には、現在の点、前の点、次の 2 点の 4 つの座標点が含まれます。座標値が下図に示すとおりである場合、描かれる曲線は次のようになります。

ただし、この式は始点と終点には使えないという問題がありますが、その記事では境界値を扱う方法も紹介しています:

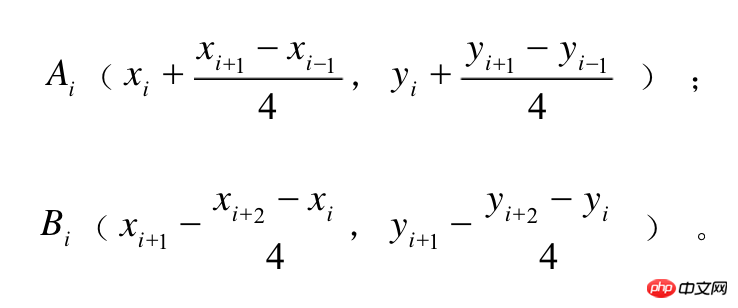
そこで、ポリラインを滑らかな曲線に変更するときは、境界値を変更すると、他の制御点が計算され、ベッセル関数に代入されて完了します:

//核心实现
this.series.data.forEach(function(item, index) { //找到前一个点到下一个点中间的控制点
    var scale = 0.1 //分别对于ab控制点的一个正数，可以分别自行调整
    var last1X = diffX * (index - 1),
        last1Y = Math.floor(self.height - diffY * (self.series.data[index - 1] - dataMin)),
        //前一个点坐标
        last2X = diffX * (index - 2),
        last2Y = Math.floor(self.height - diffY * (self.series.data[index - 2] - dataMin)),
        //前两个点坐标
        nowX = diffX * (index),
        nowY = Math.floor(self.height - diffY * (self.series.data[index] - dataMin)),
        //当期点坐标
        nextX = diffX * (index + 1),
        nextY = Math.floor(self.height - diffY * (self.series.data[index + 1] - dataMin)),
        //下一个点坐标
        cAx = last1X + (nowX - last2X) * scale,
        cAy = last1Y + (nowY - last2Y) * scale,
        cBx = nowX - (nextX - last1X) * scale,
        cBy = nowY - (nextY - last1Y) * scale 
    if(index === 0) {
        self.ctx.lineTo(nowX, nowY)
        return
    } else if(index ===1) {
        cAx = last1X + (nowX - 0) * scale
        cAy = last1Y + (nowY - self.height) * scale 
    } else if(index === self.series.data.length - 1) {
        cBx = nowX - (nowX - last1X) * scale
        cBy = nowY - (nowY - last1Y) * scale
    } 
        self.ctx.bezierCurveTo(cAx, cAy, cBx, cBy, nowX, nowY);
        //绘制出上一个点到当前点的贝塞尔曲线
    })

毎回通過する点は現在の点ですが、記事に記載されている式は計算で分かることです次の点制御点アルゴリズムなので、コード実装では、すべての点の計算を前の点に移動しました。インデックス = 0 (初期点) の場合、前の点から現在の点まで曲線を描いており、描く必要のある 0 への曲線がないため、曲線を描く必要はありません。インデックス = 1 から開始して、通常どおり 0 から 1 まで曲線の描画を開始できます。インデックス = 1 の場合、その前に 2 番目の点がないため、それは境界値点となり、特別な計算が必要になります。ワンポイント。残りは通常の公式に従って計算でき、AB の xy 座標がベッセル関数に代入されます。

Canvas がベジェ曲線を使用してポリライン セグメントを滑らかにフィットさせる方法の詳細な説明

関連記事

Canvas がベジェ曲線を使用してポリラインセグメントを滑らかにフィットさせる方法の詳細な説明