線形テーブルの原理と簡単な実装方法の詳細な分析

以下のエディターでは、線形テーブルの原理と簡単な実装方法について簡単に説明します。編集者はこれがとても良いと思ったので、参考として共有します。エディターで見てみましょう

1. 線形テーブル

原則: 0 個以上の類似したデータ要素の有限シーケンス

原則:

特徴:

1 . 秩序性

2. 有限性

3. 同じタイプの要素

4. 最初の要素には先行要素がなく、最後の要素には先行要素と後続要素があります

論理データ構造。通常、シーケンシャル実装とリンク リスト実装の 2 つがあります。 2. 配列ベースのリニア テーブル シーケンシャル実装。原則として、リニア テーブル データ要素を格納します。

原理図:

アルゴリズム原理:

1. 要素を格納するためのストレージサイズの固定長配列空間を初期化します

2. 配列を通じて要素に素早くアクセスします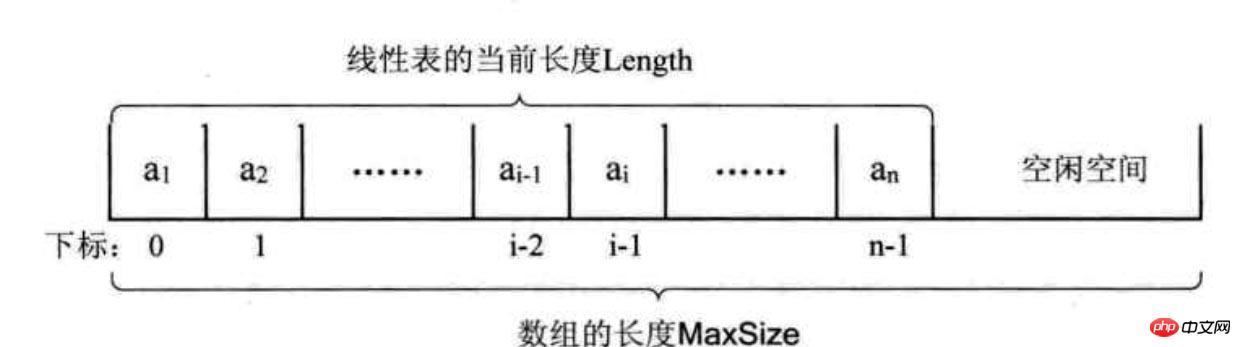

3.要素の挿入と削除を実装します

概要:

1. テーブル内の要素間の論理関係を表現するために追加の記憶域を追加する必要はありません

2。 table 3. 挿入と削除には配列のコピー (つまり、多数の要素の移動) が必要です 4. 線形テーブルの長さが大幅に変化すると、頻繁な拡張が必要になり、記憶域の断片化が発生します

コード:

インターフェース定義:

package online.jfree.base;

/**
 * author : Guo LiXiao
 * date : 2017-6-14 11:46
 */

public interface LineList <E>{

 /**
  * lineList 是否为空
  * @return
  */
 boolean isEmpty();

 /**
  * 清空 lineList
  */
 void clear();

 /**
  * 获取指定位置元素
  * @param index
  * @return
  */
 E get(int index);

 /**
  * 获取元素第一次出现的位置
  * @param e
  * @return
  */
 int indexOf(E e);

 /**
  * 判断 lineList是否包含指定元素
  * @param e
  * @return
  */
 boolean contains(E e);

 /**
  * 设置指定位置数据，如数据已存在 则覆盖原数据
  * @param index
  * @param e
  * @return
  */
 E set(int index, E e);

 /**
  * 移除指定位置元素
  * @param index
  * @return
  */
 E remove(int index);

 /**
  * 在lineList结尾插入元素
  * @param e
  * @return
  */
 E add(E e);

 /**
  * 在index后面插入元素
  * @param index
  * @param e
  * @return
  */
 E add(int index, E e);

 /**
  * 返回lineList长度
  * @return
  */
 int size();



}

アルゴリズム実装:

package online.jfree.base;

/**
 * author : Guo LiXiao
 * date : 2017-6-15 13:44
 */

public class OrderedLineList<E> implements LineList<E> {

 private static final int INIT_CAPACITY = 10;

 private transient E[] elementData;

 private transient int elementLength;

 private int size;

 public OrderedLineList() {
  this(0);
 }

 public OrderedLineList(int initCapacity) {
  init(initCapacity);
 }

 private void init(int initCapacity) {
  if (initCapacity >= 0) {
   this.elementData = (E[]) new Object[initCapacity];
   this.elementLength = initCapacity;
  } else {
   throw new IllegalArgumentException("Illegal Capacity: " +
     initCapacity);
  }
  this.size = 0;
 }

 /**
  * 扩容
  */
 private void dilatation() {
  int oldCapacity = this.elementLength;
  int newCapacity = oldCapacity;
  if (oldCapacity <= this.size) {
   newCapacity = oldCapacity + INIT_CAPACITY;
  }else if(oldCapacity - INIT_CAPACITY > this.size){
   newCapacity = oldCapacity - INIT_CAPACITY;
  }
  if (oldCapacity != newCapacity){
   E[] newElementData = (E[]) new Object[newCapacity];
   System.arraycopy(elementData, 0, newElementData, 0, oldCapacity);
   this.elementLength = newCapacity;
   this.elementData = newElementData;
  }
 }

 /**
  * 校验列表索引越界
  * @param index
  */
 private void checkCapacity(int index){
  if (index > this.size - 1 || index < 0)
   throw new IndexOutOfBoundsException(new StringBuffer("[index : ").append(index).append("] , [size : ").append(size).append("] ").toString());
 }

 @Override
 public boolean isEmpty() {
  return this.size == 0;
 }

 @Override
 public void clear() {
  this.init(0);
 }

 @Override
 public E get(int index) {
  this.checkCapacity(index);
  return this.elementData[index];
 }

 @Override
 public int indexOf(E e) {
  for (int i = 0; i < this.size; i++){
   if (e == null && elementData[i] == null || e.equals(elementData[i])){
    return i;
   }
  }
  return -1;
 }

 @Override
 public boolean contains(E e) {
  return this.indexOf(e) > 0;
 }

 @Override
 public E set(int index, E e) {
  this.checkCapacity(index);
  this.dilatation();
  E oldElement = this.elementData[index];
  this.elementData[index] = e;
  return oldElement;
 }

 @Override
 public E remove(int index) {
  this.dilatation();
  E e = elementData[index];
  if (index == size - 1) elementData[index] = null;
  else {
   int length = size - index - 1;
   System.arraycopy(elementData, index + 1, elementData, index, length);
  }
  size --;
  return e;
 }

 @Override
 public E add(E e) {
  return this.add(size, e);
 }

 @Override
 public E add(int index, E e) {
  this.dilatation();
  if (index == size) elementData[index] = e;
  else {
   index++;
   int lastLength = size - index;
   E[] lastElementData = (E[]) new Object[lastLength];
   System.arraycopy(elementData, index, lastElementData, 0, lastLength);
   elementData[index] = e;
   System.arraycopy(lastElementData, 0, elementData, index + 1, lastLength);
  }
  size ++ ;
  return e;
 }

 @Override
 public int size() {
  return this.size;
 }

}

以上が線形テーブルの原理と簡単な実装方法の詳細な分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。