ホームページ >ウェブフロントエンド >jsチュートリアル >バブルソーティング法の詳しい説明
バブルソーティング法の詳しい説明
- 一个新手オリジナル
- 2017-10-06 10:41:442879ブラウズ
バブルソート法
HTML5 Academy-Coder: この号では引き続き、アルゴリズムであるバブルソート法を紹介します。バブルソートのアルゴリズムは比較的シンプルで使いやすく、比較的安定しているため、面接官からよく質問されるアルゴリズムの一つです。
ヒント:「アルゴリズム」と「並べ替え」の基礎知識は、前回の「選択範囲の並べ替え方法」で詳しく説明していますので、記事の最後にある該当記事のリンクをクリックしてご覧ください。ここで繰り返さないでください。
バブルソートの原理
基本原則
シーケンスの先頭からトラバースを開始し、2つずつ比較し、前者が後者より大きい場合、最大の番号(このソートの最大の番号)まで位置を交換します。最終的に、順序付けされていないシーケンスの最後にスワップされ、順序付けされたシーケンスの一部になります
次回走査するとき、以前の各走査後の最大数は並べ替えに参加しなくなります
この操作を複数回繰り返します。シーケンスのソートが完了するまで。
並べ替えの過程で、小さな数字が常に前方に配置され、大きな数字が後方に配置されるため、泡が徐々に上に浮き上がっていくように見えるため、バブルソートと呼ばれます。
原理図
ヒント: 青はソートのラウンドで交換を待っていることを表し、黒はこのラウンドのソートで交換が完了したことを表し、赤はソートが完了したことを表します
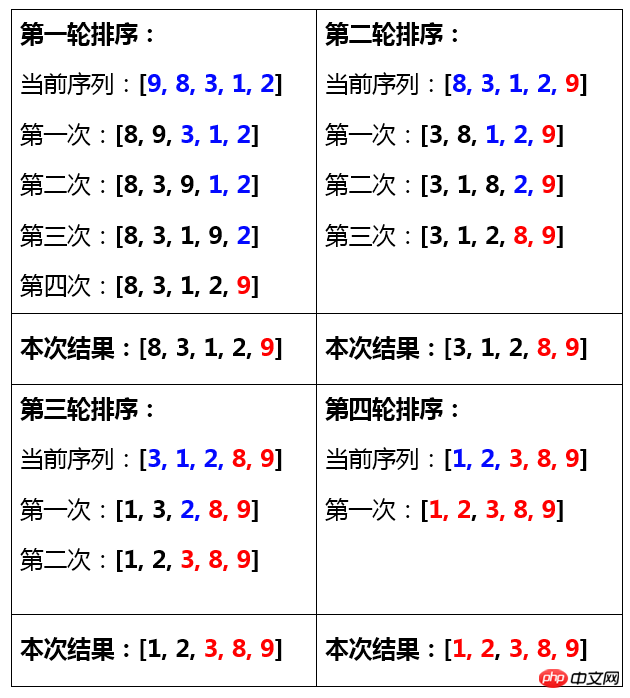
バブリングステップ分解
ループに使用ソートの回数を決定します
ソートする数列に数字が1つだけ残っている場合は順序が決定できるため、ソートする必要はありません。したがって、ソートの数は、数列の長さ – 1になります。

各並べ替えの比較数を制御します
各並べ替えでは、シーケンス内の複数の数値をペアで比較する必要があり、for ステートメントを使用して複数の比較を実装する必要があります。この for ループは、ソートされた回数の for ループ内にネストされます (二重 for のネストを形成します)。

ヒント: j は len - i - 1 より小さい値に設定する必要があります。i を減算する理由は、並べ替えられた数値が比較に関与しなくなるためです。1 を減算する理由は、配列の添え字インデックスであるためです。値は 0 から始まります。
コア機能 - 状況に応じてペアを比較し、位置を交換します
2 つの数値の大きさを比較し、前者が後者より大きい場合、値を交換します。つまり、位置を交換します。

バブルソート法の完全なコード

バブルソート法の最適化
シーケンスのデータが: [0, 1, 2, 3, 4, 5];
上記を使用するバブルソート法 バブルソートで得られた結果には全く問題はありませんが、ソートする順番は決まっており、理論的にはソートを横断する必要はありません。
現在のアルゴリズムは、初期シーケンスが正しいかどうかに関係なくトラバーサルソートを実行し、効率が比較的低いため、現在のソートアルゴリズムを最適化する必要があります。
次のアルゴリズムでは、各並べ替えの前にスワップ変数が導入され、false に初期化されます。2 つの数値の位置が入れ替わる場合は、それを true に設定します。
各ソートの最後に、swap が false であるかどうかを判断します。 false である場合は、シーケンスがソートされたか、シーケンス自体が順序付けされたシーケンスであることを意味し、次のソートは実行されません。
この方法により、不必要な比較と位置交換が削減され、アルゴリズムのパフォーマンスがさらに向上します。

バブルソート法の効率
時間計算量
最良の状態: ソートされるシーケンス自体は順序付けされたシーケンスであるため、最適化されたコードによれば、ソート回数は n-1 回であると結論付けることができます。 、および時間 複雑さは O(n);
最悪の場合: ソートされるシーケンスは逆の順序であり、1 + 2 +3...(n - 1) = n(n - 1)/2 回
時間計算量は O(n^2) です。
空間複雑度
バブルソート法では要素の位置を交換するために余分な空間(一時変数)が必要なため、空間複雑度はO(1)です。
アルゴリズムの安定性
隣接する要素が等しい場合、位置を入れ替える必要がなく、同じ要素の順序が変わらないため、安定したソートとなります。
Oって何ですか? !
時間計算量は、より正確には、問題のサイズが増大し続けるときのアルゴリズムの時間増加曲線を表します。したがって、これらの桁違いの増加は正確なパフォーマンス評価ではなく、近似値として理解することができます。 (空間計算量も同様)
O(n?) は、n が大きい場合、計算量は Cn? にほぼ等しいことを意味します。簡単に言えば、n が十分に大きい場合、n は線形になるためです。成長の複雑さは二次関数的に増大します。
O(n) は、n が非常に大きい場合、複雑さは Cn にほぼ等しく、C は特定の定数であることを意味します。つまり、n が線形に増加するにつれて、複雑さも線形スケールに沿って増加します。
O(1) は、n が大きい場合、基本的に複雑さは増加しないことを意味します。つまり、n が線形に増加するため、複雑さは n の影響を受けず、一定のレベル (ここでの定数は 1) に沿って増加します。
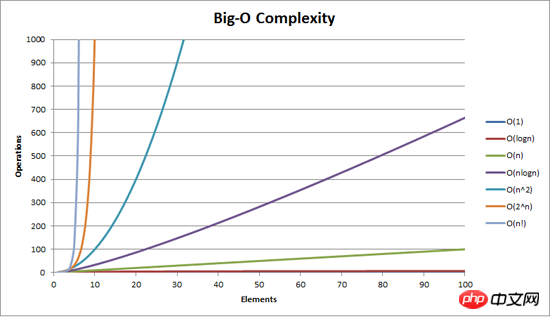
ヒント: 写真では、O(1) が X 軸に近いため、はっきりと見えません。
ヒント: この写真は「Stack Overflow」Web サイトからのものです。
関連記事へのリンク
並べ替え方法を選択
毎日幸せに
人生は大変でコーディングは簡単ではありませんが、笑顔を忘れないでください!

以上がバブルソーティング法の詳しい説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

