Python で実装された 8 つの並べ替えアルゴリズムの概要 (パート 1)

この記事では、主に Python で実装された 8 つのソート アルゴリズムの最初の部分を詳しく紹介します。興味のある方は参考にしてください。

ソートは、コンピューターで頻繁に実行されるタスクです。 「順序なし」レコード シーケンスのセットを「順序付き」レコード シーケンスに調整します。内部仕分けと外部仕分けに分かれます。ソートプロセス全体が外部メモリにアクセスせずに完了できる場合、このタイプのソート問題は内部ソートと呼ばれます。逆に、ソートに参加するレコードの数が多く、シーケンス全体のソート処理がメモリ内で完全に完了できず、外部メモリへのアクセスが必要な場合、この種のソート問題は外部ソートと呼ばれます。内部ソートのプロセスは、順序付けられたレコードのシーケンスの長さを徐々に拡張するプロセスです。

理解をより明確かつ深くするために、図を見てください:

並べ替えられるレコード シーケンスに同じキーワードを持つ複数のレコードがあり、並べ替えても、これらのレコードの相対的な順序は変わらないと仮定します。元のシーケンスでは ri=rj であり、ri は rj より前にあり、ソートされたシーケンスでは ri は依然として rj より前にある場合、このソート アルゴリズムは安定と呼ばれ、それ以外の場合は不安定と呼ばれます。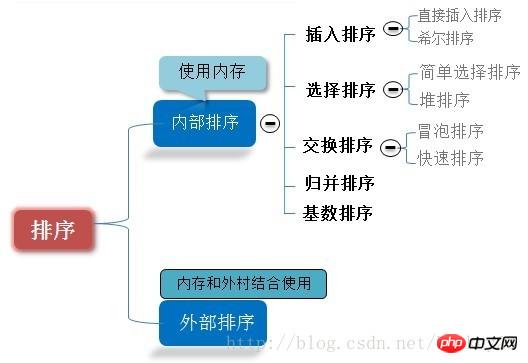

一般的なソートアルゴリズム

クイックソート、ヒルソート、ヒープソート、直接選択ソートは安定したソートアルゴリズムではありませんが、基数ソート、バブルソート、直接挿入ソート、半挿入ソート、マージソートは安定したソートアルゴリズムです。アルゴリズム

この記事では、Python を使用して、バブル ソート、挿入ソート、ヒル ソート、クイック ソート、直接選択ソート、ヒープ ソート、マージ ソート、基数ソートの 8 つのソート アルゴリズムを実装します。

1. バブルソート

アルゴリズム原理:

順序付けされていないデータのセット a[1]、a[2]、...a[n] がわかっており、昇順に並べる必要があります。まず、a[1] と a[2] の値を比較します。a[1] が a[2] より大きい場合は、2 つの値を交換します。そうでない場合は、値は変更されません。次に、a[2] と a[3] の値を比較します。a[2] が a[3] より大きい場合は、2 つの値を交換します。そうでない場合は、値は変更されません。次に、a[3] と a[4] などを比較し、最後に a[n-1] と a[n] の値を比較します。 1 ラウンドの処理の後、a[n] の値はこのデータ セット内で最大になる必要があります。 a[1]～a[n-1]を再度同様に処理すると、a[n-1]の値はa[1]～a[n-1]の中で最大でなければなりません。次に、a[1]~a[n-2]を同様に 1 ラウンド処理します。合計 n-1 回の処理の後、a[1]、a[2]、...a[n] が昇順に配置されます。降順ソートは、a[1] が a[2] より小さい場合、2 つの値が交換され、それ以外の場合は変更されません。 一般に、ソートの各ラウンドの後、最大 (または最小) の数値がデータ シーケンスの最後に移動され、理論的には合計 n(n-1)/2 回の交換が実行されます。

長所: 安定しています。
短所: 遅い、一度に移動できる隣接するデータは 2 つだけです。

Pythonコードの実装:

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
 lstlen = len(lst1);i = 0
 while i < lstlen:
  for j in range(1,lstlen):
   if lst1[j-1] > lst1[j]:
   #对比相邻两个元素的大小，小的元素上浮
    lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
  i += 1
  print &#39;sorted{}: {}&#39;.format(i, lst1)
 print &#39;-------------------------------&#39;
 return lst1
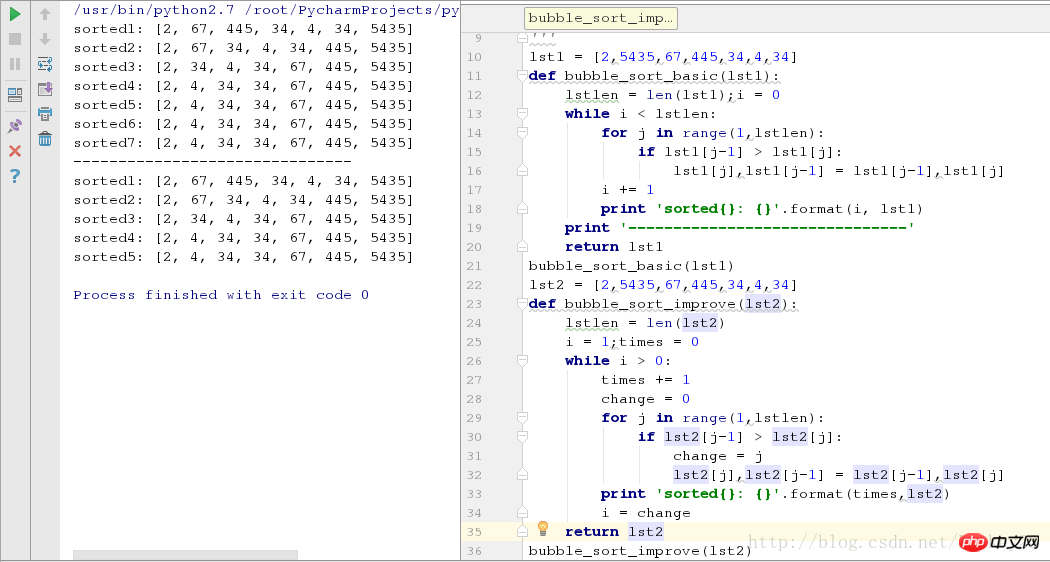
bubble_sort_basic(lst1)

バブルソートアルゴリズムの改善

完全に無秩序なシーケンス、または繰り返し要素がないシーケンスの場合、上記のアルゴリズムには同じ考え方で改善の余地はありませんが、シーケンス内に繰り返しの要素がある場合、またはいくつかの要素が順番に並んでいる場合、必然的に並べ替え処理にシンボリック変数の変更を追加して、特定の並べ替え処理をマークすることができます。あるソート処理中にデータの交換がなかった場合は、必要なデータが配置されたことを意味し、不要な比較処理を避けるためにソートをすぐに終了できます。 改良されたサンプルコードは次のとおりです。

lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
 lstlen = len(lst2)
 i = 1;times = 0
 while i > 0:
  times += 1
  change = 0
  for j in range(1,lstlen):
   if lst2[j-1] > lst2[j]:
   #使用标记记录本轮排序中是否有数据交换
    change = j
    lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
  print 'sorted{}: {}'.format(times,lst2)
  #将数据交换标记作为循环条件，决定是否继续进行排序
  i = change
 return lst2
bubble_sort_improve(lst2)

2 つのケースで実行中のスクリーンショットは次のとおりです。

上の図からわかるように、いくつかの要素が順番に配置されているシーケンスでは、最適化されたアルゴリズムにより 2 ラウンドのソートが削減されます。

2. 選択ソート

アルゴリズム原理:

各パスで、ソート対象のデータ要素から最小 (または最大) の要素が選択され、最後にすべてがソートされた順序で配置されます。ソート対象のデータ要素を並べます。

n 個のレコードを持つファイルの直接選択ソートは、n-1 個の直接選択ソートを通じて順序付けされた結果を取得できます: ①初期状態: 順序付けされていない領域は R[1..n] で、順序付き領域は空です。

②最初のソートパス

無順序領域R[1..n]内のキーワードが最も小さいレコードR[k]を選択し、それを無順序領域の最初のレコードR[1]と交換すると、R[1 ..1] と R[2..n] は、それぞれレコード数が 1 増加した新しい順序付き領域と、レコード数が 1 減った新しい非順序領域になります。

...

③ i 回目のソート
i 回目のソートが開始されると、現在の順序付き領域と順序なし領域はそれぞれ R[1..i-1] と R(1≤i≤n-1) になります。このソート操作は、現在の不規則領域から最小のキーを持つレコード R[k] を選択し、それを不規則領域の最初のレコード R と交換し、R[1..i] と R がそれぞれレコード番号になります。新しい順序付けされた領域の数は 1 増加し、レコードの数は 1 つ減少します。新しい順序付けされていない領域。

このようにして、n 個のレコードを持つファイルの直接選択ソートは、n-1 個の直接選択ソート パスを通じて順序付けされた結果を取得できます。

优点：移动数据的次数已知（n-1次）；
缺点：比较次数多，不稳定。

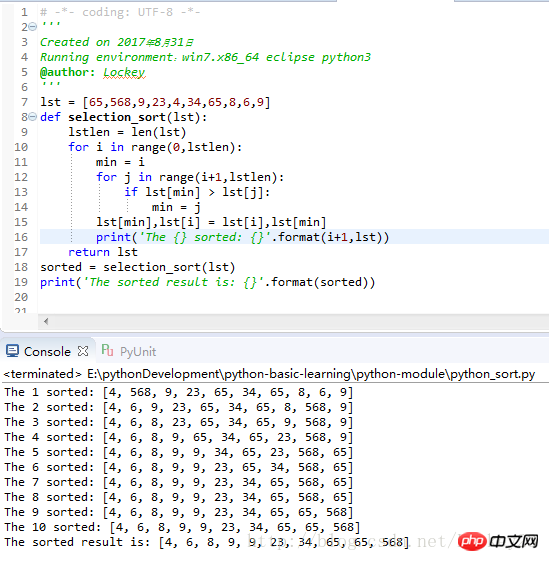
python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
 lstlen = len(lst)
 for i in range(0,lstlen):
  min = i
  for j in range(i+1,lstlen):
  #从 i+1开始循环遍历寻找最小的索引
   if lst[min] > lst[j]:
    min = j
  lst[min],lst[i] = lst[i],lst[min]
  #一层遍历结束后将最小值赋给外层索引i所指的位置，将i的值赋给最小值索引  
  print('The {} sorted: {}'.format(i+1,lst))
 return lst
sorted = selection_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

3. 插入排序

算法原理：

已知一组升序排列数据a[1]、a[2]、……a[n]，一组无序数据b[1]、b[2]、……b[m]，需将二者合并成一个升序数列。首先比较b[1]与a[1]的值，若b[1]大于a[1]，则跳过，比较b[1]与a[2]的值，若b[1]仍然大于a[2]，则继续跳过，直到b[1]小于a数组中某一数据a[x]，则将a[x]~a[n]分别向后移动一位，将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。（若无数组a，可将b[1]当作n=1的数组a）
优点：稳定，快；
缺点：比较次数不一定，比较次数越多，插入点后的数据移动越多，特别是当数据总量庞大的时候，但用链表可以解决这个问题。

算法复杂度

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。

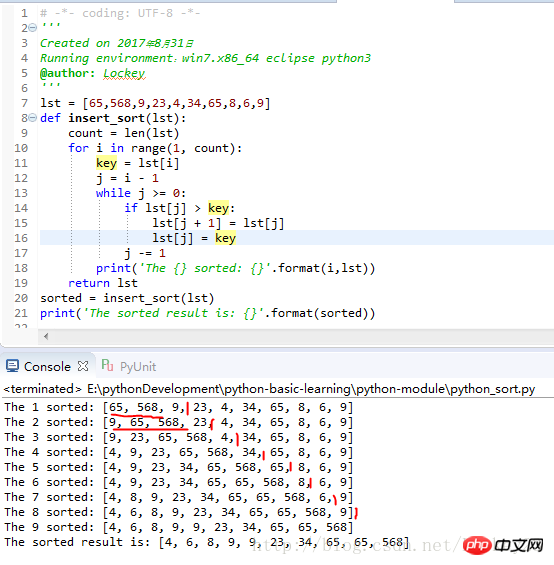
python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
 count = len(lst)
 for i in range(1, count):
  key = lst[i]
  j = i - 1
  while j >= 0:
   if lst[j] > key:
    lst[j + 1] = lst[j]
    lst[j] = key
   j -= 1
  print('The {} sorted: {}'.format(i,lst))
 return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

由排序过程可知，每次往已经排好序的序列中插入一个元素，然后排序，下次再插入一个元素排序。。。直到所有元素都插入，排序结束

4. 希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

算法原理

算法核心为分组（按步长）、组内插入排序

已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。发现当n不大时，插入排序的效果很好。首先取一增量d(d

python代码实现：

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
 print 'orginal list is {}'.format(lst)
 count = len(lists)
 step = 2
 times = 0
 group = int(count/step)
 while group > 0:
  for i in range(0, group):
   times += 1
   j = i + group
   while j < count:
    k = j - group
    key = lists[j]
    while k >= 0:
     if lists[k] > key:
      lists[k + group] = lists[k]
      lists[k] = key
     k -= group
    j += group
    print &#39;The {} sorted: {}&#39;.format(times,lists)
  group = int(group/step)
 print &#39;The final result is: {}&#39;.format(lists)
 return lists
shell_sort(lst)

运行测试结果截图：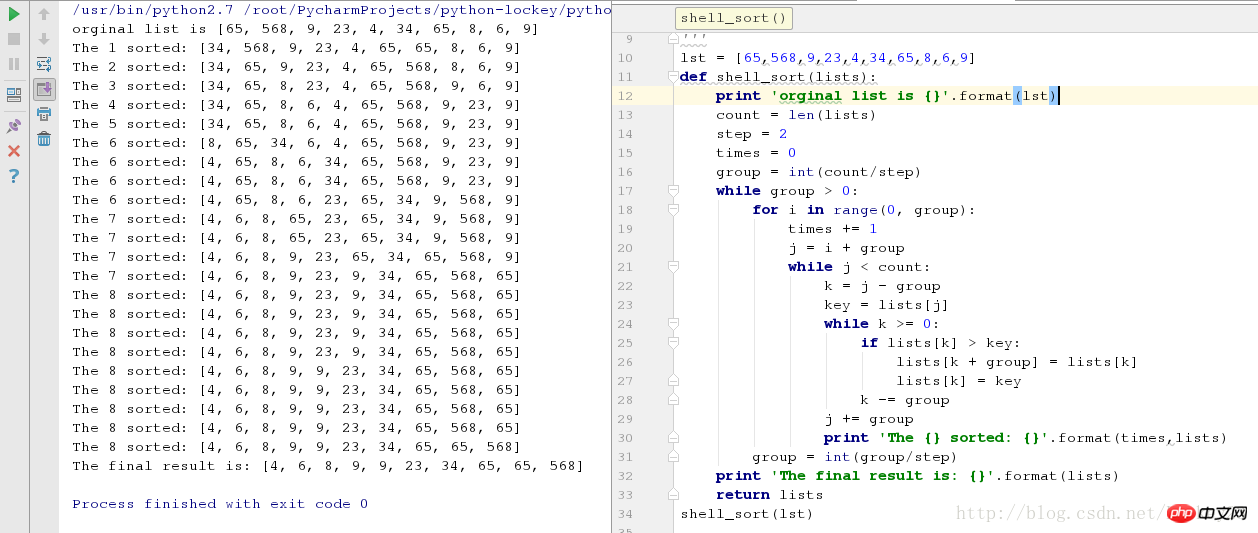

过程分析：

第一步：

1-5：将序列分成了5组（group = int(count/step)）,如下图，一列为一组：

然后各组内进行插入排序，经过5（5组*1次）次组内插入排序得到了序列：

The 1-5 sorted：[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步：

6666-7777：将序列分成了2组（group = int(group/step)）,如下图，一列为一组：

 

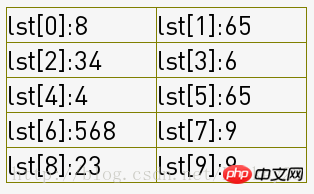
然后各组内进行插入排序，经过8（2组*4次）次组内插入排序得到了序列：

The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步：

888888888：对上一个排序结果得到的完整序列进行插入排序：

[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

经过9（1组*10 -1）次插入排序后：

The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]

ヒルソート適時性分析は、キーコード比較の数と記録された手の数は、増分因子シーケンスの選択に依存しますが、特定の状況下では、キーコードの比較の数と記録された手の数を正確に推定できます。 。最良の増分因子シーケンスを選択する方法をまだ誰も示していません。インクリメンタルファクターの並びは奇数や素数など様々な取り方が可能ですが、インクリメンタルファクター間には1以外の共通因子はなく、最後のインクリメンタルファクターは1でなければならないことに注意してください。丘選別法は不安定な選別法です

以上がPython で実装された 8 つの並べ替えアルゴリズムの概要 (パート 1)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。