バックトラッキング手法のサブセット ツリー テンプレートを使用して階段登りの問題を解決する Python の詳細な例

この記事では、階段登り問題を解決するための Python のバックトラッキング メソッド サブセット ツリー テンプレートの使用方法を主に紹介し、階段登り問題を簡単に説明し、例と組み合わせて、階段登りを解決するための Python のバックトラッキング メソッド サブセット ツリー テンプレートに関連する操作スキルを提供します。問題を必要とする友人は以下を参照してください

この記事の例では、Python がバックトラッキング メソッドのサブセット ツリー テンプレートを使用して階段登り問題を解決する方法について説明します。参考のために皆さんと共有してください。詳細は次のとおりです。

問題

ある階段には n 段あり、各段は 1 歩か 2 歩しか進むことができません。階段を下から上へ登る方法は何通りありますか?

分析

この問題は、分割統治法を使用する前に解決されています。ただし、ここではバックトラッキング サブセット ツリー テンプレートを使用してそれを解決します。

要素状態空間解析手法を紹介します。各ステップが要素であり、可能なステップの数 [1, 2] がその状態空間です。要素は固定されていませんが、状態空間は固定されていることがわかります。

コードに直接移動します。

コード

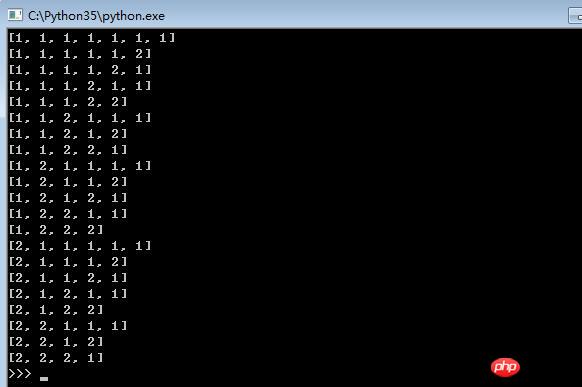
'''爬楼梯'''
n = 7 # 楼梯阶数
x = []  # 一个解（长度不固定，1-2数组，表示该步走的台阶数）
X = []  # 一组解
# 冲突检测
def conflict(k):
  global n, x, X
  # 部分解步的步数之和超过总台阶数
  if sum(x[:k+1]) > n:
    return True
  return False # 无冲突
# 回溯法（递归版本）
def climb_stairs(k): # 走第k步
  global n, x, X
  if sum(x) == n: # 已走的所有步数之和等于楼梯总台阶数
    print(x)
    #X.append(x[:]) # 保存（一个解）
  else:
    for i in [1, 2]: # 第k步这个元素的状态空间为[1,2]
      x.append(i)
      if not conflict(k): # 剪枝
        climb_stairs(k+1)
      x.pop()       # 回溯
# 测试
climb_stairs(0) # 走第0步

レンダリング

以上がバックトラッキング手法のサブセット ツリー テンプレートを使用して階段登りの問題を解決する Python の詳細な例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。