ホームページ >バックエンド開発 >Python チュートリアル >バックトラッキング手法のサブセット ツリー テンプレートに基づいて Python で 8 クイーン問題を解く
バックトラッキング手法のサブセット ツリー テンプレートに基づいて Python で 8 クイーン問題を解く
- 巴扎黑オリジナル
- 2017-09-02 11:52:421516ブラウズ
この記事では主に、バックトラッキング手法のサブセット ツリー テンプレートに基づいて 8 クイーンズ問題を実装するための Python を紹介します。8 クイーンズ問題の原理を簡単に説明し、問題を解決するための Python バックトラッキング手法のサブセット ツリー テンプレートの具体的な実装スキルを分析します。例の形式での 8 クイーン問題 必要なもの 友人が参照できるようにします
この記事では、バックトラッキング手法のサブセット ツリー テンプレートに基づいて 8 クイーン問題を実装する Python の例について説明します。詳細は次のとおりです:
問題
互いに攻撃できないように、つまり、2 つのクイーンが同じになることができないように、8 × 8 のグリッドのチェスに配置します。行または列、または同じ対角線上に何通りあるかを尋ねます。

分析
問題を単純化するために、8 つのクイーンが異なる行にあることを考慮し、各行に 1 つのクイーンを配置し、各行のクイーンを列 0、1、 2,..., 7, 各行の女王には 8 つの状態があると考えられます。次に、行 0 から始めて上から下にサブセット ツリー テンプレートを適用し、各行のクイーンの 8 つの状態をたどるだけです。
コード:
'''
8皇后问题
'''
n = 8
x = [] # 一个解(n元数组)
X = [] # 一组解
# 冲突检测:判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
global x
for i in range(k): # 遍历前 x[0~k-1]
if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k): # 判断是否与 x[k] 冲突
return True
return False
# 套用子集树模板
def queens(k): # 到达第k行
global n, x, X
if k >= n: # 超出最底行
#print(x)
X.append(x[:]) # 保存(一个解),注意x[:]
else:
for i in range(n): # 遍历第 0~n-1 列(即n个状态)
x.append(i) # 皇后置于第i列,入栈
if not conflict(k): # 剪枝
queens(k+1)
x.pop() # 回溯,出栈
# 解的可视化(根据一个解x,复原棋盘。'X'表示皇后)
def show(x):
global n
for i in range(n):
print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))
# 测试
queens(0) # 从第0行开始
print(X[-1], '\n')
show(X[-1])レンダリング
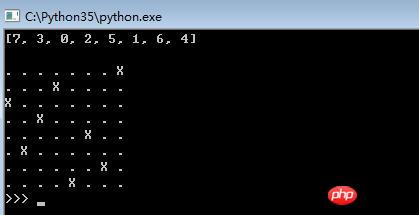
以上がバックトラッキング手法のサブセット ツリー テンプレートに基づいて Python で 8 クイーン問題を解くの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

