Python で一般的に使用される基本的なアルゴリズム
- 巴扎黑オリジナル
- 2017-08-02 10:27:413300ブラウズ
この記事では主に Python で一般的に使用されるアルゴリズムについて学習します。興味のある方は、このセクションの内容を参照してください。
アルゴリズムの定義時間計算量
空間計算量 一般的に使用されるアルゴリズムの例
1. アルゴリズムの定義
アルゴリズム (アルゴリズム) は、問題を解決するための一連の明確な指示を指します。問題の解決策を説明すること。つまり、一定の標準化されたインプットに対して、限られた時間内で必要なアウトプットを得ることが可能です。アルゴリズムに欠陥があるか、問題に対して不適切な場合、そのアルゴリズムを実行しても問題は解決されません。アルゴリズムが異なると、同じタスクを完了するために使用する時間、空間、効率が異なる場合があります。アルゴリズムの品質は、空間の複雑さと時間の複雑さによって測定できます。 アルゴリズムには次の 7 つの重要な特性が必要です:
①有限性: アルゴリズムの有限性とは、アルゴリズムが限られた数のステップを実行した後に終了できなければならないことを意味します。
②明確性: アルゴリズムの各ステップには、正確な定義;
③入力: アルゴリズムには、操作オブジェクトの初期状況を記述するための 0 個以上の入力があります。
④ 出力: アルゴリズムには 1 つ以上の出力があります。入力データの処理結果を反映します。出力のないアルゴリズムは意味がありません。
⑤有効性: アルゴリズムで実行されるすべての計算ステップは、基本的な実行可能な操作ステップに分解できます。つまり、各計算ステップは時間内に有限数の完了で実行できます (有効性とも呼ばれます)。
⑥ 高効率: 高速実行と低リソース使用量。
⑦ 堅牢性: データに対する正しい応答。
2. 時間計算量
コンピューターサイエンスでは、アルゴリズムの時間計算量はアルゴリズムの実行時間を定量的に表す関数であり、時間計算量は一般に Big O 表記法 (Big O 表記法) で表されます。 Notation) は、関数の漸近的な動作を記述するために使用される数学的な表記法です。より正確には、別の (通常はより単純な) 関数に関して関数の大きさの漸近的な上限を記述するために使用されます。特に、漸近系列の残りの部分は、アルゴリズムの複雑さを分析するのに非常に役立ちます。この方法では、入力のサイズが漸近的であると言えます。値は無限大に近づきます。
ビッグオー、要するに「～の順番」という意味だと考えられます（おおよそ）。無限漸近
ビッグ O 記法は、アルゴリズムの効率を分析するときに非常に役立ちます。たとえば、サイズ n の問題を解くのにかかる時間 (または必要なステップ数) は、T(n) = 4n^2 - 2n + 2 で求められます。
n が増加すると、n^2; 項が優勢になり始め、他の項は無視できます。たとえば、n = 500 の場合、4n^2; 項は 2n 項よりも 1000 倍大きくなります。ほとんどの場合、後者を省略しても式の値に与える影響は無視できます。
2. 一般に、アルゴリズムの基本操作が繰り返される回数はモジュール n の関数 f(n) であるため、アルゴリズムの時間計算量は次のように記録されます。 f(n) ))。モジュール n が増加するにつれて、アルゴリズムの実行時間の増加率は f(n) の増加率に比例します。したがって、f(n) が小さいほど、アルゴリズムの時間計算量は低くなり、アルゴリズムの効率は高くなります。
3. 一般的な時間計算量
定数次数 O(1)、対数次数 O(log2n)、線形次数 O(n)、線形ペア次数は O(nlog2n)、二乗次数は O(n^2)、三次次数は O(n^3)、...、k 乗次数は O(n^k)、指数次数は次のようになります。 O(2^n)。
その中で、
1.O(n)、O(n^2)、3次次数O(n^3)、...、k次O(n^k)は多項式次数の時間計算量であり、それぞれ1次時間計算量、2次時間計算量と呼ばれます-注文時間の複雑さ。 。 。 。
2.O(2^n)、指数関数的な時間計算量、この種の時間計算量は現実的ではありません
3. 対数次数 O(log2n)、線形対数次数 O(nlog2n)、定数次数を除き、この種の効率は最高
例: アルゴリズム:
for（i=1;i<=n;++i）
{
for(j=1;j<=n;++j)
{
c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
for(k=1;k<=n;++k)
c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
}
} 次に、上記の括弧内の同じ桁数に従って、n^ を決定できます。 3 は T(n) と同じ桁です
次に、f(n) = n^3 となり、T(n)/f(n) に従って極限を見つけて定数 c を取得します
次に、時間アルゴリズムの複雑さ: T(n)=O(n^3)
IV. 定義: 問題のスケールが n の場合、アルゴリズムが問題を解くのに必要な時間は T(n)、これは n の関数です。T(n) はこのアルゴリズムを「時間計算量」と呼びます。
入力量 n が徐々に増加するとき、時間計算量の限界ケースは、アルゴリズムの「漸近時間計算量」と呼ばれます。
時間計算量を表すためにビッグ O 表記法がよく使用されますが、これは特定のアルゴリズムの時間計算量であることに注意してください。ビッグ O は上限があることを意味します。f(n)=O(n) の場合、明らかに上限が得られますが、そうではありません。最高ですが、人々は一般的に前者を表現することに慣れています。
さらに、問題自体にも複雑さがあり、特定のアルゴリズムの複雑さが問題の複雑さの下限に達した場合、そのようなアルゴリズムは最良のアルゴリズムと呼ばれます。
「ビッグ O 表記法」: この説明で使用される基本パラメーターは n です。これは問題インスタンスのサイズであり、複雑さまたは実行時間を n の関数として表します。ここでの「O」は順序を表します。たとえば、「二分探索は O(logn) です」、つまり「logn ステップでサイズ n の配列を取得する」必要があることを意味します。 n が増加すると、実行時間は最大でも f(n) に比例して増加します。
この漸近推定は、理論分析やアルゴリズムの大まかな比較には非常に価値がありますが、実際には詳細が違いを引き起こす可能性もあります。たとえば、小さい n に対しては、オーバーヘッドが低い O(n2) アルゴリズムの方が、オーバーヘッドが高い O(nlogn) アルゴリズムよりも高速に実行される可能性があります。もちろん、n が十分に大きくなると、関数の立ち上がりが遅いアルゴリズムはより高速に動作する必要があります。
O(1)
Temp=i;i=j;j=temp;定数。アルゴリズムの時間計算量は一定次数であり、T(n)=O(1) として記録されます。問題サイズ n の増加に伴ってアルゴリズムの実行時間が増加しない場合、アルゴリズムに数千のステートメントがある場合でも、その実行時間は大きな定数にすぎません。このタイプのアルゴリズムの時間計算量は O(1) です。
O(n^2)
2.1. iとjの内容を交換します
(1回) for(i=1;i1249bcee50fd9bd1458fe68ee4594939右サブツリー -> ルート ノード
例: 次のツリーの 3 つのトラバーサルを検索します
事前順序トラバーサル: abdefgc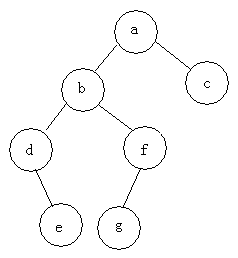
順序トラバーサル: debgfac
事後トラバーサル: edgfbca
タイプ二分木
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树
如何判断一棵树是完全二叉树？按照定义
教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。
首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。
一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。
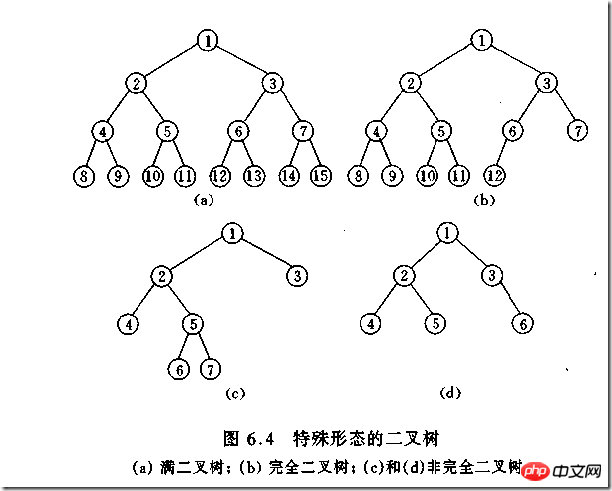
如何判断平衡二叉树？
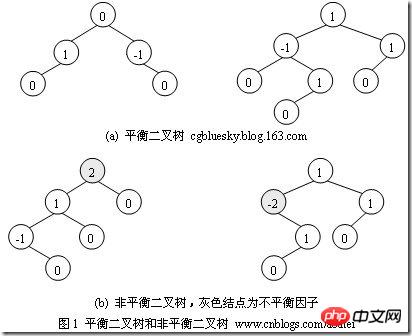
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1
（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1
二叉树遍历实现
class TreeNode(object):
def __init__(self,data=0,left=0,right=0):
self.data = data
self.left = left
self.right = right
class BTree(object):
def __init__(self,root=0):
self.root = root
def preOrder(self,treenode):
if treenode is 0:
return
print(treenode.data)
self.preOrder(treenode.left)
self.preOrder(treenode.right)
def inOrder(self,treenode):
if treenode is 0:
return
self.inOrder(treenode.left)
print(treenode.data)
self.inOrder(treenode.right)
def postOrder(self,treenode):
if treenode is 0:
return
self.postOrder(treenode.left)
self.postOrder(treenode.right)
print(treenode.data)
if __name__ == '__main__':
n1 = TreeNode(data=1)
n2 = TreeNode(2,n1,0)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5,n3,n4)
n6 = TreeNode(6,n2,n5)
n7 = TreeNode(7,n6,0)
n8 = TreeNode(8)
root = TreeNode('root',n7,n8)
bt = BTree(root)
print("preOrder".center(50,'-'))
print(bt.preOrder(bt.root))
print("inOrder".center(50,'-'))
print (bt.inOrder(bt.root))
print("postOrder".center(50,'-'))
print (bt.postOrder(bt.root))堆排序
堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
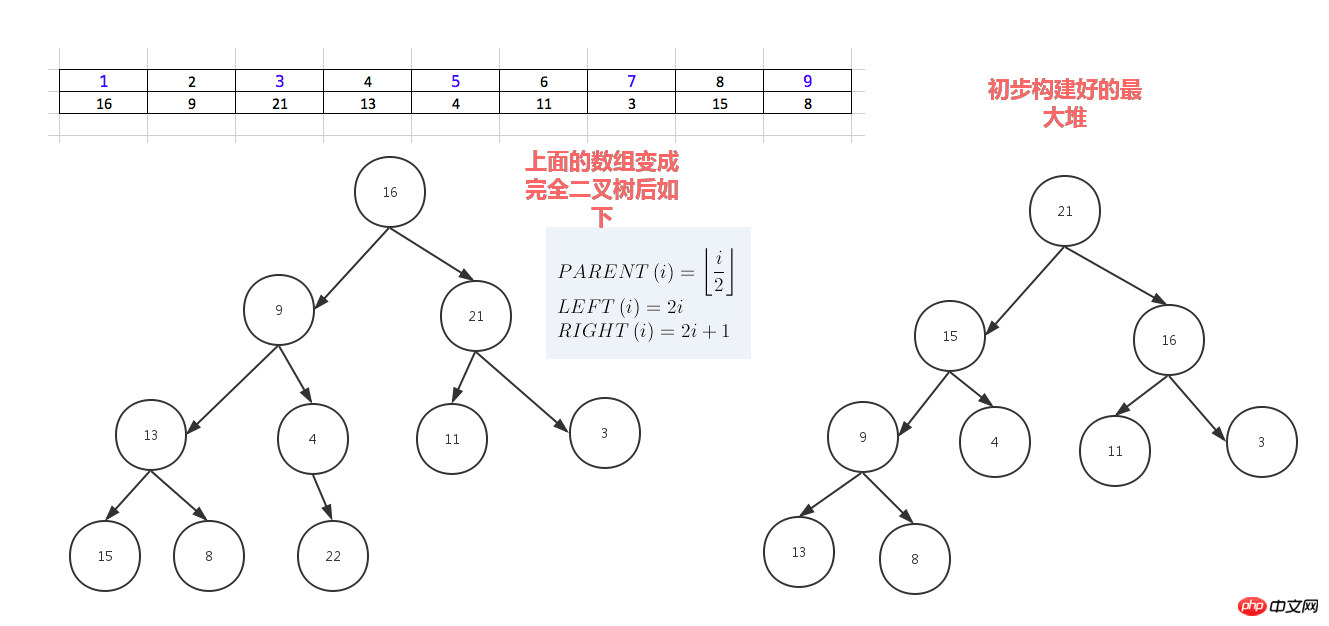
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。
堆排序就是把堆顶的最大数取出,
将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束
#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)
def main():
# [7, 95, 73, 65, 60, 77, 28, 62, 43]
# [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
#l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
#l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
array = [16,9,21,13,4,11,3,22,8,7,15,29]
#array = []
#for i in range(2,5000):
# #print(i)
# array.append(random.randrange(1,i))
print(array)
start_t = time.time()
heap_sort(array)
end_t = time.time()
print("cost:",end_t -start_t)
print(array)
#print(l)
#heap_sort(l)
#print(l)
if __name__ == "__main__":
main()人类能理解的版本
dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]
for i in range(len(dataset)-1,0,-1):
print("-------",dataset[0:i+1],len(dataset),i)
#for index in range(int(len(dataset)/2),0,-1):
for index in range(int((i+1)/2),0,-1):
print(index)
p_index = index
l_child_index = p_index *2 - 1
r_child_index = p_index *2
print("l index",l_child_index,'r index',r_child_index)
p_node = dataset[p_index-1]
left_child = dataset[l_child_index]
if p_node < left_child: # switch p_node with left child
dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
# redefine p_node after the switch ,need call this val below
p_node = dataset[p_index - 1]
if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
#if r_child_index < len(dataset[0:i]): #avoid right out of list index range
#print(left_child)
right_child = dataset[r_child_index]
print(p_index,p_node,left_child,right_child)
# if p_node < left_child: #switch p_node with left child
# dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
# # redefine p_node after the switch ,need call this val below
# p_node = dataset[p_index - 1]
#
if p_node < right_child: #swith p_node with right child
dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
# redefine p_node after the switch ,need call this val below
p_node = dataset[p_index - 1]
else:
print("p node [%s] has no right child" % p_node)
#最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆
print("switch i index", i, dataset[0], dataset[i] )
print("before switch",dataset[0:i+1])
dataset[0],dataset[i] = dataset[i],dataset[0]
print(dataset)希尔排序（shell sort）
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高
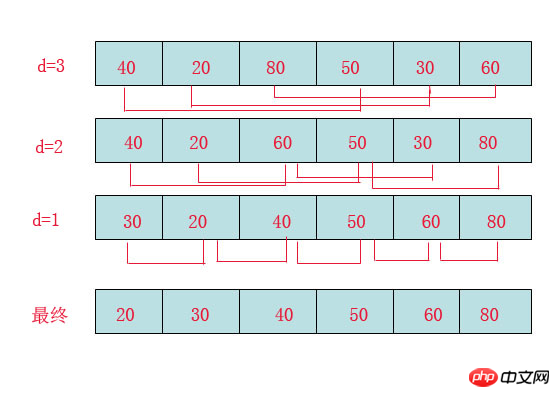
首先要明确一下增量的取法：
第一次增量的取法为： d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
看上图观测的现象为：
d=3时：将40跟50比，因50大，不交换。
将20跟30比，因30大，不交换。
将80跟60比，因60小，交换。
d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。
将20跟50比，不交换，继续将50跟80比，不交换。
d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。
希尔排序代码
import time,random
#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]
source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)
step = int(len(source)/2) #分组步长
t_start = time.time()
while step >0:
print("---step ---", step)
#对分组数据进行插入排序
for index in range(0,len(source)):
if index + step < len(source):
current_val = source[index] #先记下来每次大循环走到的第几个元素的值
if current_val > source[index+step]: #switch
source[index], source[index+step] = source[index+step], source[index]
step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
for index in range(1, len(source)):
current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
position = index
while position > 0 and source[
position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
source[position] = source[position - 1] # 把左边的一个元素往右移一位
position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
print(source)
t_end = time.time() - t_start
print("cost:",t_end)以上がPython で一般的に使用される基本的なアルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。