Javaのバイナリ演算とビット演算を詳しく解説

1. 表現方法:

Java 言語では、2 進数は 2 の補数を使用して表現され、最上位ビットは符号ビットであり、正の数の符号ビットは 0、負の数の符号ビットは 1 です。補完コードの表現は以下の要件を満たす必要があります。

(1) 正の数の最上位ビットは0で、残りのビットは値そのもの(2進数)を表します。

(2) 負の数の場合、その数値の絶対値の補数をビットごとに反転し、数値全体に 1 を加えます。

2.ビット演算子

ビット演算式は、整数型の2進数に対するビット演算を実装するオペランドとビット演算子で構成されます。ビット演算子は、論理演算子 (~、&、|、^ を含む) とシフト演算子 (>>、<<、>>> を含む) に分類できます。

1) 左シフト演算子 (<<) は、演算子の左側のオペランドを、演算子の右側で指定された桁数だけ左に移動できます (下位ビットに 0 を埋めます)。

2) 「符号付き」右シフト演算子 (>>) は、演算子の左側のオペランドを、演算子の右側で指定された桁数だけ右に移動します。 「符号付き」右シフト演算子は「符号拡張」を使用します。値が正の場合は上位ビットに 0 が挿入され、値が負の場合は上位ビットに 1 が挿入されます。

3) Java には、「符号なし」右シフト演算子 (>>>) も追加されました。これは、正か負かに関係なく、上位ビットに 0 を挿入する「ゼロ拡張」を使用します。この演算子は C または C++ では使用できません。

4) char、byte、または short がシフトされる場合、シフトが実行される前にそれらは自動的に int に変換されます。 右側の下位 5 ビットのみが使用されます。これにより、int 内で非現実的な桁数を移動することがなくなります。 Long 値が処理される場合、得られる最終結果も Long になります。このとき、long 値の既製桁数を超えないように、右側の下位 6 ビットのみが使用されます。 ただし、「符号なし」右シフトを実行するときに問題が発生する場合もあります。バイト値または short 値に対して右シフト演算を実行すると、結果が正しくない可能性があります (特に Java 1.0 および Java 1.1)。 これらは自動的に int 型に変換され、右にシフトされます。ただし、「ゼロ拡張」は起こらないため、そのような場合には -1 の結果が得られます。

バイナリは、コンピューティング技術で広く使用されている数値体系です。バイナリデータとは、0と1の2桁で表される数値です。その基数は 2、キャリー ルールは「2 対 1」、借用ルールは「1 を借りて 2 に等しい」です。これは 18 世紀のドイツの数学哲学の巨匠ライプニッツによって発見されました。現在のコンピュータシステムは基本的に２進法を採用しており、データは主に２の補数符号の形でコンピュータ内に格納される。コンピューターの 2 進法は非常に小さなスイッチであり、「オン」は 1 を表し、「オフ」は 0 を表します。

では、Java ではバイナリはどのように見えるのでしょうか?その神秘のベールを一緒に解き明かしましょう。

---

1. Java の組み込み基数変換

10 進数から 2 進数へ、および 2 進数から 10 進数へ変換する基本的な計算方法については、ここでは説明しません。

Java には、さまざまなベースの変換に役立つメソッドがいくつか組み込まれています。以下の図に示すように (整数整形を例として、他の型も同じです):

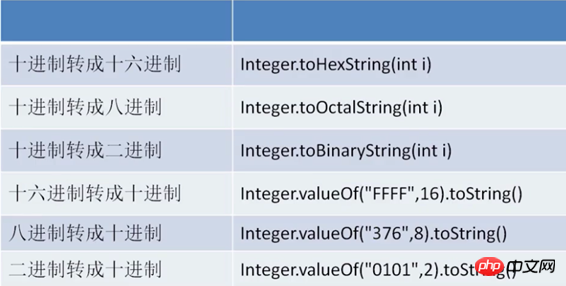
1、10 進数から他の基数に変換:

1 二进制：Integer.toHexString(int i);2 八进制：Integer.toOctalString(int i);3 十六进制：Integer.toBinaryString(int i);

2、他の基数から 10 進数に変換:

1 二进制：Integer.valueOf("0101",2).toString;2 八进制：Integer.valueOf("376",8).toString;3 十六进制：Integer.valueOf("FFFF",16).toString;

3, Integer クラスの parseInt() メソッドと valueOf() メソッドを使用して、他の基数を 10 進数に変換できます。

違いは、parseInt() メソッドの戻り値が int 型であるのに対し、valueOf() メソッドの戻り値は Integer オブジェクトであることです。

---

2. 基本的なビット演算

2進数は10進数と同じように加算、減算、乗算、除算ができますが、より単純な演算方法であるビット演算もあります。たとえば、コンピュータの int 型のサイズは 32 ビットであり、32 ビットの 2 進数で表現できるため、ビット演算を使用して int 型の値を計算できます。 もちろん、一部の計算には通常の方法を使用することもできます。ここでは主にビット演算の方法を紹介します。ビット演算には通常の演算方法とは比較にならない威力があることがわかります。 ビット演算のその他の応用については、次のブログ投稿「Magical Bit Operations」に移動してください。

まず、ビット演算の基本的な演算子を見てみましょう:

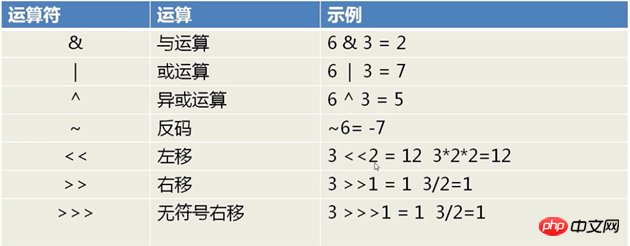
利点:

• 特定の状況 計算が簡単で高速で広くサポートされています

• 算術メソッドを使用すると、処理が遅く、ロジックが複雑になります

• ビット演算は1つの言語に限定されるものではなく、コンピューターの基本的な演算方法です

>>>>>>>>>>>> > >>>>>>>>>>>>>>>>>>>>>> > >>>>>>>>>> 0&1=0;

例: 51&5 は 0011 0011 & 0000 0101 =0000 0001 したがって、51&5=1.

特別な使い方

(1)クリア。

ユニットをゼロにクリアしたい場合は、バイナリ ビットがすべて 0 であっても、ビットがすべて 0 である値と AND 演算するだけで、結果は 0 になります。

(2)

数値内の指定された位置を取得します。

例: X=10101110 と仮定して、X の下 4 桁を取得し、X&0000 1111=0000 1110 を使用して取得します。

方法: x に取りたいビットに対応する数値を見つけます。その数値の対応するビットは 1 で、残りのビットは 0 です。この数値と x の AND 演算を実行して、x の指定されたビットを取得します。

(2) ビット単位の OR |

どちらか 1 つが 1 である限り、結果は 1 になります。

0|0=0; 1|0=1;

例: 51|5 は 0000 0101 =0011 0111 55

特別な使用法

は、データの特定の位置を するためによく使用されます。

方法: 1 に設定される x のビットに対応する数値を見つけます。数値の対応するビットは 1 で、残りのビットは 0 です。この数値は x に対する相対値であるか、x 内の特定の位置を 1 に設定します。

(3) XOR^

対応する 2 つのビットが「排他的」(異なる値) の場合、ビットの結果は 1 になり、そうでない場合は 0

0^0=0; 1^ 0=1; 1^1=0;

例: 51^5 は 0011 0011 ^ 0000 0101 =0011 0110 したがって、51^5=54

特別な使用法

(1) 排他的またはwith 1 ,

特定のビットを反転するには

方法: のビットに対応する数値を見つけます

例: X=1010 1110、下 4 桁を反転します。

(2) 0 との排他的論理和、元の値を保持

例:

C=A;A=B;B=C;

2. 加算と減算を使用して 2 つの変数の交換を実現します。

A=A+B;B=A-B;A=A-B;

3.ビットの使用 これは最も効率的な XOR 演算によって実現されます

原則: 数値の XOR 自体は 0 に等しい ^ B(4) 否定と演算~

は 2 進数をビット単位で反転します。つまり、0 を 1 に、1 を 0 に変更します

~1=0; ~0=1

(5) 左シフト< <

オペランドのすべてのバイナリ ビットを特定のビット数だけ左にシフトします (左側のバイナリ ビットは破棄され、右側に 0 が追加されます)

例: 2<<1 =4 10<<1=100 左にシフトするときに破棄される上位ビットに 1 が含まれていない場合、左にシフトされる各ビットは数値を 2 で乗算することと同じになります。

例:

11(1011)<<2= 0010 1100=22

11(00000000 00000000 00000000 1011) 32 ビットのシェーピング

(6) 右シフト>>

数値のすべての 2 進数を特定のビット数だけ右にシフトし、正の数の場合は左に 0 を追加し、負の数の場合は 1 を追加し、右側を破棄します。 右シフト時の丸め上位ビットが 1 ではない (つまり、負の数ではない) 場合、オペランドが右にシフトされるたびに、数値を 2 で割ることと同じになります。

左側に 0 を埋め込むか 1 を埋め込むかは、移動する数値が正か負かによって決まります。

例: 4>>2=4/2/2=1

-14 (つまり 1111 0010)>>2 =1111 1100=-4

(7) 符号なし右シフト演算> ;>

各ビットは指定された桁数だけ右にシフトされます。 が右にシフトされた後、左側の空のビットは 0 で埋められます、右側のビットは削除されて破棄されます。

例: -14>>>2

(つまり、11111111 11111111 11111111 11110010)>2

=(001111 11 11 111111 11111111 11111100)=1073741820

>>>>>>>>>>>>>>>>>>>>>>>>> ;> ;>>>>>>>>>>>>>>>>>>>>>>>> ;> ;>>>

上記の負の数の 2 進数のビット表現は、正の数の場合とは若干異なるため、ビット単位の演算も正の数とは異なります。

負の数は正の数の補数形式で表現されます!

上記の-14を例に、元のコード、逆コード、補コードを簡単に説明します。

元のコード

整数を絶対値に従って2進数に変換したものを元のコードといいます

例: 00000000 00000000 00000000 00001110は14の元のコードです。

逆コード

2 進数をビットごとに反転し、その結果得られる新しい 2 進数は、元の 2 進数の 1 の補数と呼ばれます。

例: 00000000 00000000 00000000 00001110,

の各ビットを否定します 11111111 11111111 11111111 11110001

注: これら 2 つは相互に補完するものです

補数に1を加えたものを補数といいます

11111111 11111111 11111111 11110001 +1=

11111111 11111111 11111111 111100 10

これで、-14 のバイナリ表現が得られました。それを左にシフトします

?

分析: この 2 進数の最初のビットは 1 であり、2 の補数の形式であることを示しています。次に、補数を元のコード (正の値) に変換する必要があります。

元のコードの変換の逆です。コード手順:

補数から 1 を引いて逆コードを取得します: (11000111) 最初の 24 ビットは 1 ですが、ここでは省略します

逆コードは次のように反転されます。元のコード (つまり、負の数の正の値) を取得します (00111000)

1. 正の値を計算します、正の値は 56 です

2. 正の値の反対の数を取り、結果を取得します-56

3. 結論: -14
3. Java システム運用の進歩

4. Java ではバイナリがよく使われますか?

通常の開発では「基数変換」や「ビット演算」はあまり使われず、高度なタスクはJavaが処理します。

ファイルの読み書き、データ通信など、クロスプラットフォームでよく使用されます。

---

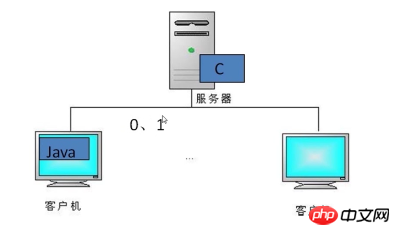
シナリオを見てみましょう:

クライアントとサーバーの両方が Java 言語で書かれたプログラムである場合、クライアントがオブジェクト データを送信するときに、送信されるデータをシリアル化可能にシリアル化し、サーバーはシーケンス 変換されたデータをデシリアライズして、内部のオブジェクト データを読み出すことができます。

クライアントのアクセス数が増えると、サーバーのパフォーマンスは考慮されなくなります。実際、実現可能な解決策は、サーバーの Java 言語を C 言語に変更することです。

C言語はJava言語よりも応答速度が速いので、このときクライアントがシリアル化されたデータを渡すと、サーバー側のC言語は解析できなくなります。サーバーがこれらの言語を解析できるように、データをバイナリ (0,1) に変換できます。

>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>

Java には 4 つの基本的な

データ型があります:

1. Int データ型: byte (8 ビット、-128~127)、short (16 ビット) )、int (32bit)、long (64bit)

2. float データ型: 単精度 (float、32bit)、倍精度 (double、64bit)

3. Boolean 型変数には true 値と false 値があります (両方とも 1bit) )

4. char データ型: Unicode 文字、16 ビット

対応するクラス型:

Integer、Float、Boolean、Character、Double、Short、Byte、Long

>> ;>> >>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>

(1) データ型を byte に変換します

例: int type 8143 (00000000 00000000 00011111 11001111)

=>byte[] b=[-49,31,0,0 ]

First (下位) バイト: 8143>>0*8 & 0xff=(11001111)=207 (または符号付き -49)

2 番目 (下位) バイト: 8143>>0*8 &0xff=(00011111)= 31

3 番目 (下位) バイト: 8143>>2*8 &0xff=00000000=0

4 番目 (下位) バイト: 8143>> ;3*8 &0xff=00000000=0

上記 (ローエンド) は右から左に始まることに気付きましたが、ローエンドは何でしょうか?ビッグエンディアンとスモールエンディアンの観点から説明しましょう。

リトルエンディアン方式 (Little-Endian)

下位ビットバイトは、値の開始アドレスであるメモリの下位アドレスの端に配置され、上位ビットバイトアドレス側

ビッグエンディアン)

上位

バイトがメモリ内に配置されます。下位アドレス側は値の開始アドレスであり、 lowバイトはメモリ内に配置されますhighアドレスは終了

なぜビッグエンディアンモードとスモールエンディアンモードがあるのですか?

これは、コンピューター システムでは、各アドレス単位が 1 バイトに対応し、1 バイトが 8 ビットであるためです。しかし、C

言語では、8ビットのcharに加えて、16ビットのshort型と32ビットのlong型も存在します(特定のコンパイラに応じて)さらに、8を超えるプロセッサの場合。 16 ビットや 32 ビットのプロセッサでは、レジスタ幅が 1 バイトよりも大きいため、複数のバイトを配置するという問題が発生するはずです。これは、ビッグエンディアン ストレージ モードとリトル エンディアン ストレージ モードにつながります。たとえば、16 ビットの short 型 x のメモリ内のアドレスは 0x0010 で、x の値は 0x1122 になります。この場合、0x11 が上位バイト、0x22 が下位バイトになります。ビッグエンディアン モードの場合、下位アドレス (0x0010) に 0x11 を、上位アドレス (0x0011) に 0x22 を入力します。リトルエンディアンモードはその逆です。一般的に使用される X86 構造はリトル エンディアン モードですが、KEIL C51 はビッグ エンディアン モードです。多くの ARM および DSP はリトルエンディアン モードです。一部の ARM プロセッサでは、ハードウェアによってビッグ エンディアン モードまたはリトル エンディアン モードを選択することもできます。 例: 32 ビット数値 0x12 34 56 78 (16 進数)

ビッグエンディアン モード CPU (アドレス 0x4000 から始まると仮定) の記憶方法は、

メモリ アドレス

0x4000	0x4001	0x4002	0x4003
存放内容	0x78	0x56	0x34	0x12

在Little-Endian模式CPU的存放方式（假设从地址0x4000开始存放）为

内存地址	0x4000	0x4001	0x4002	0x4003
存放内容	0x12	0x34	0x56	0x78

 （二）字符串转化为字节

1.字符串->字节数组

1 String s;2 byte[] bs=s.getBytes();

2.字节数组->字符串

1 Byte[] bs=new byte[int];2 String s =new String(bs);或3 String s=new String(bs,encode);//encode指编码方式，如utf-8

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

两种类型转化为字节的方法都介绍了，下面写个小例子检验一下：

 1 public class BtyeTest { 2     /* 3      * int整型转为byte字节 4      */ 5     public static byte[] intTOBtyes(int in){ 6         byte[] arr=new byte[4]; 7         for(int i=0;i<4;i++){ 8             arr[i]=(byte)((in>>8*i) & 0xff); 9         }10         return arr;11     }12     /*13      * byte字节转为int整型14      */15     public static int bytesToInt(byte[] arr){16         int sum=0;17         for(int i=0;i<arr.length;i++){18             sum+=(int)(arr[i]&0xff)<<8*i;19         }20         return sum;21     }22     public static void main(String[] args) {23         // TODO Auto-generated method stub24         byte[] arr=intTOBtyes(8143);25         for(byte b:arr){26             System.out.print(b+" ");27         }28         System.out.println();29         System.out.println(bytesToInt(arr));30         31         //字符串与字节数组32         String str="云开的立夏de博客园";33         byte[] barr=str.getBytes();34         35         String str2=new String(barr);36         System.out.println("字符串转为字节数组：");37         for(byte b:barr){38             System.out.print(b+" ");39 40         }41         System.out.println();42 43         System.out.println("字节数组换位字符串："+str2);44         45          46     }47 48 }

运行结果：

---

结束语：最近偷懒了，没有好好学习，好几天没写文了，哎，还请大家多多监督！

以上がJavaのバイナリ演算とビット演算を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。