ホームページ >バックエンド開発 >Python チュートリアル >Python でよく使用される並べ替えの例を共有する
Python でよく使用される並べ替えの例を共有する
- PHP中文网オリジナル
- 2017-06-21 16:40:361425ブラウズ
ソートアルゴリズムの安定性と重要性
バブルソート
複雑さと安定性
選択ソート
挿入ソート
ヒルソート
-
クイックソート
一般的なソートアルゴリズムの効率の比較
ソートアルゴリズムの安定性と重要性
ソート対象のシーケンス内に、同じキーワードを持つレコードがあり、ソート後もこれらのレコードの相対的な順序は変化しません。ソートアルゴリズムは安定しています。
並べ替えが不安定なので、複数のキーワードの並べ替えを完了できません。たとえば、整数の並べ替えでは、桁数が多いほど優先順位が高く、上位の桁から下位の桁へ並べ替えられます。したがって、各ビットのソートには安定したアルゴリズムが必要であり、そうでないと正しい結果が得られません。
つまり、 複数のキーワードを複数回ソートしたい場合は、安定したアルゴリズムを使用する必要があります
バブルソート
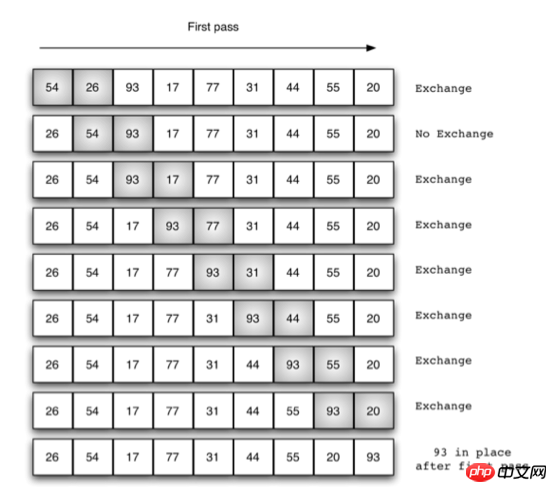 

def bubble_sort(alist):
"""
冒泡排序
"""
if len(alist) <= 1:
return alist
for j in range(len(alist)-1,0,-1):
for i in range(j):
if alist[i] > alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
return alist
複雑さと安定性
最適な時間計算量: ( O(n) ) 走査では交換できる要素が見つからず、ソートが終了します
最悪の時間計算量: (O(n^2))
安定性: 安定しています
選択ソート
選択ソートはシンプルで直感的な並べ替えアルゴリズム。仕組みは次のとおりです。まず、ソートされていないシーケンス内で最小の (大きい) 要素を見つけて、ソートされたシーケンスの先頭に格納します。次に、ソートされていない残りの要素から最小の (大きい) 要素を見つけて、それをソートされたシーケンスの最後に置きます。ソートされたシーケンス。すべての要素がソートされるまで続きます。
挿入ソート
挿入ソートは、並べ替えられていないデータの場合、並べ替えられたシーケンスの後ろから前に向かってスキャンして、対応する位置を見つけて挿入します。挿入ソートの実装では、後ろから前へのスキャン プロセス中に、最新の要素に挿入スペースを提供するために、ソートされた要素を繰り返し徐々に後方に移動する必要があります。
 

def insert_sort(alist):
"""
插入排序
"""
n = len(alist)
if n <= 1:
return alist
# 从第二个位置,即下表为1的元素开始向前插入
for i in range(1, n):
j = i
# 向前向前比较,如果小于前一个元素,交换两个元素
while alist[j] < alist[j-1] and j > 0:
alist[j], alist[j-1] = alist[j-1], alist[j]
j-=1
return alist
複雑さと安定性
最適な時間計算量: O((n)) (昇順に並べられており、シーケンスはすでに昇順になっています)
最悪の時間計算量: O( (n ^2))
安定性: 安定
ヒルソート
ヒルソート(シェルソート)は挿入ソートを改良したものであり、ソートは安定していません。ヒルソートでは、添字の特定の増分でレコードをグループ化し、直接挿入ソートアルゴリズムを使用して各グループをソートします。増分が徐々に減少するにつれて、各グループにはさらに多くのキーワードが含まれます。今度は、ファイル全体が 1 つのグループに分割され、アルゴリズムが終了します。
def shell_sort(alist): n = len(alist) gap = n//2 # gap 变化到0之前,插入算法之行的次数 while gap > 0: # 希尔排序, 与普通的插入算法的区别就是gap步长 for i in range(gap,n): j = i while alist[j] < alist[j-gap] and j > 0: alist[j], alist[j-gap] = alist[j-gap], alist[j] j-=gap gap = gap//2 return alist
複雑さと安定性
最適な時間計算量: (O(n^{1.3})) (注文する必要はありません)
最悪の時間計算量: (O(n^) 2))
安定性: 不安定
クイックソート
クイックソート(クイックソート)は、一度のソートでソート対象のデータを2つの独立した部分に分割し、一方の部分のすべてのデータが他方の部分よりも優れている必要があります。次に、このメソッドを使用してデータの 2 つの部分をそれぞれすばやく並べ替えます。並べ替えプロセス全体を再帰的に実行できるため、データ全体が順序付けされたシーケンスになります。
手順は次のとおりです:
シーケンスから「ピボット」と呼ばれる要素を選択します
シーケンスを並べ替えます。ピボット値より小さいすべての要素がピボットの前に配置され、ピボット値より小さいすべての要素が配置されます。ピボット値はピボットの前に配置されます。より大きな値を持つ値はベースの後ろに配置されます (同じ数値をどちらの側にも置くことができます)。この分割の後、データはシーケンスの途中にあります。これをパーティション操作と呼びます。
基本値より小さい要素の部分配列と基本値より大きい要素の部分配列を再帰的に並べ替えます。
再帰の最も低いケースは、配列のサイズが 0 または 1 の場合、つまり、配列が常にソートされている場合です。再帰は続けられますが、各反復 (反復) で少なくとも 1 つの要素が最終位置に移動するため、このアルゴリズムは常に終了します。
一般的な並べ替えアルゴリズムの効率の比較
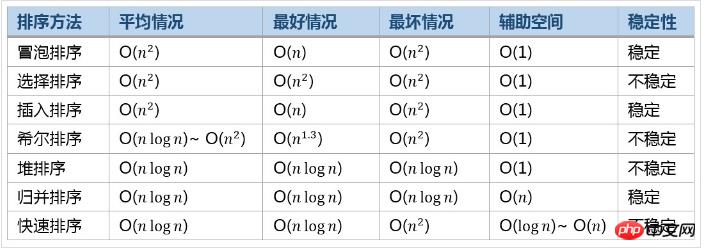 

以上がPython でよく使用される並べ替えの例を共有するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

