深さ優先アルゴリズムと幅優先アルゴリズムの例の詳細な説明

まず最初に、ここで Algorithms ウェブサイトの 2 番目の部分を紹介しましょう。これは、書籍 Algorithms のオンライン コースです。

さらに、Coursera のグラフ アルゴリズムに関するコースも非常に優れています。

グラフを表現するいくつかの方法:

その方法 (データ構造) を使用してグラフを表現するには、次の 2 つの要件が含まれます: (1) スペースが適切である必要があります (2)インスタンスのメソッド 実装は高速である必要があります

次に、3 つのオプションがあります:

(1) 次のようなエッジのセット:

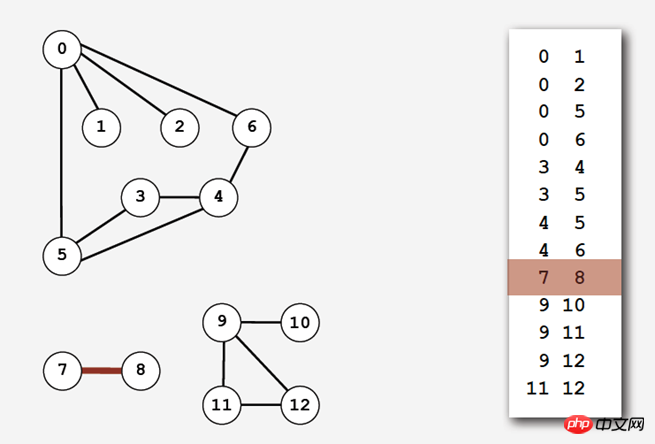
シンプルですが 2 番目の条件を満たしていません条件 - 隣接関係を達成するためのテーブル adj() は、グラフ内のすべてのエッジを走査します。

(2) 隣接行列:

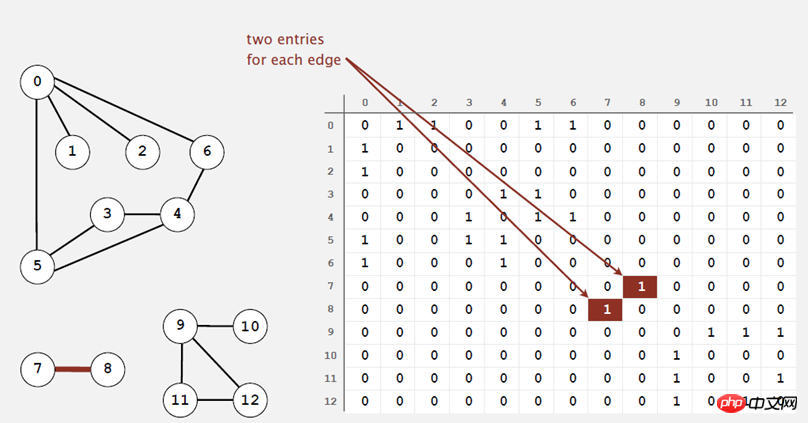
V 倍の V を使用すると、空間ではブール証明が満たされません。

(3) 隣接リスト:

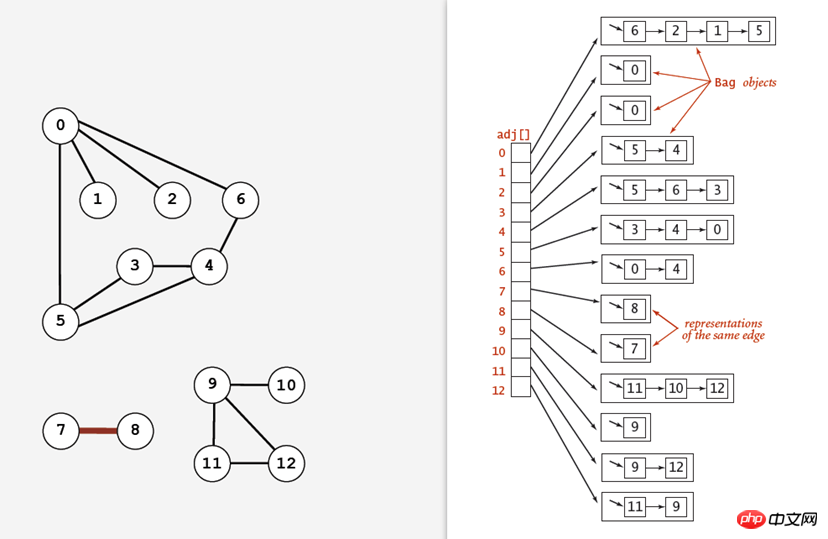
は、頂点をインデックスとして持つ配列リストを使用し、その中の各要素は頂点に隣接する頂点のリストです。

上記の方法は柔軟性が高いため、隣接リストで表現する場合、次のようなデータ構造を定義して Graph オブジェクトを表現できます。

public class Graph
{private readonly int verticals;//顶点个数private int edges;//边的个数private List<int>[] adjacency;//顶点联接列表public Graph(int vertical)
    {this.verticals = vertical;this.edges = 0;
        adjacency=new List<int>[vertical];for (int v = 0; v < vertical; v++)
        {
            adjacency[v]=new List<int>();
        }
    }public int GetVerticals ()
    {return verticals;
    }public int GetEdges()
    {return edges;
    }public void AddEdge(int verticalStart, int verticalEnd)
    {
        adjacency[verticalStart].Add(verticalEnd);
        adjacency[verticalEnd].Add(verticalStart);
        edges++;
    }public List<int> GetAdjacency(int vetical)
    {return adjacency[vetical];
    }
}

深さ優先アルゴリズム

深さ優先アルゴリズムについて話す前に、まず迷路探索問題について見てみましょう。迷路とグラフの対応は次のとおりです:

迷路の各交点はグラフの頂点を表し、各チャネルはエッジに対応します。

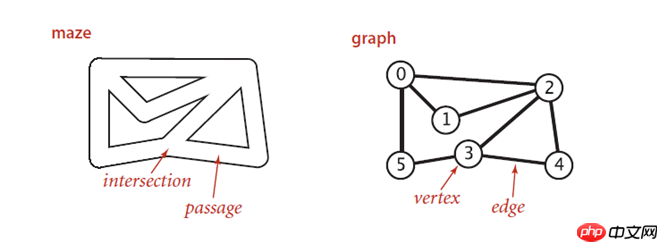
トレモーロープ探索法を使用して迷路を探索できます。つまり:

• 後ろにロープを張ります

• 訪れるすべての場所にロープを張り、集合場所と訪問する通路をマークします

• すでに訪れた場合は、ロープに沿ってまだ訪れていない場所に戻ります:

イラストは次のとおりです:

以下は迷路探索の小さなアニメーションです:

深さ優先探索アルゴリズムは迷路探索をシミュレートします。実際のグラフ処理アルゴリズムでは、通常、グラフの表現とグラフの処理ロジックを分離します。したがって、アルゴリズムの全体的な設計パターンは次のとおりです。

• Graph オブジェクトを作成します

• Graph オブジェクトを Paths オブジェクトなどのグラフ アルゴリズム処理オブジェクトに渡します

• 次に、処理された結果をクエリします。情報

を取得するために、dfs メソッドが再帰的に呼び出され、 が Marked[] マーク配列を維持し、 を呼び出す前にノードが訪問されたかどうかを判断することがわかります。

深さ優先アルゴリズムの説明: 頂点を訪問するとき

1. マークされていない隣接する頂点をすべて再帰的に訪問します。

りー

试验一个算法最简单的办法是找一个简单的例子来实现。

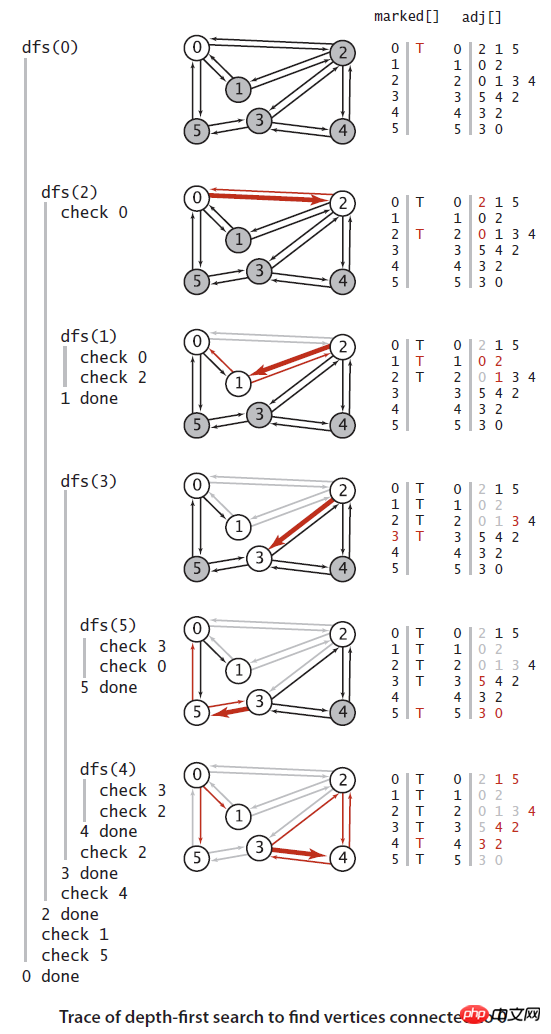
算法应用：

连通性。给定一幅图，回答“两个给定顶点是否连通？” 或者 “图中有多少个连通子图？”

寻找路径。给定一幅图和一个起点，回答“从s到给定目的顶点v是否存在一条路径？如果有，找出这条路径。”

检测环。给定的图是无环图吗？

双色问题。能够用两种颜色将图的所有顶点着色，使得任意一条边连个顶点的颜色都不相同？这个问题等价于：这是一个二分图吗？

 

深度优先路径查询

有了这个基础，我们可以实现基于深度优先的路径查询，要实现路径查询，我们必须定义一个变量来记录所探索到的路径。

所以在上面的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录，和仅记录从当前节点到起始节点不同，我们记录图中的每一个节点到开始节点的路径。为了完成这一日任务，通过设置edgesTo[w]=v，我们记录从v到w的边，换句话说，v-w是做后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。

注意代码只是在前面算法的基础上维护了一个edgTo数组，并用栈Stack保存路径。

public class DepthFirstPaths
{private bool[] marked;//记录是否被dfs访问过
    private int[] edgesTo;//记录最后一个到当前节点的顶点private int s;//搜索的起始点public DepthFirstPaths(Graph g, int s)
    {
        marked = new bool[g.GetVerticals()];
        edgesTo = new int[g.GetVerticals()];this.s = s;
        dfs(g, s);
    }private void dfs(Graph g, int v)
    {
        marked[v] = true;foreach (int w in g.GetAdjacency(v))
        {if (!marked[w])
            {                edgesTo[w] = v;dfs(g,w);
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v){if (!HasPathTo(v)) return null;
        Stack<int> path = new Stack<int>();for (int x = v; x!=s; x=edgesTo[x])
        {
            path.Push(x);
        }
        path.Push(s);return path;
    }
}

 

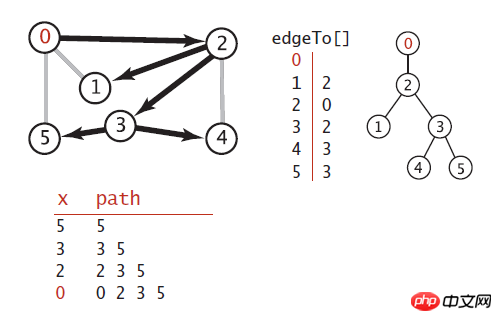
上图中是黑色线条表示 深度优先搜索中，所有定点到原点0的路径， 他是通过edgeTo[]这个变量记录的，可以从右边可以看出，

他其实是一颗树，树根即是原点，每个子节点到树根的路径即是从原点到该子节点的路径。

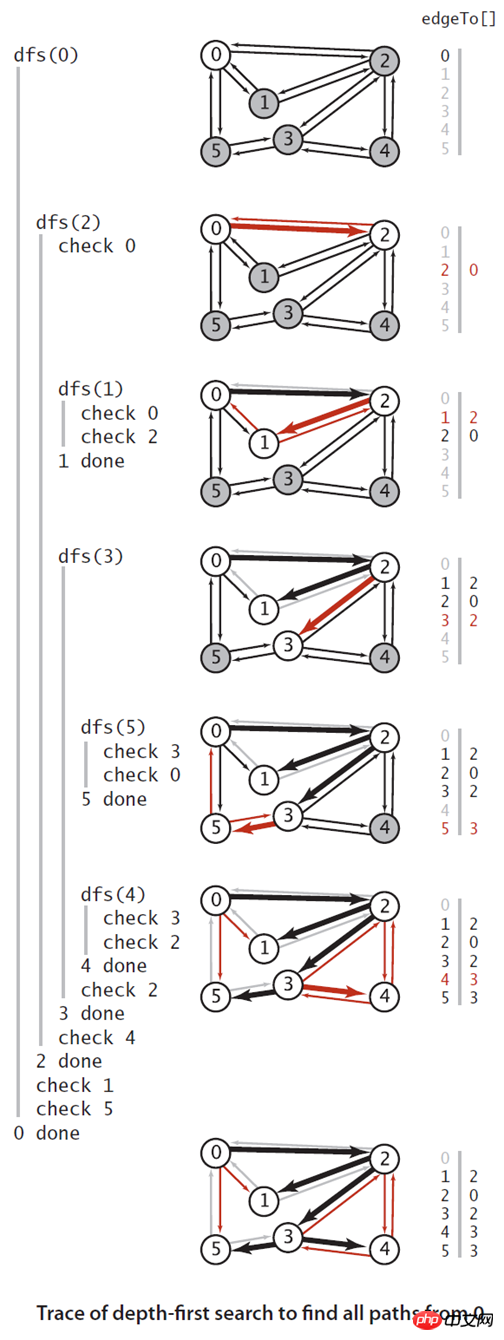
下图是深度优先搜索算法的一个简单例子的追踪。

 

 

 

连通分量

API如下：

CC的实现使用了marked[ ]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。递归的深搜第一次调用的参数是顶点0，会标记所有与0连通的顶点。然后构造函数中的for循环会查找每个没有被标记的顶点并递归调用dfs来标记和它相邻的所有顶点。另外，它还使用了一个以顶点作为索引的数组id[ ],将同一个连通分量中的顶点和连通分量的标识符关联起来。这个数组使得connected( )方法的实现变得十分简单。

public class CC {private boolean[] marked;private int[] id;private int count;public CC(Graph g){
        marked = new boolean[g.getVertexCount()];
        id = new int[g.getVertexCount()];for(int s = 0; s < g.getVertexCount(); s++){if(!marked[s]){
                dfs(g,s);
                count++;
            }
        }
    }private void dfs(Graph g, int v) {
        marked[v] = true;
        id[v] = count;for(int w: g.adj(v))if(!marked[w])
                dfs(g,w);
    }/** v和w连通吗*/public boolean connected(int v, int w)    { return id[v] == id[w]; }/** v所在的连通分量的标识符*/public int id(int v)    { return id[v]; }/** 连通分量数*/public int count()        {return count;}

 

检测环

/**
 * 给定的图是无环图吗
 * 检测自环:假设没有自环，没有平行边 */public class Cycle {private boolean[] marked;private boolean hasCycle;public Cycle(Graph g){
        marked = new boolean[g.getVertexCount()];for(int i = 0;i<g.getVertexCount();i++)if(!marked[i])    dfs(g, i, i);
    }private void dfs(Graph g, int v, int u) {
        marked[v] = true;for(int w: g.adj(v))if(!marked[w])    dfs(g, w, v); // 若w没被标记过，那么从w继续递归深搜，把w的父节点作为第二参数else if(w != u) hasCycle = true; // 若w被标记过，那么若无环，w必然和父节点相同，否则就是有环    }/** 是否含有环*/public boolean hasCycle(){return hasCycle;}

 

双色问题

/**
 * 双色问题：能够用两种颜色将图的所有顶点着色，使得任意一条边上的两个端点的颜色都不同吗？
 * 等价于：判断是否是二分图的问题 */public class TwoColor {private boolean[] marked;private boolean[] color;private boolean isColorable;public TwoColor(Graph g){
        isColorable = true;
        marked = new boolean[g.getVertexCount()];
        color = new boolean[g.getVertexCount()];for(int i = 0; i<g.getVertexCount(); i++)//遍历所有顶点if(!marked[i])    dfs(g, i);//没有mark就进行深搜    }private void dfs(Graph g, int v) {
        marked[v] = true;        // 标记for(int w: g.adj(v))    // 对邻接表进行遍历if(!marked[w]){        // 如果没有被标记color[w] = !color[v];    // 当前w节点颜色置为和父节点不同的颜色dfs(g, w);                // 对当前节点继续深搜}else if(color[w] == color[v]){    // 如果已经被标记，看是否颜色和父节点相同isColorable = false;         // 若相同则不是二分图            }
    }/** 是否是二分图*/public boolean isBipartite(){return isColorable;}

 

 

广度优先算法

通常我们更关注的是一类单源最短路径的问题，那就是给定一个图和一个源S，是否存在一条从s到给定定点v的路径，如果存在，找出最短的那条(这里最短定义为边的条数最小)

深度优先算法是将未被访问的节点放到一个堆中(stack)，虽然在上面的代码中没有明确在代码中写stack，但是 递归间接的利用递归堆实现了这一原理。

和深度优先算法不同， 广度优先是将所有未被访问的节点放到了队列中。其主要原理是：

先将起点加入队列，然后重复一下步骤直到队列为空：

1.取队列中的下一个顶点V并标记它

2.将与v相邻的所有未被标记过的顶点加入队列

广度优先是以距离递增的方式来搜索路径的。

class BreadthFirstSearch
{private bool[] marked;private int[] edgeTo;private int sourceVetical;//Source verticalpublic BreadthFirstSearch(Graph g, int s)
    {
        marked=new bool[g.GetVerticals()];
        edgeTo=new int[g.GetVerticals()];this.sourceVetical = s;
        bfs(g, s);
    }private void bfs(Graph g, int s)
    {
        Queue<int> queue = new Queue<int>();
        marked[s] = true;
        queue.Enqueue(s);while (queue.Count()!=0)
        {int v = queue.Dequeue();foreach (int w in g.GetAdjacency(v))
            {if (!marked[w])
                {
                    edgeTo[w] = v;
                    marked[w] = true;
                    queue.Enqueue(w);
                }
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v)
    {if (!HasPathTo(v)) return null;

        Stack<int> path = new Stack<int>();for (int x = v; x!=sourceVetical; x=edgeTo[x])
        {
            path.Push(x);
        }
        path.Push(sourceVetical);return path;
    }

}

算法应用：最短路径问题

 

总结：

深度优先搜索和广度优先搜索都是将起点存入数据结构中，然后重复一下步骤直到数据结构被清空：

1.取其中的下一个顶点并标记它

2.将v的所有相邻而未被标记的顶点加入数据结构

这两个算法 的不同之处仅在于从数据结构中获取下一个顶点的规则（广度优先来说是最早加入的顶点，对于深度优先搜索来说是最晚加入的顶点）。

 

以上が深さ優先アルゴリズムと幅優先アルゴリズムの例の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。