ホームページ >Java >＆＃＆チュートリアル >Java の赤黒ツリー実装の詳細な分析 (写真)
Java の赤黒ツリー実装の詳細な分析 (写真)
- 黄舟オリジナル
- 2017-03-20 10:37:361660ブラウズ
赤黒ツリーは、平衡二分探索ツリーの一種です。赤黒ツリーを深く理解するには、二分探索ツリーから始める必要があります。
Java の赤黒ツリー実装の詳細な分析 (写真)
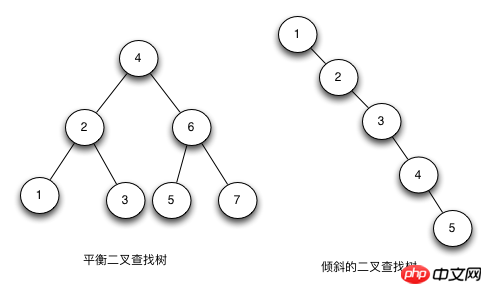
二分探索木 (Java の赤黒ツリー実装の詳細な分析 (写真)) は、左側の子ノードの値が親ノードの値より小さく、右側のノードの値が親ノードの値より大きいです。その高さによって検索効率が決まります。
理想的な状況では、二分探索木の追加、削除、変更の時間計算量は O(logN) (N はノード数) で、最悪の場合は O(N) になります。その高さが logN+1 であるとき、二分探索木はバランスがとれていると言います。
Java の赤黒ツリー実装の詳細な分析 (写真)検索操作
T key = a search key
Node root = point to the root of a Java の赤黒ツリー実装の詳細な分析 (写真)
while(true){
if(root==null){
break;
}
if(root.value.equals(key)){
return root;
}
else if(key.compareTo(root.value)<0){
root = root.left;
}
else{
root = root.right;
}
}
return null;プログラムからわかるように、Java の赤黒ツリー実装の詳細な分析 (写真)が検索されると、まず現在のノードと比較されます:
等しい場合は、現在のノードを返します。 less 現在のノードより大きい場合は、現在のノードの左側のノードの検索を続けます。
現在のノードより大きい場合は、現在のノードの右側のノードの検索を続けます。
現在のノードポインタが空になるか、対応するノードが見つかるまで、プログラムの検索は終了します。
Java の赤黒ツリー実装の詳細な分析 (写真)挿入操作
Node node = create a new node with specify value
Node root = point the root node of a Java の赤黒ツリー実装の詳細な分析 (写真)
Node parent = null;
//find the parent node to append the new node
while(true){
if(root==null)break;
parent = root;
if(node.value.compareTo(root.value)<=0){
root = root.left;
}else{
root = root.right;
}
}
if(parent!=null){
if(node.value.compareTo(parent.value)<=0){//append to left
parent.left = node;
}else{//append to right
parent.right = node;
}
}挿入操作は、まずループを通じて挿入されるノードの親ノードを見つけます。親ノードを見つけるロジックは同じで、小さい方が左に進み、大きい方が左に進みます。権利。親ノードを見つけたら、親ノードを比較し、小さい方を親ノードの左側のノードに挿入し、大きい方を親ノードの右側のノードに挿入します。
Java の赤黒ツリー実装の詳細な分析 (写真)の削除操作
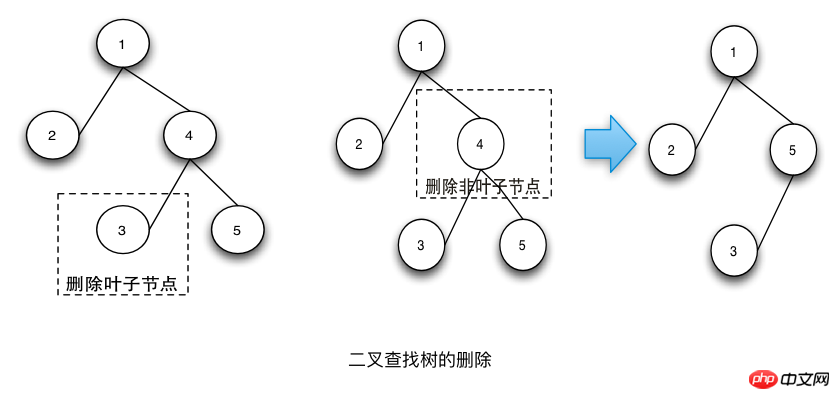
削除操作の手順は次のとおりです:
削除するノードを見つけます。
削除対象のノードがリーフノードの場合は、直接削除します。
削除するノードがリーフノードではない場合、まず削除するノードの順序トラバーサルの後続ノードを見つけ、削除するノードの値を後続ノードの値に置き換えますを選択し、後続ノードを削除します。
Java の赤黒ツリー実装の詳細な分析 (写真) の主な問題は、数値を挿入するとツリーが傾いてしまうことです。挿入オーダーが異なると、ツリーの高さも異なります。ツリー検索の効率に直接影響します。理想的な高さは logN です。最悪の場合は、すべてのノードが対角線上にあり、そのようなツリーの高さは N です。
RBTree
Java の赤黒ツリー実装の詳細な分析 (写真)の既存の問題に基づいて、新しいツリーであるBalanced Binary Search Tree (Balanced Java の赤黒ツリー実装の詳細な分析 (写真))が作成されました。挿入および削除する場合、バランスの取れたツリーは回転操作を通じて logN の高さを維持します。代表的な 2 つのバランス ツリーは、AVL ツリーと赤黒ツリーです。 AVL ツリーは実装が複雑で、挿入と削除のパフォーマンスが低いため、実際の環境でのアプリケーションは赤黒ツリーほど良くありません。
Red-Black Tree (以下、RBTree) は、Linux カーネルの完全に公平なスケジューラ、高精度タイマー、ext3 ファイルシステムなど、およびさまざまな言語の関数ライブラリなど、幅広い実用的なアプリケーションを備えています。 Java TreeMap および TreeSet、C++ STL マップ、マルチマップ、マルチセットなど。
RBTree は、関数型言語で最も一般的に使用される永続データ構造の 1 つであり、計算幾何学でも重要な役割を果たします。 Java 8 での HashMap 実装のパフォーマンスは、リンク リストを RBTree に置き換えることによって改善されたことに言及する価値があります。
RBTreeの定義
RBTreeは次のように定義されます:
どのノードにも黒または赤の色があります
ルートノードは黒です
親ノードと子ノードの間に2つの連続する赤は現れませんノード
どのノードもその子孫のリーフ ノードまでトラバースし、渡される黒いノードの数は等しくなければなりません
空のノードは黒とみなされます
-
データ構造は次のように表されます:
class Node<T>{ public T value; public Node<T> parent; public boolean isRed; public Node<T> left; public Node<T> right; } RBTree は理論上は依然として Java の赤黒ツリー実装の詳細な分析 (写真) ツリーですが、Java の赤黒ツリー実装の詳細な分析 (写真) 操作の挿入および削除時にツリーのバランスを維持します。つまり、ツリーの高さが [logN, logN+1] であることが保証されます (理論的には、これが発生する可能性があります)極端な場合、RBTree の高さは 2*logN に達しますが、実際にはこれに遭遇するのは困難です)。このように、RBTree の検索時間計算量は常に O(logN) に留まり、理想的な Java の赤黒ツリー実装の詳細な分析 (写真) に近づきます。 RBTree の削除および挿入操作の時間計算量も O(logN) です。 RBTreeの検索動作はJava の赤黒ツリー実装の詳細な分析 (写真)の検索動作となります。
RBTreeの回転操作
回転操作(Rotate)の目的は、ノードの色を定義通りにし、RBTreeの高さをバランス良くすることです。
回転は左回転(左回転)と右回転(右回転)に分かれます。左回転と右回転の見分け方は、回転するノードが左から上に向かって上がることです。親ノードは右回転であり、回転されるノードは右から親ノードに向かって上昇します。親ノードは左巻きです。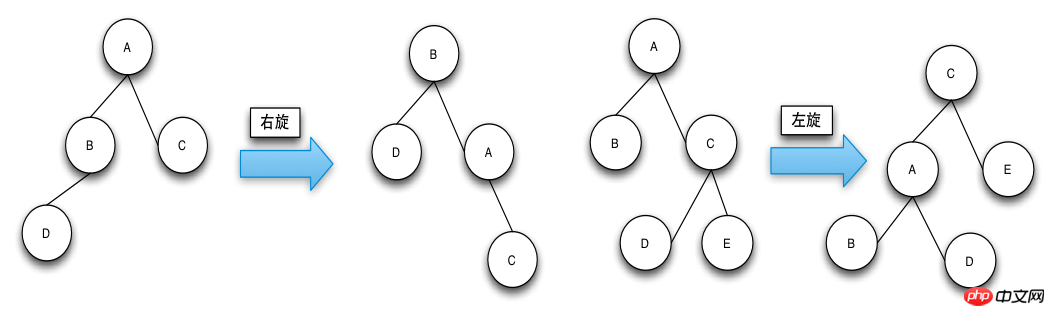
RBTreeの検索操作はJava の赤黒ツリー実装の詳細な分析 (写真)の検索操作と同じです。 Java の赤黒ツリー実装の詳細な分析 (写真)のルックアップオペレーションコードを参照してください。
RBTreeの挿入操作
RBTreeの挿入はJava の赤黒ツリー実装の詳細な分析 (写真)の挿入と同じですが、挿入後にツリーのバランスが崩れる場合がありますので、その際にツリーの回転と色の修復(以下、インサートフィックスと呼びます)が必要になります。 RBTreeの定義に準拠します。
新しく挿入されたノードは赤です。挿入修復操作で黒の親ノードが見つかった場合、修復操作は終了します。換言すれば、修復操作は、親ノードが赤色ノードである場合にのみ挿入する必要がある。
挿入と修復操作は次の 3 つの状況に分けられ、新しく挿入されたノードの親ノードはすべて赤になります:
叔父ノードも赤です。
叔父ノードは空で、祖父母ノード、親ノード、新しいノードが対角線上にあります。
叔父ノードは空であり、祖父母ノード、親ノード、新しいノードはスラッシュ上にありません。
挿入操作-ケース1
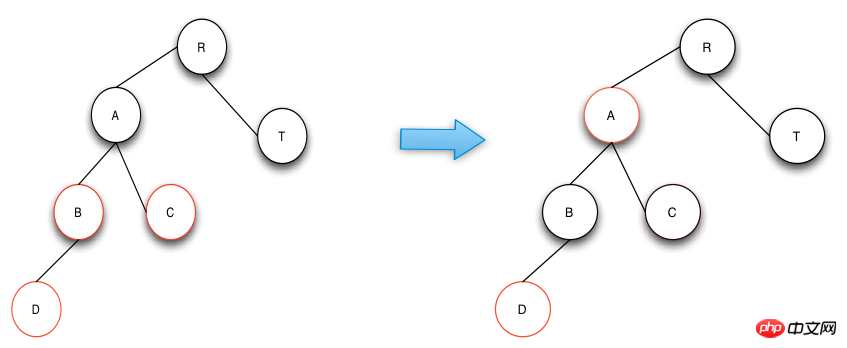
ケース1の操作は、親ノード、叔父ノード、祖父母ノードの色を交換することであり、RBTreeの定義に準拠しています。つまり、高度なバランスが保たれており、修理後の色もRBTreeが定める3番目と4番目の項目を満たしています。次の図では、ノード A は操作が完了すると新しいノードになります。ノード A の親ノードが黒でない場合は、修復操作を続行します。
挿入操作-ケース2
ケース2の操作は、ノードBを右に回転し、親ノードAと色を交換することです。この修復操作により、RBTree の高さと色は赤黒ツリーの定義に準拠します。ノード B と C が両方とも右ノードの場合は、操作を左回転に変更するだけです。
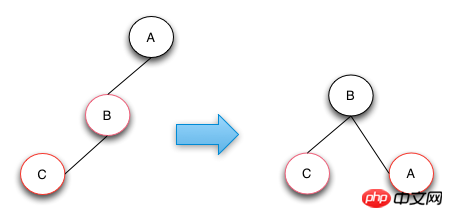
挿入操作-ケース3
ケース3の操作は、Cノードを左回転させてケース3からケース2に変換し、ケース2の演算処理を行うものです。ケース 2 の操作では、右回転操作と色の交換を実行して目的を達成します。ツリーの構造が下図のミラー構造であれば、対応する左回転を右回転に、右回転を左回転に変更するだけです。
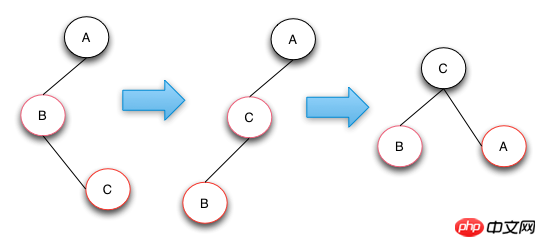
挿入操作の概要
挿入後の修復操作は、関係するノードが赤黒ツリーの定義を満たすと、ルート ノードへのバックトラッキング操作です。上向きにバックトレースする理由は、ケース 1 の操作により親ノード、叔父ノード、祖父ノードの色が変更され、祖父ノードのバランスが崩れる可能性があるためです (赤黒ツリー定義 3)。このとき、祖父ノードを起点として調整（上方向への遡行）する必要があります。
調整後も祖父ノードで祖父の色の問題が発生する場合、定義上、ルート ノードが常に黒になるまで、操作は上向きにトレースされ続けます。上方向のトレース処理では、挿入された 3 つの状況に合わせて調整が行われます。赤黒木の定義が満たされるまで。関係するすべてのノードが赤黒ツリーの定義を満たすまで、修復操作は終了します。
上記の 3 つの状況で対応する操作が右側のサブツリーにある場合は、対応するミラー操作を実行するだけです。
RBTree 削除操作
削除操作は、最初に Java の赤黒ツリー実装の詳細な分析 (写真) 削除操作によって実行する必要があります。削除操作は、リーフ ノードの場合は直接削除されます。ノードの場合、対応する順序トラバーサル サクセサー ノードが削除されるノードの位置を置き換えるのに使用されます。削除後、ツリーを赤黒ツリーの定義に準拠させ、定義を満たす赤黒ツリーの高さのバランスをとるために、削除および修復操作を実行する必要があります。
削除されたノードが赤いノードになるか、ルートノードに到達すると、削除と修復操作は完了します。
削除と修復の操作は黒いノードの削除のみです。黒いノードが削除されると、ツリー全体が RBTree の 4 番目の定義に準拠しなくなります。行う必要があるのは、兄弟ノードから黒ノードを取得することです。兄弟ノードに借用する黒ノードがない場合は、遡って各レベルの黒ノードの数から 1 を引いて全体を作成するだけです。ツリーは赤いノードの定義に準拠します。
削除操作の一般的な考え方は、ツリー内のローカルなバランスを維持するために兄弟ノードから黒いノードを借用することです。ローカルなバランスが達成されているかどうかは、ツリー全体のバランスが取れているかどうかによって決まります。遡及的に上方修正されます。
削除と修復操作は 4 つの状況に分かれています (黒いノードの削除後):
削除されるノードの兄弟ノードは赤いノードです。
削除対象のノードの兄弟ノードは黒色のノードであり、兄弟ノードの子ノードはすべて黒色になります。
調整対象ノードの兄弟ノードは黒ノード、兄弟ノードの左の子ノードは赤、右のノードは黒になります(兄弟ノードの場合は兄弟ノードが右側)。左側にあるのは兄弟ノードです。右側の子ノードは赤で、左側のノードは黒です。
待调整的节点的兄弟节点是黑色的节点，且右子节点是是红色的(兄弟节点在右边)，如果兄弟节点在左边，则就是对应的就是左节点是红色的。
删除操作-case 1
由于兄弟节点是红色节点的时候，无法借调黑节点，所以需要将兄弟节点提升到父节点，由于兄弟节点是红色的，根据RBTree的定义，兄弟节点的子节点是黑色的，就可以从它的子节点借调了。
case 1这样转换之后就会变成后面的case 2，case 3，或者case 4进行处理了。上升操作需要对C做一个左旋操作，如果是镜像结构的树只需要做对应的右旋操作即可。
之所以要做case 1操作是因为兄弟节点是红色的，无法借到一个黑节点来填补删除的黑节点。
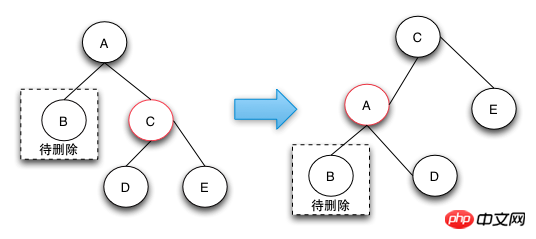
删除操作-case 2
case 2的删除操作是由于兄弟节点可以消除一个黑色节点，因为兄弟节点和兄弟节点的子节点都是黑色的，所以可以将兄弟节点变红，这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点，继续向上调整，直到整颗树的颜色符合RBTree的定义为止。
case 2这种情况下之所以要将兄弟节点变红，是因为如果把兄弟节点借调过来，会导致兄弟的结构不符合RBTree的定义，这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后，达到了局部的平衡了，但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点，接着进行修复操作。
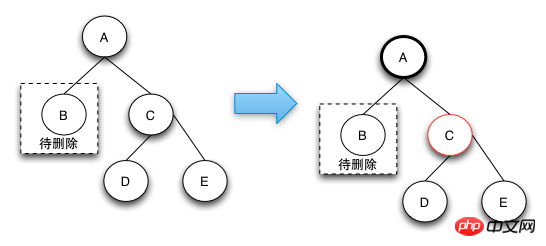
删除操作-case 3
case 3的删除操作是一个中间步骤，它的目的是将左边的红色节点借调过来，这样就可以转换成case 4状态了，在case 4状态下可以将D，E节点都阶段过来，通过将两个节点变成黑色来保证红黑树的整体平衡。
之所以说case-3是一个中间状态，是因为根据红黑树的定义来说，下图并不是平衡的，他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况，是因为可以通过借用侄子节点的红色，变成黑色来符合红黑树定义4.
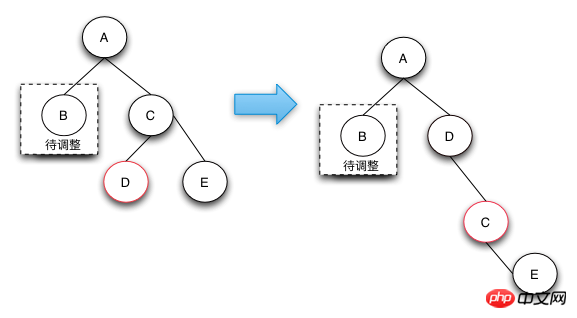
删除操作-case 4
Case 4的操作是真正的节点借调操作，通过将兄弟节点以及兄弟节点的右节点借调过来，并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的，这样的话，整棵树还是符合RBTree的定义的。
Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑，且子节点不全部为黑，才有可能借调到两个节点来做黑节点使用，从而保持整棵树都符合红黑树的定义。
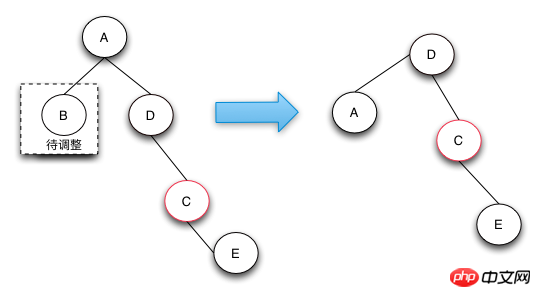
删除操作的总结
红黑树的删除操作是最复杂的操作，复杂的地方就在于当删除了黑色节点的时候，如何从兄弟节点去借调节点，以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的，这样只能通过选择操作让他上升到父节点，而由于它是红节点，所以它的子节点就是黑的，可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理，当所以的兄弟节点的子节点都是黑色节点时，可以直接将兄弟节点变红，这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的，需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红，右红左黑)这两种情况，可以先将前面的情况通过选择转换为后一种情况，在后一种情况下，因为兄弟节点为黑，兄弟节点的右节点为红，可以借调出两个节点出来做黑节点，这样就可以保证删除了黑节点，整棵树还是符合红黑树的定义的，因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色，或者追溯调整到了root节点，这时删除的修复操作完毕。
RBTree的Java实现
public class RBTreeNode<T extends Comparable<T>> {
private T value;//node value
private RBTreeNode<T> left;//left child pointer
private RBTreeNode<T> right;//right child pointer
private RBTreeNode<T> parent;//parent pointer
private boolean red;//color is red or not red
public RBTreeNode(){}
public RBTreeNode(T value){this.value=value;}
public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}
public T getValue() {
return value;
}
void setValue(T value) {
this.value = value;
}
RBTreeNode<T> getLeft() {
return left;
}
void setLeft(RBTreeNode<T> left) {
this.left = left;
}
RBTreeNode<T> getRight() {
return right;
}
void setRight(RBTreeNode<T> right) {
this.right = right;
}
RBTreeNode<T> getParent() {
return parent;
}
void setParent(RBTreeNode<T> parent) {
this.parent = parent;
}
boolean isRed() {
return red;
}
boolean isBlack(){
return !red;
}
/**
* is leaf node
**/
boolean isLeaf(){
return left==null && right==null;
}
void setRed(boolean red) {
this.red = red;
}
void makeRed(){
red=true;
}
void makeBlack(){
red=false;
}
@Override
public String toString(){
return value.toString();
}
}
public class RBTree<T extends Comparable<T>> {
private final RBTreeNode<T> root;
//node number
private java.util.concurrent.atomic.AtomicLong size =
new java.util.concurrent.atomic.AtomicLong(0);
//in overwrite mode,all node's value can not has same value
//in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
private volatile boolean overrideMode=true;
public RBTree(){
this.root = new RBTreeNode<T>();
}
public RBTree(boolean overrideMode){
this();
this.overrideMode=overrideMode;
}
public boolean isOverrideMode() {
return overrideMode;
}
public void setOverrideMode(boolean overrideMode) {
this.overrideMode = overrideMode;
}
/**
* number of tree number
* @return
*/
public long getSize() {
return size.get();
}
/**
* get the root node
* @return
*/
private RBTreeNode<T> getRoot(){
return root.getLeft();
}
/**
* add value to a new node,if this value exist in this tree,
* if value exist,it will return the exist value.otherwise return null
* if override mode is true,if value exist in the tree,
* it will override the old value in the tree
*
* @param value
* @return
*/
public T addNode(T value){
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* find the value by give value(include key,key used for search,
* other field is not used,@see compare method).if this value not exist return null
* @param value
* @return
*/
public T find(T value){
RBTreeNode<T> dataRoot = getRoot();
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
dataRoot = dataRoot.getRight();
}else if(cmp>0){
dataRoot = dataRoot.getLeft();
}else{
return dataRoot.getValue();
}
}
return null;
}
/**
* remove the node by give value,if this value not exists in tree return null
* @param value include search key
* @return the value contain in the removed node
*/
public T remove(T value){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
parent = dataRoot;
dataRoot = dataRoot.getRight();
}else if(cmp>0){
parent = dataRoot;
dataRoot = dataRoot.getLeft();
}else{
if(dataRoot.getRight()!=null){
RBTreeNode<T> min = removeMin(dataRoot.getRight());
//x used for fix color balance
RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
boolean isParent = min.getRight()==null;
min.setLeft(dataRoot.getLeft());
setParent(dataRoot.getLeft(),min);
if(parent.getLeft()==dataRoot){
parent.setLeft(min);
}else{
parent.setRight(min);
}
setParent(min,parent);
boolean curMinIsBlack = min.isBlack();
//inherit dataRoot's color
min.setRed(dataRoot.isRed());
if(min!=dataRoot.getRight()){
min.setRight(dataRoot.getRight());
setParent(dataRoot.getRight(),min);
}
//remove a black node,need fix color
if(curMinIsBlack){
if(min!=dataRoot.getRight()){
fixRemove(x,isParent);
}else if(min.getRight()!=null){
fixRemove(min.getRight(),false);
}else{
fixRemove(min,true);
}
}
}else{
setParent(dataRoot.getLeft(),parent);
if(parent.getLeft()==dataRoot){
parent.setLeft(dataRoot.getLeft());
}else{
parent.setRight(dataRoot.getLeft());
}
//current node is black and tree is not empty
if(dataRoot.isBlack() && !(root.getLeft()==null)){
RBTreeNode<T> x = dataRoot.getLeft()==null
? parent :dataRoot.getLeft();
boolean isParent = dataRoot.getLeft()==null;
fixRemove(x,isParent);
}
}
setParent(dataRoot,null);
dataRoot.setLeft(null);
dataRoot.setRight(null);
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
size.decrementAndGet();
return dataRoot.getValue();
}
}
return null;
}
/**
* fix remove action
* @param node
* @param isParent
*/
private void fixRemove(RBTreeNode<T> node,boolean isParent){
RBTreeNode<T> cur = isParent ? null : node;
boolean isRed = isParent ? false : node.isRed();
RBTreeNode<T> parent = isParent ? node : node.getParent();
while(!isRed && !isRoot(cur)){
RBTreeNode<T> sibling = getSibling(cur,parent);
//sibling is not null,due to before remove tree color is balance
//if cur is a left node
boolean isLeft = parent.getRight()==sibling;
if(sibling.isRed() && !isLeft){//case 1
//cur in right
parent.makeRed();
sibling.makeBlack();
rotateRight(parent);
}else if(sibling.isRed() && isLeft){
//cur in left
parent.makeRed();
sibling.makeBlack();
rotateLeft(parent);
}else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
sibling.makeRed();
cur = parent;
isRed = cur.isRed();
parent=parent.getParent();
}else if(isLeft && !isBlack(sibling.getLeft())
&& isBlack(sibling.getRight())){//case 3
sibling.makeRed();
sibling.getLeft().makeBlack();
rotateRight(sibling);
}else if(!isLeft && !isBlack(sibling.getRight())
&& isBlack(sibling.getLeft()) ){
sibling.makeRed();
sibling.getRight().makeBlack();
rotateLeft(sibling);
}else if(isLeft && !isBlack(sibling.getRight())){//case 4
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getRight().makeBlack();
rotateLeft(parent);
cur=getRoot();
}else if(!isLeft && !isBlack(sibling.getLeft())){
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getLeft().makeBlack();
rotateRight(parent);
cur=getRoot();
}
}
if(isRed){
cur.makeBlack();
}
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
}
//get sibling node
private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
parent = node==null ? parent : node.getParent();
if(node==null){
return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
}
if(node==parent.getLeft()){
return parent.getRight();
}else{
return parent.getLeft();
}
}
private boolean isBlack(RBTreeNode<T> node){
return node==null || node.isBlack();
}
private boolean isRoot(RBTreeNode<T> node){
return root.getLeft() == node && node.getParent()==null;
}
/**
* find the successor node
* @param node current node's right node
* @return
*/
private RBTreeNode<T> removeMin(RBTreeNode<T> node){
//find the min node
RBTreeNode<T> parent = node;
while(node!=null && node.getLeft()!=null){
parent = node;
node = node.getLeft();
}
//remove min node
if(parent==node){
return node;
}
parent.setLeft(node.getRight());
setParent(node.getRight(),parent);
//don't remove right pointer,it is used for fixed color balance
//node.setRight(null);
return node;
}
private T addNode(RBTreeNode<T> node){
node.setLeft(null);
node.setRight(null);
node.setRed(true);
setParent(node,null);
if(root.getLeft()==null){
root.setLeft(node);
//root node is black
node.setRed(false);
size.incrementAndGet();
}else{
RBTreeNode<T> x = findParentNode(node);
int cmp = x.getValue().compareTo(node.getValue());
if(this.overrideMode && cmp==0){
T v = x.getValue();
x.setValue(node.getValue());
return v;
}else if(cmp==0){
//value exists,ignore this node
return x.getValue();
}
setParent(node,x);
if(cmp>0){
x.setLeft(node);
}else{
x.setRight(node);
}
fixInsert(node);
size.incrementAndGet();
}
return null;
}
/**
* find the parent node to hold node x,if parent value equals x.value return parent.
* @param x
* @return
*/
private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> child = dataRoot;
while(child!=null){
int cmp = child.getValue().compareTo(x.getValue());
if(cmp==0){
return child;
}
if(cmp>0){
dataRoot = child;
child = child.getLeft();
}else if(cmp<0){
dataRoot = child;
child = child.getRight();
}
}
return dataRoot;
}
/**
* red black tree insert fix.
* @param x
*/
private void fixInsert(RBTreeNode<T> x){
RBTreeNode<T> parent = x.getParent();
while(parent!=null && parent.isRed()){
RBTreeNode<T> uncle = getUncle(x);
if(uncle==null){//need to rotate
RBTreeNode<T> ancestor = parent.getParent();
//ancestor is not null due to before before add,tree color is balance
if(parent == ancestor.getLeft()){
boolean isRight = x == parent.getRight();
if(isRight){
rotateLeft(parent);
}
rotateRight(ancestor);
if(isRight){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}else{
boolean isLeft = x == parent.getLeft();
if(isLeft){
rotateRight(parent);
}
rotateLeft(ancestor);
if(isLeft){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}
}else{//uncle is red
parent.setRed(false);
uncle.setRed(false);
parent.getParent().setRed(true);
x=parent.getParent();
parent = x.getParent();
}
}
getRoot().makeBlack();
getRoot().setParent(null);
}
/**
* get uncle node
* @param node
* @return
*/
private RBTreeNode<T> getUncle(RBTreeNode<T> node){
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> ancestor = parent.getParent();
if(ancestor==null){
return null;
}
if(parent == ancestor.getLeft()){
return ancestor.getRight();
}else{
return ancestor.getLeft();
}
}
private void rotateLeft(RBTreeNode<T> node){
RBTreeNode<T> right = node.getRight();
if(right==null){
throw new java.lang.IllegalStateException("right node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setRight(right.getLeft());
setParent(right.getLeft(),node);
right.setLeft(node);
setParent(node,right);
if(parent==null){//node pointer to root
//right raise to root node
root.setLeft(right);
setParent(right,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(right);
}else{
parent.setRight(right);
}
//right.setParent(parent);
setParent(right,parent);
}
}
private void rotateRight(RBTreeNode<T> node){
RBTreeNode<T> left = node.getLeft();
if(left==null){
throw new java.lang.IllegalStateException("left node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setLeft(left.getRight());
setParent(left.getRight(),node);
left.setRight(node);
setParent(node,left);
if(parent==null){
root.setLeft(left);
setParent(left,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(left);
}else{
parent.setRight(left);
}
setParent(left,parent);
}
}
private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
if(node!=null){
node.setParent(parent);
if(parent==root){
node.setParent(null);
}
}
}
/**
* debug method,it used print the given node and its children nodes,
* every layer output in one line
* @param root
*/
public void printTree(RBTreeNode<T> root){
java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
if(root==null){
return ;
}
queue.add(root);
boolean firstQueue = true;
while(!queue.isEmpty() || !queue2.isEmpty()){
java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
RBTreeNode<T> n = q.poll();
if(n!=null){
String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft()
? " LE" : " RI");
String pstr = n.getParent()==null ? "" : n.getParent().toString();
String cstr = n.isRed()?"R":"B";
cstr = n.getParent()==null ? cstr : cstr+" ";
System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
if(n.getLeft()!=null){
(firstQueue ? queue2 : queue).add(n.getLeft());
}
if(n.getRight()!=null){
(firstQueue ? queue2 : queue).add(n.getRight());
}
}else{
System.out.println();
firstQueue = !firstQueue;
}
}
}
public static void main(String[] args) {
RBTree<String> bst = new RBTree<String>();
bst.addNode("d");
bst.addNode("d");
bst.addNode("c");
bst.addNode("c");
bst.addNode("b");
bst.addNode("f");
bst.addNode("a");
bst.addNode("e");
bst.addNode("g");
bst.addNode("h");
bst.remove("c");
bst.printTree(bst.getRoot());
}
}代码调试的时候，printTree输出格式如下:
d(B) b(B d LE) g(R d RI) a(R b LE) e(B g LE) h(B g RI) f(R e RI)
括号左边表示元素的内容。括号内的第一个元素表示颜色，B表示black，R表示red；第二个元素表示父元素的值；第三个元素表示左右，LE表示在父元素的左边。RI表示在父元素的右边。
第一个元素d是root节点，由于它没有父节点，所以括号内只有一个元素。
总结
作为平衡二叉查找树里面众多的实现之一，红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念，通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树，旋转是一个必不可少的操作。通过旋转可以降低树的高度，在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解，这时要注意记住一点：操作之前红黑树是平衡的，颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色，要达到这个目的，就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转，一旦借调了别的节点，删除和插入的节点就会达到局部的平衡（局部符合红黑树的定义），但是被借调的节点就不会平衡了，这时就需要以被借调的节点为起点继续进行调整，直到整棵树都是平衡的。在整个修复的过程中，插入具体的分为3种情况，删除分为4种情况。
整个红黑树的查找，插入和删除都是O(logN)的，原因就是整个红黑树的高度是logN，查找从根到叶，走过的路径是树的高度，删除和插入操作是从叶到根的，所以经过的路径都是logN。
以上がJava の赤黒ツリー実装の詳細な分析 (写真)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。