ホームページ >バックエンド開発 >Python チュートリアル >Python 機械学習デシジョン ツリーの詳細な紹介
Python 機械学習デシジョン ツリーの詳細な紹介
- 高洛峰オリジナル
- 2017-03-19 14:20:142122ブラウズ
デシジョン ツリー (DT) は、分類と回帰に使用される教師なし学習方法です。
利点: 計算の複雑さは高くなく、出力結果は理解しやすく、中間値の欠落の影響を受けず、無関係な特徴データを処理できます
欠点: 過剰一致の問題が発生する可能性があります
適用可能なデータ型: 数値および標準ソースコードのダウンロードを入力 https://www.manning.com/books/machine-learning-in-action
デモを実行する
キーアルゴリズム
関数createBranchを分割する最適な特徴を見つけて、戻り結果をブランチノードに追加します
returnブランチノード
対応するコード def createTree(dataSet,labels):
class
List
if classList.
count(classList[0 ]) == len(classList): 返された分類リストのカウント型が同じ場合は、この型を返します。子ノードが分類できるかどうか、分類できる場合は 1 つのタイプを返します。そうでない場合は、
再帰下方分類 dataSet にそれ以上の特徴がありません。要素が 1 つしかない場合は、 return MajorCnt(classList) bestFeat = BESTFEATURETOSPLIT(DATASET)最適な機能インデックスBestFeatLabel = labels [bestfeat]を選択し、このラベルフリッパーまたはサーフェスを取得しますmytree = {bestfeatlabel:{}}たとえば、datasetにある
uniquevals = set set (featValues) set uniqueVALS の for 値の種類に応じて分類されます: Sublabels = label [:] #copy all oflabels, so time do台無しに既存のラベル mytree [Value] [Value] = CreateTree ( splitdataset (dataset , bestFeat, value),subLabels) return myTree
データセットを分割する前後の情報の変化を情報ゲインと呼びます。データセットを分割する最大の原理は、順序付けされていないデータをより順序付けすることです。 これは、パイカットの原則として理解されます:
単位エントロピーを使用して、情報の複雑さと量を説明します。 ケーキの密度に対応して、同じ密度の垂直にカットされたケーキであれば、
各部分の重量 g = 合計 G * 大圏におけるその割合! 同様に、除算後の情報エントロピーが同じである場合、データの各小さな部分の小さい h = pro * 合計 H、および合計 h[i] = H となります。
ただし、必要なのはその逆です。必要なのは、同じ情報エントロピーではなく、不均一な情報です。たとえば、上の緑のものは草の餡、黄色のものはリンゴの餡、青のものは紫色のサツマイモの餡である可能性があり、それぞれ密度が異なります。 !
正しく分割する必要があります!それを整理して、さまざまな詰め物を近似する線を見つけます。 ここでの小さな h は最小化され、最終的には面積が変化しない状態で合計 H が最小値に近づきます。これが最適化問題の解を求めます。
デバッグプロセス
calcShannonEnt
log(prob,2) log(1,2) = 0;2^0=1 でなければならないため、prob
dataSet の featVec の 25 行: 頻度のカウントfor prop
chooseBestFeatureToSplit()
0.9709505944546686 = calcShannonEnt(dataSet)
#データセットの各サブ項目が同じカテゴリに属しているかどうかを検出します: 値がすべて a である場合、結果はすべて y または n になります。したがって、パラメーターは 2 つだけ入力されます
0.5509775004326937 = += prob * calcShannonEnt(subDataSet) サブセットを分離した後、確率 * シャノン ドロップ、取得された合計、元の全体的なシャノンのドロップ率
# 数据越接近,香浓熵值越少,越接近0 ,越不同,越多分逻辑,香浓熵就越大 # 只计算 其dataSet的featVec[-1] 结果标签 def calcShannonEnt(dataSet):
0.4199730940219749 infoGain = BaseEntropy - newEntropy
概要:
最初はコードが理解できず、何をするのか理解できませんでした。分類、私たちの目標は、大量のデータを分類し、ラベルでラベルを付けることです。
k-nearby assign([0, 0], group,labels, 3) と同様に、新しいデータ [0,0] がグループに分類され、k=3 近傍アルゴリズムに従ってデータにラベルが付けられることを意味します。 グループがラベルに対応!
後で見ました
そして、データdataSetがディメンションの値を意味し、最後のものが魚であるかどうか、結果ラベルであることを理解しました
それで、私たちは次のようにする必要があります各次元を切り出します + 結果のラベルは比較と分類のために 2 次元配列に変換されます。テストでは、最初の n 次元の値をベクトルに入力し、出力は「はい」か「いいえ」になります。一見するとめまいがするように見えますが、コードを見るだけで簡単に理解できるので、考えを整理する必要があります。
ターゲットと初期データを理解すると、classList が結果ラベルであることがわかります。 、分類対象のデータセットに対応する対応する結果ラベルです
、ラベルは開始データセットの次元に対応する特徴名です。特徴の名前です。strname
bestFeatLabel は、最適な分類特徴の次元名です。 N
featValues は最初の次元または 2 番目の次元であり、bestFeatLabel の次元の下にある値の配列です。新しい分類比較を行うために使用されるのは、このディメンションの下のグループです。
uniqueVals は set を使用して同じカテゴリに属するかどうかを判断します。
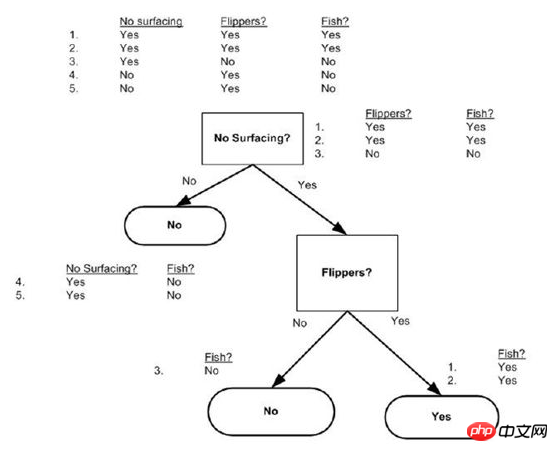
例: dataSet = [[1, 1, 'yes'],[0, 1, 'yes'],[1, 0, 'no'] ,[1, 0 , 'no'],[0, 0, 'no']]
Labels = ['no surfaceing','flippers',]
createTree like this:{'flippers': {0: 'no ', 1: 'yes'}} は、表面化しない次元を直接省略します
以上がPython 機械学習デシジョン ツリーの詳細な紹介の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

