Python でバイナリ ヒープを実装する方法

バイナリ ヒープは特別な種類のヒープです。バイナリ ヒープは、完全なバイナリ ツリー (バイナリ ツリー)、またはほぼ完全なバイナリ ツリー (バイナリ ツリー) です。バイナリ ヒープには、max-heap と min-heap の 2 種類があります。最大ヒープ: 親ノードのキー値は常に​​子ノードのキー値以上です。最小ヒープ: 親ノードのキー値は常に​​子ノードのキー値以下です。

優先キューのバイナリヒープ実装

前の章では、「先入れ先出し」 (FIFO) のデータ構造を学習しました。 >)。 「Priority Queue」(Priority Queue) と呼ばれるキューのバリエーションがあります。優先キューのデキュー (Dequeue) 操作はキューと同じで、キューの先頭からデキューされます。ただし、優先キュー内では、要素の順序は「優先度」によって決定されます: 高-優先度の高い要素はキューの先頭に並べ替えられ、優先度の低い要素は最後に並べ替えられます。このように、優先度キューのエンキュー (Enqueue) 操作はより複雑になり、要素は優先度に従って可能な限りキューに入れられる必要があります。次のセクションでは、優先キューがグラフ アルゴリズムにとって有用なデータ構造であることがわかります。 FIFO）的数据结构：队列（Queue）。队列有一种变体叫做“优先队列”（Priority Queue）。优先队列的出队（Dequeue）操作和队列一样，都是从队首出队。但在优先队列的内部，元素的次序却是由“优先级”来决定：高优先级的元素排在队首，而低优先级的元素则排在后面。这样，优先队列的入队（Enqueue）操作就比较复杂，需要将元素根据优先级尽量排到队列前面。我们将会发现，对于下一节要学的图算法中的优先队列是很有用的数据结构。

我们很自然地会想到用排序算法和队列的方法来实现优先队列。但是，在列表里插入一个元素的时间复杂度是O(n)，对列表进行排序的时间复杂度是O(nlogn)。我们可以用别的方法来降低时间复杂度。一个实现优先队列的经典方法便是采用二叉堆（Binary Heap）。二叉堆能将优先队列的入队和出队复杂度都保持在O(logn)。

二叉堆的有趣之处在于，其逻辑结构上像二叉树，却是用非嵌套的列表来实现。二叉堆有两种：键值总是最小的排在队首称为“最小堆（min heap）”，反之，键值总是最大的排在队首称为“最大堆（max heap）”。在这一节里我们使用最小堆。

二叉堆的操作

二叉堆的基本操作定义如下：

1. BinaryHeap()：创建一个空的二叉堆对象

2. insert(k)：将新元素加入到堆中

3. findMin()：返回堆中的最小项，最小项仍保留在堆中

4. delMin()：返回堆中的最小项，同时从堆中删除

5. isEmpty()：返回堆是否为空

6. size()：返回堆中节点的个数

7. buildHeap(list)：从一个包含节点的列表里创建新堆

下面所示代码是二叉堆的示例。可以看到无论我们以哪种顺序把元素添加到堆里，每次都是移除最小的元素。我们接下来要来实现这个过程。

from pythonds.trees.binheap import BinHeap

bh = BinHeap()
bh.insert(5)
bh.insert(7)
bh.insert(3)
bh.insert(11)

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

为了更好地实现堆，我们采用二叉树。我们必须始终保持二叉树的“平衡”，就要使操作始终保持在对数数量级上。平衡的二叉树根节点的左右子树的子节点个数相同。在堆的实现中，我们采用“完全二叉树”的结构来近似地实现“平衡”。完全二叉树，指每个内部节点树均达到最大值，除了最后一层可以只缺少右边的若干节点。图 1 所示是一个完全二叉树。

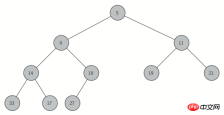
图 1：完全二叉树

有意思的是我们用单个列表就能实现完全树。我们不需要使用节点，引用或嵌套列表。因为对于完全二叉树，如果节点在列表中的下标为 p，那么其左子节点下标为 2p，右节点为 2p+1。当我们要找任何节点的父节点时，可以直接使用 python 的整除。如果节点在列表中下标为n，那么父节点下标为n//2

優先キューを実装するには、ソートアルゴリズムとキューを使用することを当然考えます。ただし、リストへの要素の挿入の時間計算量は O(n) であり、リストの並べ替えの時間計算量は O(nlogn) です。他の方法を使用して、時間の複雑さを軽減できます。優先キューを実装する古典的な方法は、バイナリ ヒープ (Binary Heap) を使用することです。バイナリ ヒープは、優先キューのエンキューとデキューの両方の複雑さを O(logn) に保つことができます。

バイナリ ヒープの興味深い点は、その論理構造はバイナリ ツリーに似ていますが、ネストされていないリストで実装されていることです。バイナリ ヒープには 2 つのタイプがあります。最小のキー値が常にキューの先頭にあるものは「最小ヒープ (min heap)」と呼ばれ、逆に、最大のキー値が常にキューの先頭にあります。キューの先頭の値は「最小ヒープ (max heap)」と呼ばれます。このセクションでは、min-heap を使用します。

バイナリヒープの操作

バイナリヒープの基本的な操作定義は次のとおりです:

1. BinaryHeap(): Create空のバイナリ ヒープ オブジェクト

2. insert(k): ヒープに新しい要素を追加します

3. findMin(): ヒープ内の最小の項目を返し、その最小の項目はヒープに残ります
4. 🎜delMin(): ヒープ内の最小の項目を返し、ヒープから削除しますheap 🎜
5. 🎜isEmpty(): ヒープが空かどうかを返します🎜
6. 🎜size(): サイズを返しますヒープ内のノードの番号🎜
7. 🎜buildHeap(list): ノードを含むリストから新しいヒープを作成します🎜

🎜示されているコード以下はバイナリのヒープの例です。どの順序で要素をヒープに追加しても、毎回最小の要素が削除されることがわかります。次にこの処理を実装していきます。 🎜

🎜

class BinHeap:
  def init(self):
    self.heapList = [0]
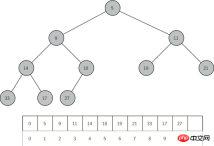
    self.currentSize = 0

🎜 ヒープをより適切に実装するために、バイナリ ツリーを使用します。二分木の「バランス」を常に維持し、常に対数スケールでの操作を維持する必要があります。バランスの取れたバイナリ ツリーには、ルート ノードの左右のサブツリーに同じ数の子ノードがあります。ヒープの実装では、「完全なバイナリ ツリー」の構造を使用して、ほぼ「バランス」を実現します。完全なバイナリ ツリーとは、各内部ノード ツリーがその最大値に達することを意味します。ただし、最後のレベルには右側のいくつかのノードしか欠けることはありません。図 1 は、完全なバイナリ ツリーを示しています。 🎜🎜🎜🎜図 1: 完全なバイナリ ツリー🎜🎜興味深いことに、単一のリストで完全なツリーを実装できます。ノード、参照、またはネストされたリストを使用する必要はありません。完全な二分木の場合、リスト内のノードの添え字が p の場合、その左側の子ノードの添え字は 2p で、右側のノードの添え字は 2p+1 となるためです。任意のノードの親ノードを見つけたい場合は、Python の整数除算を直接使用できます。リスト内でノードのインデックスが n である場合、親ノードのインデックスは n//2 になります。図 2 は、完全なバイナリ ツリーとツリーのリスト表現を示しています。親ノードと子ノード間の 2p および 2p+1 関係に注目してください。完全なツリーのリスト表現は完全なバイナリ ツリーのプロパティを組み合わせているため、単純な数学的手法を使用して完全なツリーを効率的に走査することができます。これにより、バイナリ ヒープを効率的に実装することもできます。 🎜🎜🎜ヒープ順序のプロパティ🎜🎜🎜 ヒープに要素を格納する方法は、ヒープの順序によって異なります。いわゆるヒープ順序は、ヒープ内の任意のノード x について、その親ノード p のキー値が x のキー値以下であることを意味します。図 2 は、ヒープ順序付けされたプロパティを持つ完全なバイナリ ツリーを示しています。 🎜🎜🎜🎜🎜図 2: 完全なツリーとそのリスト表現🎜🎜🎜バイナリ ヒープ操作の実装🎜🎜

接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据，构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1 所示的是构造二叉堆的 python 代码。注意到二叉堆的heaplist并没有用到，但为了后面代码可以方便地使用整除，我们仍然保留它。

Listing 1

class BinHeap:
  def init(self):
    self.heapList = [0]
    self.currentSize = 0

我们接下来要实现的是insert方法。首先，为了满足“完全二叉树”的性质，新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾，显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小，可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

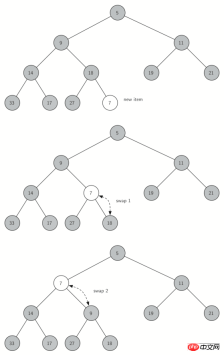
图 3：新节点“上浮”到其正确位置

当我们让一个元素“上浮”时，我们要保证新节点与父节点以及其他兄弟节点之间的堆次序。当然，如果新节点非常小，我们仍然需要将它交换到其他层。事实上，我们需要不断交换，直到到达树的顶端。Listing 2 所示的是“上浮”方法，它把一个新节点“上浮”到其正确位置来满足堆次序。这里很好地体现了我们之前在headlist中没有用到的元素 0 的重要性。这样只需要做简单的整除，将当前节点的下标除以 2，我们就能计算出任何节点的父节点。

在Listing 3 中，我们已经可以写出insert方法的代码。insert里面很大一部分工作是由percUp函数完成的。当树添加新节点时，调用percUp就可以将新节点放到正确的位置上。

Listing 2

def percUp(self,i):
  while i // 2 > 0:
   if self.heapList[i] < self.heapList[i // 2]:
     tmp = self.heapList[i // 2]
     self.heapList[i // 2] = self.heapList[i]
     self.heapList[i] = tmp
   i = i // 2

Listing 3

def insert(self,k):
  self.heapList.append(k)
  self.currentSize = self.currentSize + 1
  self.percUp(self.currentSize)

我们已经写好了insert方法，那再来看看delMin方法。堆次序要求根节点是树中最小的元素，因此很容易找到最小项。比较困难的是移走根节点的元素后如何保持堆结构和堆次序，我们可以分两步走。首先，用最后一个节点来代替根节点。移走最后一个节点保持了堆结构的性质。这么简单的替换，还是会破坏堆次序。那么第二步，将新节点“下沉”来恢复堆次序。图 4 所示的是一系列交换操作来使新节点“下沉”到正确的位置。

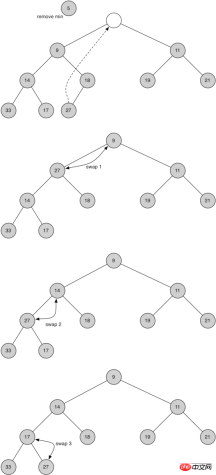
图 4：替换后的根节点下沉

为了保持堆次序，我们需将新的根节点沿着一条路径“下沉”，直到比两个子节点都小。在选择下沉路径时，如果新根节点比子节点大，那么选择较小的子节点与之交换。Listing 4 所示的是新节点下沉所需的percDown和minChild方法的代码。

Listing 4

def percDown(self,i):
  while (i * 2) <= self.currentSize:
    mc = self.minChild(i)
    if self.heapList[i] > self.heapList[mc]:
      tmp = self.heapList[i]
      self.heapList[i] = self.heapList[mc]
      self.heapList[mc] = tmp
    i = mc

def minChild(self,i):
  if i * 2 + 1 > self.currentSize:
    return i * 2
  else:
    if self.heapList[i*2] < self.heapList[i*2+1]:
      return i * 2
    else:
      return i * 2 + 1

Listing 5 所示的是delMin操作的代码。可以看到比较麻烦的地方由一个辅助函数来处理，即percDown。

Listing 5

def delMin(self):
  retval = self.heapList[1]
  self.heapList[1] = self.heapList[self.currentSize]
  self.currentSize = self.currentSize - 1
  self.heapList.pop()
  self.percDown(1)
  return retval

关于二叉堆的最后一部分便是找到从无序列表生成一个“堆”的方法。我们首先想到的是，将无序列表中的每个元素依次插入到堆中。对于一个排好序的列表，我们可以用二分搜索找到合适的位置，然后在下一个位置插入这个键值到堆中，时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动，为新节点腾出位置，时间复杂度为O(n)。因此用insert方法的总开销是O(nlogn)。其实我们能直接将整个列表生成堆，将总开销控制在O(n)。Listing 6 所示的是生成堆的操作。

Listing 6

def buildHeap(self,alist):
  i = len(alist) // 2
  self.currentSize = len(alist)
  self.heapList = [0] + alist[:]
  while (i > 0):
    self.percDown(i)
    i = i - 1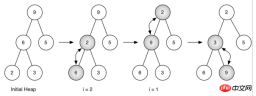

图 5：将列表[ 9, 6, 5, 2, 3]生成一个二叉堆

图 5 所示的是利用buildHeap方法将最开始的树[ 9, 6, 5, 2, 3]中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始，然后回溯到根节点，但percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树，任何在中间的节点都是叶节点，因此没有子节点。注意，当i=1时，我们从根节点开始下沉，这就需要进行大量的交换操作。可以看到，图 5 最右边的两颗树，首先 9 从根节点的位置移走，移到下一层级之后，percDown进一步检查它此时的子节点，保证它下降到不能再下降为止，即下降到正确的位置。然后进行第二次交换，9 和 3 的交换。由于 9 已经移到了树最底层的层级，便无法进一步交换了。比较一下列表表示法和图 5 所示的树表示法进行的一系列交换还是很有帮助的。

i = 2 [0, 9, 5, 6, 2, 3]
i = 1 [0, 9, 2, 6, 5, 3]
i = 0 [0, 2, 3, 6, 5, 9]

下列所示的代码是完全二叉堆的实现。

def insert(self,k):
   self.heapList.append(k)
   self.currentSize = self.currentSize + 1
   self.percUp(self.currentSize)

  def percDown(self,i):
   while (i * 2) <= self.currentSize:
     mc = self.minChild(i)
     if self.heapList[i] > self.heapList[mc]:
       tmp = self.heapList[i]
       self.heapList[i] = self.heapList[mc]
       self.heapList[mc] = tmp
     i = mc

  def minChild(self,i):
   if i * 2 + 1 > self.currentSize:
     return i * 2
   else:
     if self.heapList[i*2] < self.heapList[i*2+1]:
       return i * 2
     else:
       return i * 2 + 1

  def delMin(self):
   retval = self.heapList[1]
   self.heapList[1] = self.heapList[self.currentSize]
   self.currentSize = self.currentSize - 1

能在O(n)的开销下能生成二叉堆看起来有点不可思议，其证明超出了本书的范围。但是，要理解用O(n)的开销能生成堆的关键是因为logn因子基于树的高度。而对于buildHeap里的许多操作，树的高度比logn要小。

以上がPython でバイナリ ヒープを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。