Python はハノイ塔の再帰アルゴリズムを実装します

再帰を学んでいたとき、ハノイの塔という演習があり、ハノイの塔はコンピュータの再帰アルゴリズムを学ぶための古典的な入門例になるはずだったので、自分の意見を表現するためにブログを書くことができると思いました。このマークダウンエディタの使い方がまだわかりません。少し書き方が悪いかもしれませんが、ご容赦ください

ハノイの塔は、を使用しています。塔の最後の部分を分割するための真ん中の柱。左側の柱の円盤は大きいものから小さいものへと積み重ねられています。はっきり言って、c は元の a と同じであるはずです

ナンセンスな話はやめてください。 , まずはコードを示してみましょう

def move(n, a, buffer, c):
  if(n == 1):
    print(a,"->",c)
    return
  move(n-1, a, c, buffer)
  move(1, a, buffer, c)
  move(n-1, buffer, a, c)
move(3, "a", "b", "c")

一つ目は定義です 移動関数、4つのパラメータはそれぞれa列のプレートの数を表し、バッファは列bです わかりやすいようにbufferと名付けました。名前が示すように、これは a を c に移動するバッファです。そして c がターゲット列です
次に関数コードを読んでみましょう
再帰の一般的な書き方は、再帰ループを終了する条件が必要であるということです。列 a のプレートの数が 1 であると判断された場合、再帰は終了し、列 a にプレートが 1 つしかない場合は、a が c に移動されている必要があります。再帰は実際には非常に抽象的なアルゴリズムです。ハノイの塔について考えるには、上のプレートを 2 つと考えます

。

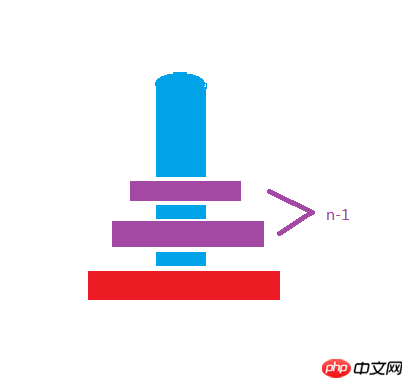
プレートの数は気にしません。毎回の操作は、一番下のプレートを列 b のバッファーを介して列 c に移動することです。
子供たちの靴は、なぜジャン ジー を動かす必要があるのか​​を考えているはずです。実際、これはハノイの塔ゲームをプレイすると、上記のすべてを常に動かすというルールがわかります。あらゆる方法で物を b に移動し、次に a にある最後の最大のものを c に移動し、次に b にある物を c に移動するのに知恵を絞ってください。この時点で、次のことがわかります。 b 上の現在の n-1 を最初に格納し、次に b の最大のものと最後のものを c に移動する必要があります。移動メソッドもここで抽象化できます。これに基づいてプログラムのアルゴリズムを設計できます

以下でこれを実行してみましょう

move(n-1, a, c,buffer)

このコードの意味は、今の抽象的な考え方を使用してください。 n-1 を先ほど述べた a 柱の上に移動するには、Larger ルールに従って c を介して最初にバッファに移動します。この関数は再帰に入ります。

move(1, a,buffer, c)

上記のステートメントの実行が完了したとき、つまり、n-1 個のプレートの再帰的移動が完了した後、このステートメントを実行すると、上のプレートが移動します。いわゆるボトムプレートである c への列です

move(n-1,buffer,a,c)

最後のステップは、a 上のすべての n-1 項目をバッファーに移動することです。それを渡さなければなりません aがcに移動された場合にのみ、ハノイの塔全体の移動が完了することができます。したがって、最後のステップは、今n-1個のアイテムをバッファゾーンとしてaを介して列cに移動することです
書き留めておきます。列 a に基づいた移動プロセス全体。 例は 3 つあります

/**
我把3个盘子的汉诺塔全部通过代码演示，按缩进原则，每一个缩进即进一个递归函数，每打印一次即中止当前递归,也就是每个print
说明:
  1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果，这里就不写判断了，相信童鞋们也能看懂，也就是n不等与1时就减1进入递归
  2.请注意a,b,c柱每次进入函数的顺序，不要被形参带错路了，看准每次函数参数的实参 
**/
move(3, "a", "b", "c")
n=3:
  //开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
  move(2, "a","c","b")
  n=2:
  //开始进行n=2的一个递归，把当前a('a')柱上的n-1个盘子通过c('b'）移动到b('c')
    move(1, "a", "b", "c")
    n=1:
    //n=2的第一个递归完成,打印结果，执行当前子函数剩余代码
      print("a", "->", "c") 
    move(1, "a", "c", "b")
    n=1:
      print("a", "->", "b")
    move(1, "c", "a", "b")
    n=1:
      print("c", "->", "b")
  　  //到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
  print("a", "->", "c")
  //到这里完成移动a柱上的最后一个盘子到c柱上 
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
  move(1, "b", "c", "a")
  n=1:
  //n=2 的第二个递归完成，打印结果并执行当前子函数的剩余代码
    print("b", "->", "a")
  move(1, "b", "a", "c")
  n=1:
    print("b", "->", "c")
  move(1, "a", "b", "c")
  n=1:
    print("a", "->", "c")
    //到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成

最終的な印刷結果は次のとおりです:

子供たちがハノイ塔の再帰アルゴリズムの原理を理解した後、次のことができます。プログラムを書いて試してみましょう。これは Python の再帰が他の言語で実装できる理由です。ハノイの塔は、プログラミングにおける再帰の重要性を理解するのに役立ちます。自明のことです！

ハノイ塔の再帰アルゴリズムの Python 実装に関連するその他の記事については、PHP 中国語 Web サイトに注目してください。