ホームページ >Java >&#&チュートリアル >Java 改良章 (27)-----ツリーマップ
Java 改良章 (27)-----ツリーマップ
- 黄舟オリジナル
- 2017-02-11 09:59:571380ブラウズ
----------------------------------------------------- -------------------------------------------------- -------------------------------------------------- --------------------------------
TreeMapの実装は赤黒の実装です実際、このブログ投稿の名前は「赤黒ツリー アルゴリズムに基づいた TreeMap の実装の分析」です。 Java 改善シリーズのブログ投稿と一貫性を持たせるため、TreeMap と呼ぶことをお勧めします。このブログ投稿を通じて、次の知識ポイントを得ることができます:
1. 赤黒木の基本概念。
2. 赤黒ツリーのノードの追加とノードの削除の実装プロセス。
3. 赤と黒の木の左回転と右回転の複雑なプロセス。
4. Java の TreeMap は、put および deleteEntry をどのように使用して、赤黒ツリー内のノードを追加および削除しますか。
このブログ投稿を通じて、TreeMap についてより深く理解できるはずです。さて、赤黒木についての知識を簡単に広めてみましょう。
1. 赤黒ツリーの紹介
赤黒ツリーは赤黒二分木とも呼ばれ、まず第一に、二分木のすべての特性を含んでいます。木。同時に、赤黒ツリーは自己平衡型ソート二分木でもあります。
基本的なバイナリ ツリーは基本的な特性を満たす必要があることはわかっています。つまり、ツリー内の任意のノードの値がその左の子ノードよりも大きく、右の子ノードよりも小さいということです。この基本的な性質により、ツリーの検索効率が大幅に向上します。バイナリ ツリーの生成プロセスは非常に不均衡になりやすいことがわかっています。最悪のシナリオは片側 (右/左サブツリーのみ) となり、必然的にバイナリ ツリーの検索効率が大幅に低下します (O()。 n)) なので、バイナリ ツリーのバランスを維持するために、専門家は AVL、SBT、スプレッド ツリー、TREAP、赤黒ツリーなどのさまざまな実装アルゴリズムを提案しています。
バランスのとれたバイナリ ツリーは、次の特性を備えている必要があります。それは空のツリーであるか、左右のサブツリー間の高さの差の絶対値が 1 を超えず、左右のサブツリーは両方ともバランスのとれたバイナリ ツリーです。つまり、バイナリ ツリーのどのサブノードでも、その左右のサブツリーの高さは類似しています。
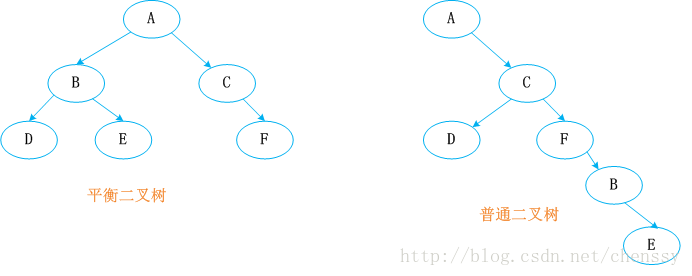
名前が示すように、赤黒ツリーは、赤または黒のノードを持つバランスの取れた二分木であり、色の制約によって二分木のバランスが維持されます。効果的な赤黒バイナリ ツリーには、次のルールを追加する必要があります:
1. 各ノードは赤または黒のみにすることができます
2。は黒です
3. 各リーフノード (NIL ノード、空ノード) は黒です。
4. ノードが赤の場合、その子ノードは両方とも黒です。つまり、隣接する 2 つの赤いノードはパス上に表示できません。 5. 任意のノードからその各リーフへのすべてのパスには、同じ数の黒いノードが含まれます。
これらの制約により、赤と黒の木の重要な性質が強制されました。根から葉までの可能な最長の経路は、可能な最短の経路ほど長くはありません。その結果、ほぼバランスのとれた木が完成します。値の挿入、削除、検索などの操作にかかる最悪の場合の時間はツリーの高さに比例する必要があるため、この理論上の高さの上限により、最悪の場合でも赤黒ツリーが効率的になることが可能になります。 、通常の二分探索木とは異なります。したがって、赤黒ツリーは複雑かつ効率的であり、その検索効率は O(logn) です。下の図は、典型的な赤黒二分木を示しています。赤と黒の二分木の場合、主に左回転、右回転、色付けという 3 つの基本操作が含まれます。
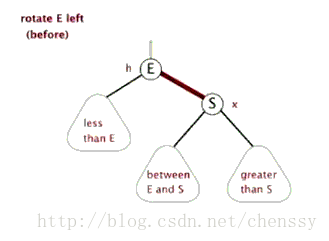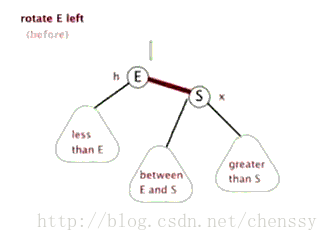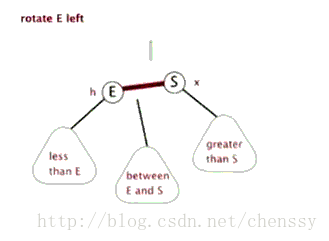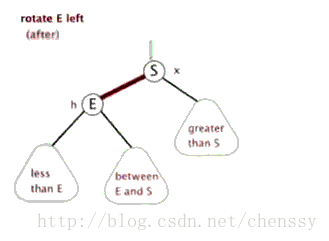
左回転
このセクションの参考文献: http://www.php.cn/Baidu Encyclopedia
注: この記事は主に Java の TreeMap について説明しているため、赤黒ツリーについてはあまり深い理解と研究がありません。より深く学びたい場合は、いくつかのより良いブログ投稿:
2、
赤黒ツリーのデータ構造の分析
3、赤と黒の木
2. TreeMapのデータ構造
> >>>>>復帰主人公: TreeMap93137b2a121d16d900ee6818f5f0da74 comparator; //TreeMap红-黑节点,为TreeMap的内部类 private transient Entryb77a8d9c3c319e50d4b02a976b347910 root = null; //容器大小 private transient int size = 0; //TreeMap修改次数 private transient int modCount = 0; //红黑树的节点颜色--红色 private static final boolean RED = false; //红黑树的节点颜色--黑色 private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子 Entryb77a8d9c3c319e50d4b02a976b347910 left = null; //右孩子 Entryb77a8d9c3c319e50d4b02a976b347910 right = null; //父亲 Entryb77a8d9c3c319e50d4b02a976b347910 parent; //颜色 boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
三、TreeMap put()方法
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树增加节点
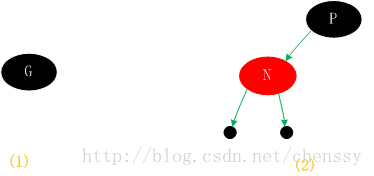
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
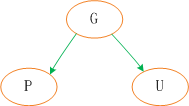
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
-
新しく挿入されたノード N に親ノードがない場合は、ノードに従って直接挿入でき、色は黒に設定されます。 (図1(1)に示すように) 2 つの黒い葉ノードになり、値は null になります。同時に、新しいノード N は赤であるため、その子ノードを通るパスには依然として同じ数の黒のノードが含まれており、これもルール 5 を満たします。 (図 1 (2) に示すように)
(図 1) この場合、直接挿入すると、間違いなくアンバランスが生じます。どうやって対処すればいいのでしょうか? P ノードと U ノードは黒に変わり、G ノードは赤に変わります。このとき、ノードP、Uを通るパスはGを経由する必要があるため、これらのパス上の黒いノードの数は変わりません。ただし、上記の処理の後、G ノードの親ノードも赤になる可能性があります。このとき、G ノードを再帰的に新しいノードとして扱う必要があります。 4. 親ノード P が赤、叔父ノード U が黒または欠落している場合、新しいノード N は P ノードの右側の子です
この場合、新しいノード N と P で左回転を実行します。ここで生成された結果は実際には完全ではなく、バランスが取れていません (ルール 4 に違反しています)。これがケース 5 で行う必要があることです。 5. 親ノード P は赤、叔父ノード U は黒または欠落しており、新しいノード N は親ノード P の左の子です

この状況は、状況 4 によって発生する場合もあれば、発生しない場合もあります。この場合、まず、P ノードを中心として右回転が行われ、回転後に生成されるツリーでは、ノード P がノード N とノード G の親ノードになります。しかし、このツリーは標準化されておらず、ルール 4 に違反しているため、仕様を満たすように P ノードと G ノードの色を交換します。最初は、すべてのパスが G を通過する必要があり、黒いノードの数は同じですが、現在はすべてのパスが P を通過し、ツリー全体で P が唯一の黒いノードであるため、調整されたツリーも仕様 5 を満たします。

上記は新しい赤と黒のツリーを示しています。これらの5つの状況はすべての新しいノードをカバーしています。いいえ赤黒ツリーがどれほど複雑であっても、これら 5 つの状況に従って生成できます。 Java の TreeMap が赤黒ツリーをどのように実装するかを分析してみましょう。TreeMap put()方法实现分析
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
-
public V put(K key, V value) { //用t表示二叉树的当前节点 Entry<K,V> t = root; //t为null表示一个空树,即TreeMap中没有任何元素,直接插入 if (t == null) { //比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序? compare(key, key); // type (and possibly null) check //将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root root = new Entry<>(key, value, null); //容器的size = 1,表示TreeMap集合中存在一个元素 size = 1; //修改次数 + 1 modCount++; return null; } int cmp; //cmp表示key排序的返回结果 Entry<K,V> parent; //父节点 // split comparator and comparable paths Comparator<? super K> cpr = comparator; //指定的排序算法 //如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合 if (cpr != null) { do { parent = t; //parent指向上次循环后的t //比较新增节点的key和当前节点key的大小 cmp = cpr.compare(key, t.key); //cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点 if (cmp < 0) t = t.left; //cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点 else if (cmp > 0) t = t.right; //cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值 else return t.setValue(value); } while (t != null); } //如果cpr为空,则采用默认的排序算法进行创建TreeMap集合 else { if (key == null) //key值为空抛出异常 throw new NullPointerException(); /* 下面处理过程和上面一样 */ Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } //将新增节点当做parent的子节点 Entry<K,V> e = new Entry<>(key, value, parent); //如果新增节点的key小于parent的key,则当做左子节点 if (cmp < 0) parent.left = e; //如果新增节点的key大于parent的key,则当做右子节点 else parent.right = e; /* * 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置 * 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况 */ fixAfterInsertion(e); //TreeMap元素数量 + 1 size++; //TreeMap容器修改次数 + 1 modCount++; return null; } 上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
-
/** * 新增节点后的修复操作 * x 表示新增节点 */ private void fixAfterInsertion(Entry<K,V> x) { x.color = RED; //新增节点的颜色为红色 //循环 直到 x不是根节点,且x的父节点不为红色 while (x != null && x != root && x.parent.color == RED) { //如果X的父节点(P)是其父节点的父节点(G)的左节点 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { //获取X的叔节点(U) Entry<K,V> y = rightOf(parentOf(parentOf(x))); //如果X的叔节点(U) 为红色(情况三) if (colorOf(y) == RED) { //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的叔节点(U)设置为黑色 setColor(y, BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } //如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五) else { //如果X节点为其父节点(P)的右子树,则进行左旋转(情况四) if (x == rightOf(parentOf(x))) { //将X的父节点作为X x = parentOf(x); //右旋转 rotateLeft(x); } //(情况五) //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); //以X的父节点的父节点(G)为中心右旋转 rotateRight(parentOf(parentOf(x))); } } //如果X的父节点(P)是其父节点的父节点(G)的右节点 else { //获取X的叔节点(U) Entry<K,V> y = leftOf(parentOf(parentOf(x))); //如果X的叔节点(U) 为红色(情况三) if (colorOf(y) == RED) { //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的叔节点(U)设置为黑色 setColor(y, BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } //如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五) else { //如果X节点为其父节点(P)的右子树,则进行左旋转(情况四) if (x == leftOf(parentOf(x))) { //将X的父节点作为X x = parentOf(x); //右旋转 rotateRight(x); } //(情况五) //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); //以X的父节点的父节点(G)为中心右旋转 rotateLeft(parentOf(parentOf(x))); } } } //将根节点G强制设置为黑色 root.color = BLACK; } -
对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
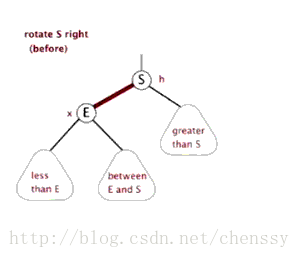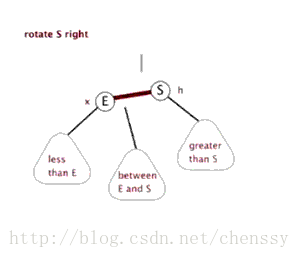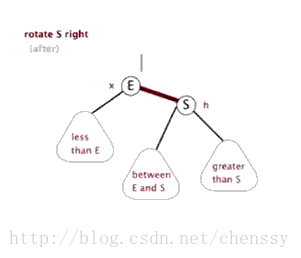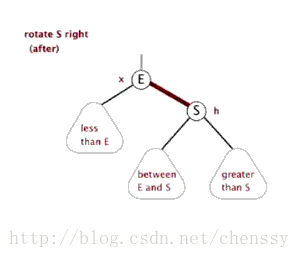
右旋:rotateRight()
对于排序二叉树的创建,其添加节点的过程如下:
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
}所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}左旋、右旋的示意图如下:

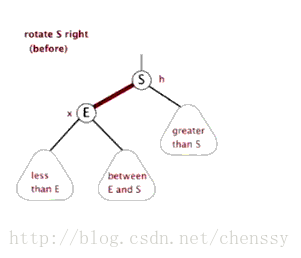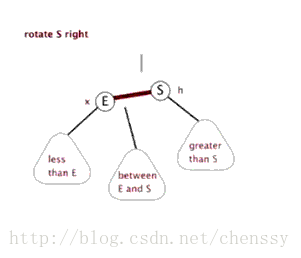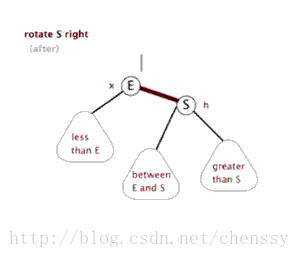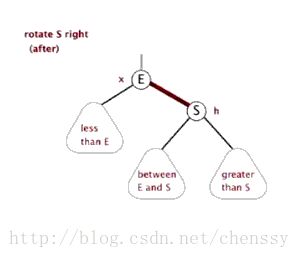
(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}四、TreeMap delete()方法
红黑树删除节点
针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。
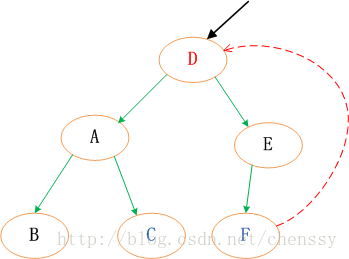
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1. 各ノードは赤または黒のみです
2. ルートノードは黒です
3. 各リーフノード (NIL ノード、空ノード) は黒色です。
4. ノードが赤の場合、その子ノードは両方とも黒です。つまり、隣接する 2 つの赤いノードはパス上に表示できません。 5. 任意のノードからその各リーフへのすべてのパスには、同じ数の黒いノードが含まれます。
(注:3回言いました。覚えていない方はITに向いているかどうか疑ってしまいますO(∩_∩)O~)
確かにノードの削除はより複雑であるため、ここでのルールに同意しましょう:
1. 以下で説明する削除されたノードは、前述したように、削除される実際のノードの後継ノード (N) C.
2. 以下で説明するノードを削除するツリーは次の構造を持っています。この構造で選択されるノードは、削除されるノードの右のツリーの一番左の子ノードです。ここで、実際に削除されたノードを N、親ノードを P、兄弟ノードを W、兄弟ノードの 2 つの子ノードを X1 と X2 とします。以下に示すように (2.1)。
次に、上記の 3 つの状況の処理を分析します。 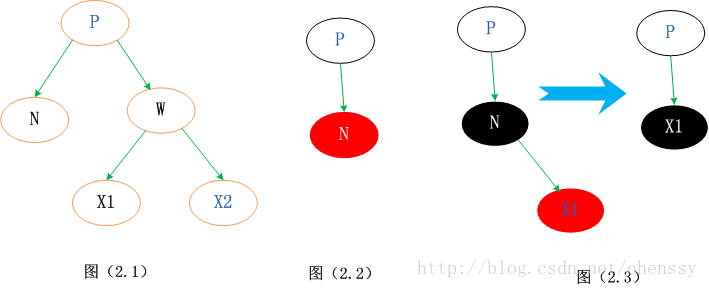
状況 1. 子ノードがない (赤いノード)
この場合、ノードは影響ツリー構造を使用せずに直接削除できます。ノードはリーフ ノードであるため、子ノードを持つことはできません。子ノードが黒の場合は黒ノードの数の原則 (第 5 条) に違反し、赤の場合は「」に違反します。 「カラー」原則(第4条)。 上図 (2.2) に示すとおりです。
状況 2: 子ノードがある
この状況も、ノードを削除してから子ノードを削除するだけです。上の図に示すように (2.3)
ケース 3. 2 つの子ノードがあります
この状況は少し複雑かもしれません。削除する代替ノード (N) を見つけて置き換えてから、N を削除する必要があります。それは主に4つの状況に分けられます。 1. N の兄弟ノード W は赤です 2. N の兄弟 W は黒で、W の子供は両方とも黒です。 3. N の弟 w は黒人、w の左の子は赤、w の右の子は黒です。 4. N の兄弟 w は黒人で、w の右の子供は赤人です。 " W が赤の場合、その子ノード X1 と X2 はすべて黒でなければなりません。親ノード P も黒です。処理戦略は、W と P の色を変更してから左回転を実行することです。この処理により、赤と黒の特性を維持し続けることができます。 N の新しい兄弟、新しい w は、ローテーション前の w の子供で、黒人です。この処理の後、状況 3.1 は 3.2、3.3、および 3.4 のいずれかに変換されます。以下の通り: ケース 3.2. N の兄弟 w は黒人で、w の子供は 2 人とも黒人です。 この場合、W は黒であるため、N サブツリーの黒ノードは兄弟の W サブツリーよりも 1 つ少なくなります。 Wは赤に設定可能です。このようにして、N サブツリーと W サブツリーの黒いノードは一致し、バランスが保たれます。次のように 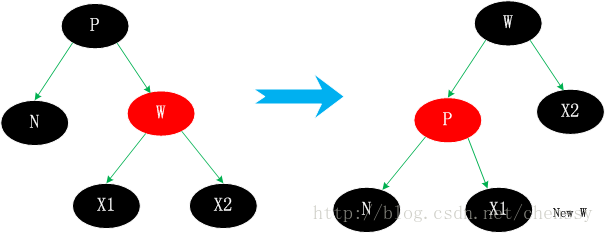
これにより、新しいノード new N がその兄弟ノードに対して相対的になります。黒ノード。ただし、新しい x が赤の場合は、ツリー全体のバランスを維持するために、新しい x を直接黒に変換します。それ以外の場合、状況 3.2 は状況 3.1、3.3、および 3.4 のいずれかに変化します。

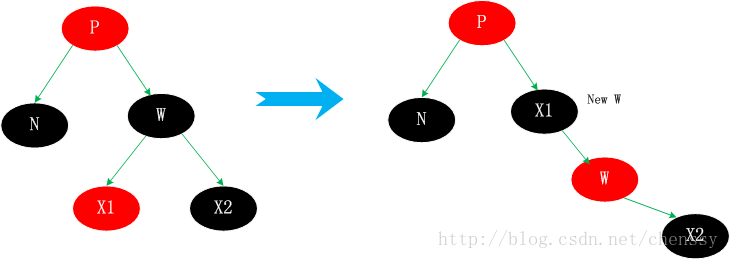
この場合、ノード W とその左の子ノードの色を交換し、W を右回転します。
Wと親ノードPの色を交換し、同時にPに対して左回転操作を行います。これにより、左側に欠けている黒いノードが埋められます。同時に、W の右側の子ノード X2 を黒に設定します。このようにして、左右のバランスが保たれます。
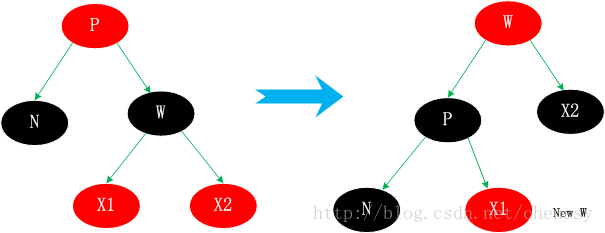
总结
个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。
通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。
TreeMap deleteEntry()方法实现分析
通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}(1)除是寻找替代节点replacement,其实现方法为successor()。如下:
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}(2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下:
1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。
private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
} 这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。
5. 最後に書きました
このブログ記事は確かに少し長いですが、読んでいただきありがとうございます 落ち着いていただければ最後までお読みください。このブログ投稿を読んで多くのことを学んでいただければ幸いです。同時に、このブログ投稿では赤黒ツリーの実装プロセスの説明に多くのスペースを割いており、Java の TreeMap についてはあまり触れていません。ただし、赤黒ツリーの実装プロセスを理解していれば理解できると思います。 TreeMap を簡単にマスターできます。
同時に、このブログ記事を4日間書き、たくさんのブログ記事を読んで参考にさせていただきました。同時に、参考になる点も必ずあると思いますので、感謝を申し上げたいと思います。 LZ は 2 年生からデータ構造を学び始めました。私はよくやったと思いましたが、同時にデータ構造について学ぶことが多すぎると感じました。 ! !
上記は Java 改善章 (27) -----TreeMap の内容です。その他の関連コンテンツについては、PHP 中国語 Web サイト (www.php.cn) に注目してください。