一般的に使用される検索データ構造とアルゴリズムの詳細な説明 (Python 実装)

1. 基本概念

検索とは、指定された値に基づいて、ルックアップ テーブル内の指定された値とキーが等しいデータ要素 (またはレコード) を決定することです。

検索テーブル: 同じタイプのデータ要素 (またはレコード) のコレクション

キー: データ要素内のデータ項目の値。キー値とも呼ばれます。

主キー: データ要素またはレコードを一意に識別するキーワード。

ルックアップ テーブルは次のように分類できます。

静的検索テーブル: 検索操作のみを実行するルックアップ テーブル。その主な操作は次のとおりです:

「特定の」データ要素がテーブル内にあるかどうかをクエリします

「特定の」データ要素とさまざまな属性を取得します

動的検索テーブル: 検索中に挿入や削除などの操作を同時に実行します:

検索中にデータを挿入

検索中にデータを削除

2. 順序なしテーブル検索

は、データを並べ替えずにデータ要素を横断する線形検索です。

アルゴリズム分析: 最良の場合は最初の位置 (O(1)) で検出され、最悪の場合は最後の位置 (O(n)) で検出されます。検索数は (n +1)/2 です。最終的な時間計算量は O(n)

# 最基础的遍历无序列表的查找算法
# 时间复杂度O(n)
 
def sequential_search(lis, key):
  length = len(lis)
  for i in range(length):
    if lis[i] == key:
      return i
    else:
      return False
 
 
if __name__ == '__main__':
  LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
  result = sequential_search(LIST, 123)
  print(result)

3. 順序付きテーブル検索

ルックアップ テーブル内のデータは主キーに従って並べ替える必要があります。

1. 二分探索

アルゴリズムの核心: ルックアップ テーブル内の中間要素とルックアップ値を継続的に比較し、テーブル範囲を半分に縮小します。

# 针对有序查找表的二分查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    mid = int((low + high) / 2)
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印折半的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 99)
  print(result)

2. 補間探索

二分探索法はすでに非常に優れていますが、最適化できる領域がまだあります。

場合によっては、半分にフィルタリングするだけでは不十分な場合があります。毎回、データの 10 分の 9 を除外した方がよいのではありませんか。この値の選択が重要な問題です。補間の意味は、より高速に縮小することです。

補間の中核は次の式を使用することです:

value = (key - list[low])/(list[high] - list[low])

この値を使用してバイナリの 1/2 を置き換えます検索。

上記のコードは直接使用でき、1 文を変更するだけで済みます。

# 插值查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    # 计算mid值是插值算法的核心代码
    mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low]))
    print("mid=%s, low=%s, high=%s" % (mid, low, high))
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印查找的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 444)
  print(result)

内挿アルゴリズムの全体的な時間計算量は依然として O(log(n)) レベルです。利点は、テーブル内に大量のデータがあり、キーワードが比較的均等に分散されているルックアップ テーブルの場合、内挿アルゴリズムを使用した平均パフォーマンスがバイナリ検索よりもはるかに優れていることです。逆に、分布が極端に不均一なデータの場合は、補間アルゴリズムは適しません。

3. フィボナッチ検索

補間アルゴリズムに触発されて、フィボナッチ アルゴリズムが発明されました。検索回数を最小限に抑えるために、削減率をいかに最適化するかということも核心となります。

フィボナッチデータを含むリストが既にあると仮定してこのアルゴリズムを使用します

F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ,...]

# 斐波那契查找算法
# 时间复杂度O(log(n))
 
def fibonacci_search(lis, key):
  # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。
  F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
     233, 377, 610, 987, 1597, 2584, 4181, 6765,
     10946, 17711, 28657, 46368]
  low = 0
  high = len(lis) - 1
   
  # 为了使得查找表满足斐波那契特性，在表的最后添加几个同样的值
  # 这个值是原查找表的最后那个元素的值
  # 添加的个数由F[k]-1-high决定
  k = 0
  while high > F[k]-1:
    k += 1
  print(k)
  i = high
  while F[k]-1 > i:
    lis.append(lis[high])
    i += 1
  print(lis)
   
  # 算法主逻辑。time用于展示循环的次数。
  time = 0
  while low <= high:
    time += 1
    # 为了防止F列表下标溢出，设置if和else
    if k < 2:
      mid = low
    else:
      mid = low + F[k-1]-1
     
    print("low=%s, mid=%s, high=%s" % (low, mid, high))
    if key < lis[mid]:
      high = mid - 1
      k -= 1
    elif key > lis[mid]:
      low = mid + 1
      k -= 2
    else:
      if mid <= high:
        # 打印查找的次数
        print("times: %s" % time)
        return mid
      else:
        print("times: %s" % time)
        return high
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = fibonacci_search(LIST, 444)
  print(result)

アルゴリズム分析: フィボナッチ検索の全体的な時間計算量も O(log(n)) です。ただし、平均パフォーマンスの観点からは、二分探索よりも優れています。ただし、最悪の場合、例えばキーが1の場合、常に左半分の領域を探索することになり、二分探索よりも効率が悪くなります。

要約: 二分探索の中間演算は加算と除算であり、補間探索は複雑な四則演算であり、フィボナッチ探索は最も単純な加算と減算にすぎません。大量のデータを検索する場合、この微妙な違いが最終的な検索効率に影響を与える可能性があります。したがって、順序付けされたテーブルの 3 つの検索方法は、分割ポイントの選択において本質的に異なります。それぞれに独自の長所と短所があり、実際の状況に基づいて選択する必要があります。

4. 線形インデックス検索

大量の順序付けされていないデータの場合、検索速度を向上させるために、一般にインデックス テーブルが構築されます。

インデックス作成は、キーワードを対応するレコードに関連付けるプロセスです。

インデックスは複数のインデックス項目で構成され、各インデックス項目には少なくともキーワードやメモリ内の対応するレコードの位置などの情報が含まれます。

インデックスは、その構造に応じて、線形インデックス、ツリーインデックス、マルチレベルインデックスに分類できます。

線形インデックス: 線形構造 (インデックス テーブルとも呼ばれる) を通じてインデックス項目のコレクションを整理します。

線形インデックスは、密インデックス、ブロックインデックス、転置インデックスに分類できます

1. 密インデックス

密インデックスとは、線形インデックス項目内のデータセット内の各レコードのインデックスの確立を指します。

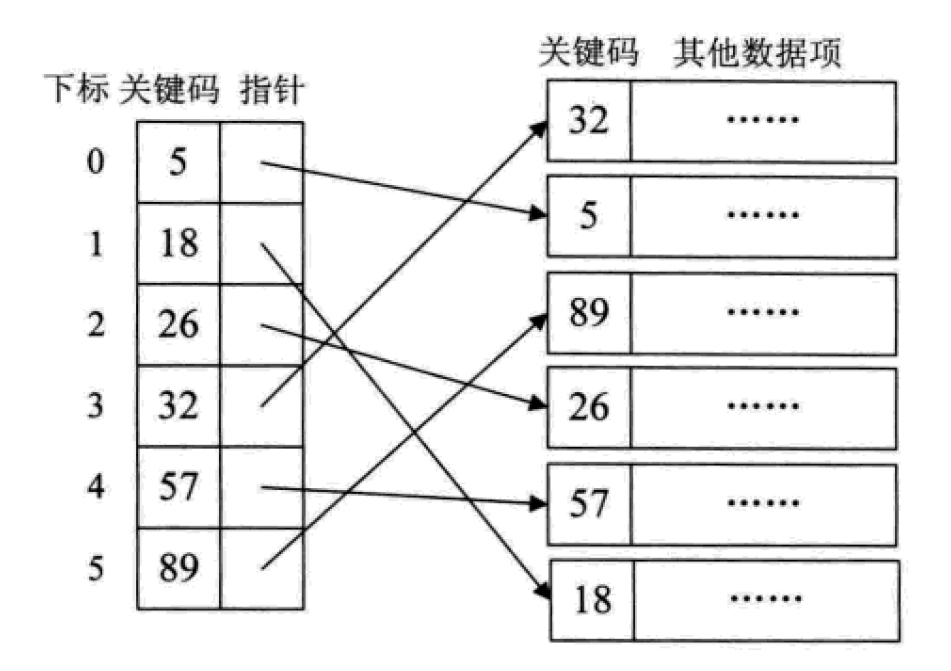
これは実際には、順序なし集合に対して順序付き線形テーブルを構築するのと同じです。インデックス項目はキーコードに応じた順序で配置する必要があります。

これも、検索処理で必要となる仕分け作業を事前に行っておくことに相当します。

1. ブロックインデックス

は、多数の順序付けされていないデータセットをブロックに分割し、ブロック内に無秩序性とブロック間に順序性を持たせます。

这其实是有序查找和无序查找的一种中间状态或者说妥协状态。因为数据量过大，建立完整的稠密索引耗时耗力，占用资源过多；但如果不做任何排序或者索引，那么遍历的查找也无法接受，只能折中，做一定程度的排序或索引。

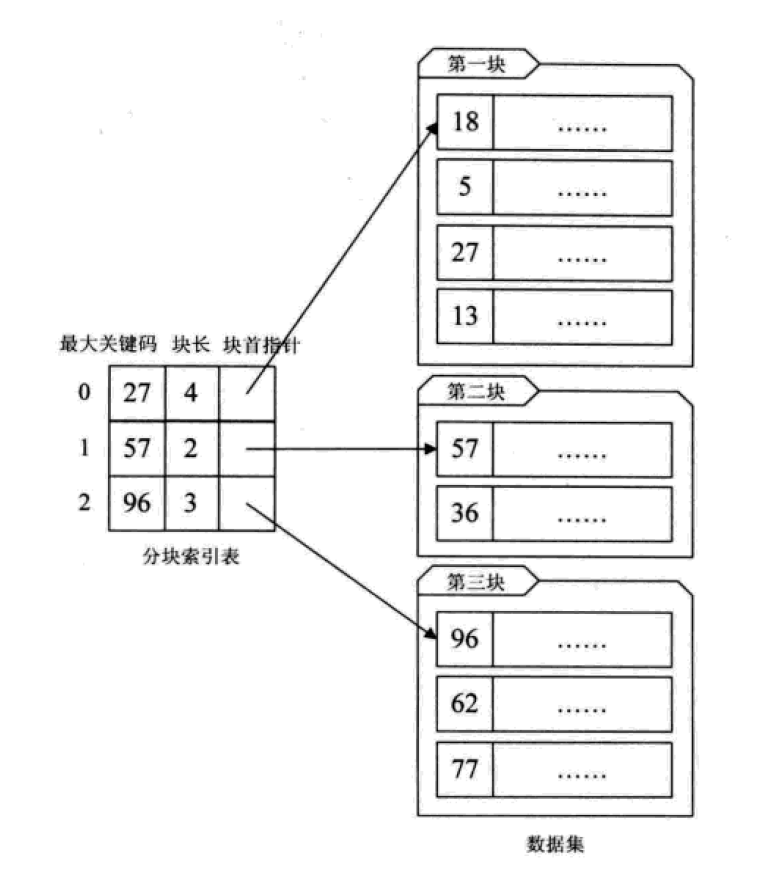
分块索引的效率比遍历查找的O(n)要高一些，但与二分查找的O(logn)还是要差不少。

1.倒排索引

不是由记录来确定属性值，而是由属性值来确定记录的位置，这种被称为倒排索引。其中记录号表存储具有相同次关键字的所有记录的地址或引用（可以是指向记录的指针或该记录的主关键字）。

倒排索引是最基础的搜索引擎索引技术。

五、二叉排序树

二叉排序树又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值均小于它的根结构的值；

若它的右子树不为空，则右子树上所有节点的值均大于它的根结构的值；

它的左、右子树也分别为二叉排序树。

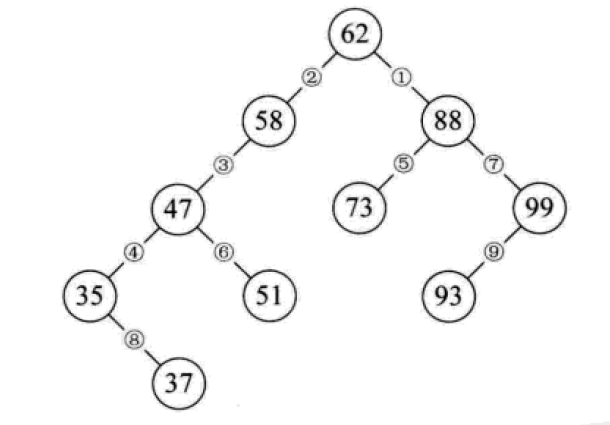
构造一颗二叉排序树的目的，往往不是为了排序，而是为了提高查找和插入删除关键字的速度。

二叉排序树的操作：

1.查找：对比节点的值和关键字，相等则表明找到了；小了则往节点的左子树去找，大了则往右子树去找，这么递归下去，最后返回布尔值或找到的节点。

2.插入：从根节点开始逐个与关键字进行对比，小了去左边，大了去右边，碰到子树为空的情况就将新的节点链接。

3.删除：如果要删除的节点是叶子，直接删；如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；如果同时有左右子树，则可以将二叉排序树进行中序遍历，取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
 
 
class BSTNode:
  """
  定义一个二叉树节点类。
  以讨论算法为主，忽略了一些诸如对数据类型进行判断的问题。
  """
  def __init__(self, data, left=None, right=None):
    """
    初始化
    :param data: 节点储存的数据
    :param left: 节点左子树
    :param right: 节点右子树
    """
    self.data = data
    self.left = left
    self.right = right
 
 
class BinarySortTree:
  """
  基于BSTNode类的二叉排序树。维护一个根节点的指针。
  """
  def __init__(self):
    self._root = None
 
  def is_empty(self):
    return self._root is None
 
  def search(self, key):
    """
    关键码检索
    :param key: 关键码
    :return: 查询节点或None
    """
    bt = self._root
    while bt:
      entry = bt.data
      if key < entry:
        bt = bt.left
      elif key > entry:
        bt = bt.right
      else:
        return entry
    return None
 
  def insert(self, key):
    """
    插入操作
    :param key:关键码
    :return: 布尔值
    """
    bt = self._root
    if not bt:
      self._root = BSTNode(key)
      return
    while True:
      entry = bt.data
      if key < entry:
        if bt.left is None:
          bt.left = BSTNode(key)
          return
        bt = bt.left
      elif key > entry:
        if bt.right is None:
          bt.right = BSTNode(key)
          return
        bt = bt.right
      else:
        bt.data = key
        return
 
  def delete(self, key):
    """
    二叉排序树最复杂的方法
    :param key: 关键码
    :return: 布尔值
    """
    p, q = None, self._root   # 维持p为q的父节点，用于后面的链接操作
    if not q:
      print("空树！")
      return
    while q and q.data != key:
      p = q
      if key < q.data:
        q = q.left
      else:
        q = q.right
      if not q:        # 当树中没有关键码key时，结束退出。
        return
    # 上面已将找到了要删除的节点，用q引用。而p则是q的父节点或者None（q为根节点时）。
    if not q.left:
      if p is None:
        self._root = q.right
      elif q is p.left:
        p.left = q.right
      else:
        p.right = q.right
      return
    # 查找节点q的左子树的最右节点，将q的右子树链接为该节点的右子树
    # 该方法可能会增大树的深度，效率并不算高。可以设计其它的方法。
    r = q.left
    while r.right:
      r = r.right
    r.right = q.right
    if p is None:
      self._root = q.left
    elif p.left is q:
      p.left = q.left
    else:
      p.right = q.left
 
  def __iter__(self):
    """
    实现二叉树的中序遍历算法,
    展示我们创建的二叉排序树.
    直接使用python内置的列表作为一个栈。
    :return: data
    """
    stack = []
    node = self._root
    while node or stack:
      while node:
        stack.append(node)
        node = node.left
      node = stack.pop()
      yield node.data
      node = node.right
 
 
if __name__ == &#39;__main__&#39;:
  lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
  bs_tree = BinarySortTree()
  for i in range(len(lis)):
    bs_tree.insert(lis[i])
  # bs_tree.insert(100)
  bs_tree.delete(58)
  for i in bs_tree:
    print(i, end=" ")
  # print("\n", bs_tree.search(4))

   

二叉排序树总结：

二叉排序树以链式进行存储，保持了链接结构在插入和删除操作上的优点。

在极端情况下，查询次数为1，但最大操作次数不会超过树的深度。也就是说，二叉排序树的查找性能取决于二叉排序树的形状，也就引申出了后面的平衡二叉树。

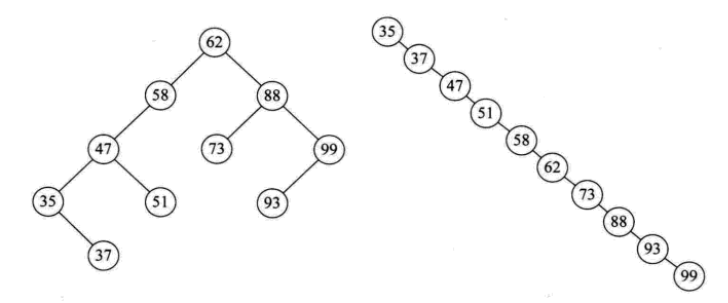
给定一个元素集合，可以构造不同的二叉排序树，当它同时是一个完全二叉树的时候，查找的时间复杂度为O(log(n))，近似于二分查找。

当出现最极端的斜树时，其时间复杂度为O(n)，等同于顺序查找，效果最差。

六、 平衡二叉树

平衡二叉树（AVL树，发明者的姓名缩写）：一种高度平衡的排序二叉树，其每一个节点的左子树和右子树的高度差最多等于1。

平衡二叉树首先必须是一棵二叉排序树！

平衡因子（Balance Factor）：将二叉树上节点的左子树深度减去右子树深度的值。

对于平衡二叉树所有包括分支节点和叶节点的平衡因子只可能是-1,0和1，只要有一个节点的因子不在这三个值之内，该二叉树就是不平衡的。

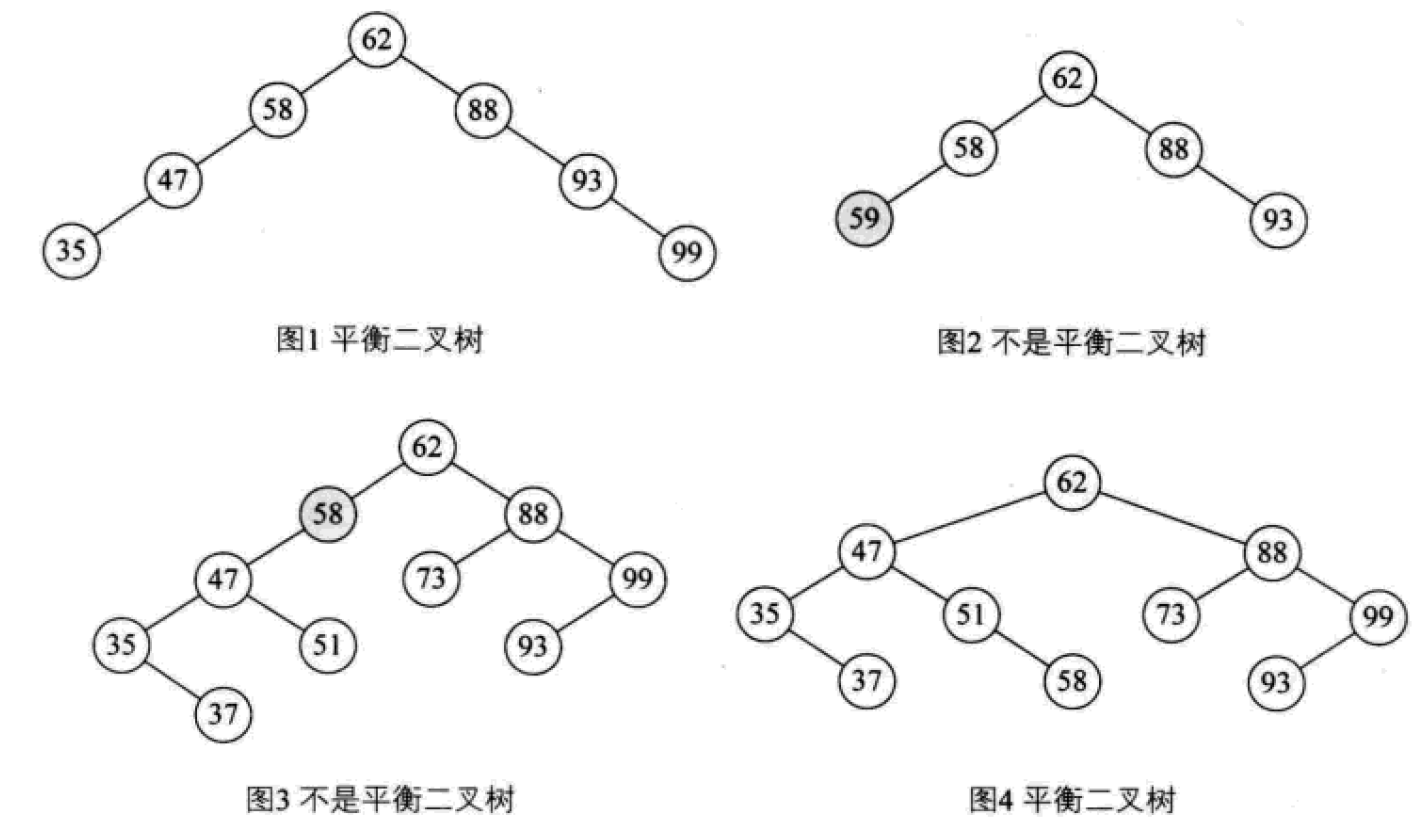
最小不平衡子树：距离插入结点最近的，且平衡因子的绝对值大于1的节点为根的子树。

平衡二叉树的构建思想：每当插入一个新结点时，先检查是否破坏了树的平衡性，若有，找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的连接关系，进行相应的旋转，成为新的平衡子树。

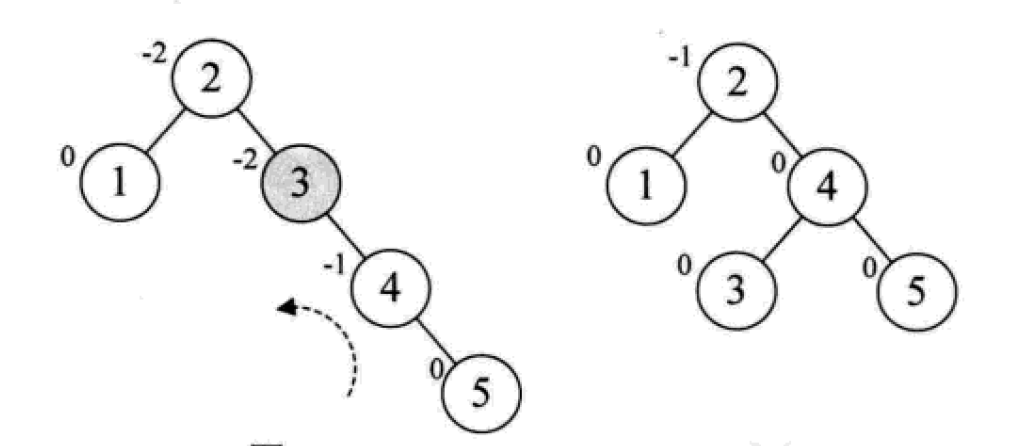
下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树

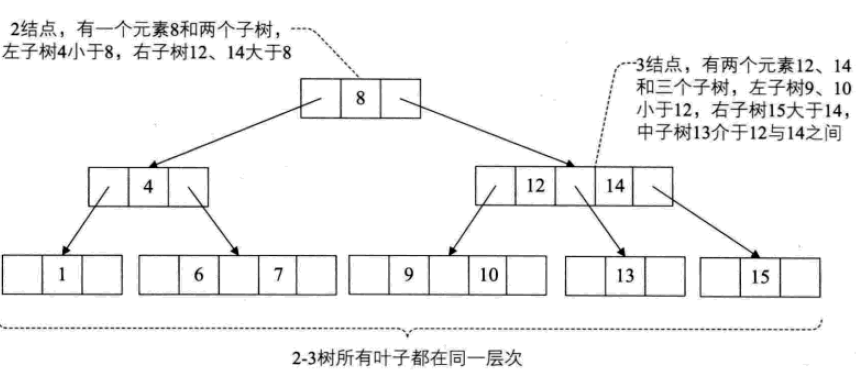
7. 多方向検索ツリー (B ツリー): 各ノードは 2 つ以上の子を持つことができ、各ノードは格納できます。複数の要素。

マルチウェイ検索ツリーの場合、各ノードが格納できる要素の数とその子の数が重要です。一般的に使用される形式は 2-3 ツリー、2-3-4 ツリー、B ツリー、および B+ ツリーの 4 つです。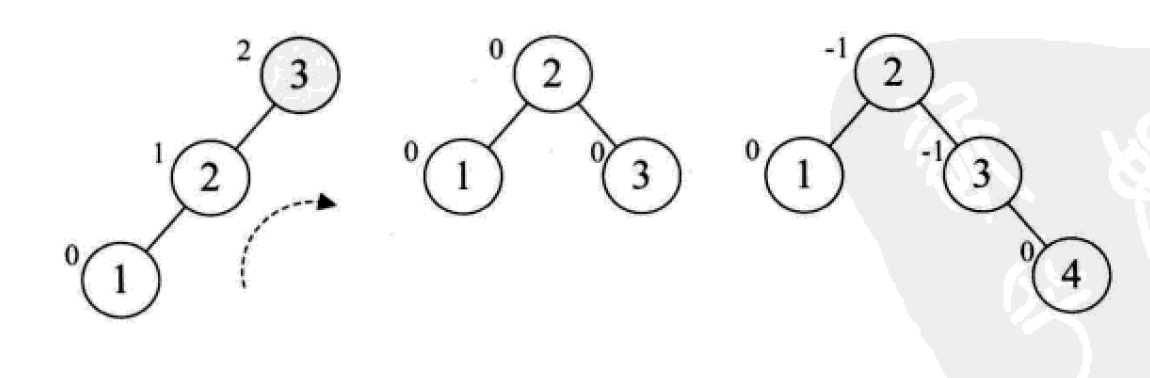

2-3 ツリー

2-3 ツリー: 各ノードには 2 つの子、3 つの子、または子がありません。

2 ノードには 1 つの要素と 2 つの子が含まれます (または子が存在せず、子を 1 つだけ持つことはできません)。バイナリソートツリーと同様に、左側のサブツリーに含まれる要素はすべてその要素より小さく、右側のサブツリーに含まれる要素はその要素より大きくなります。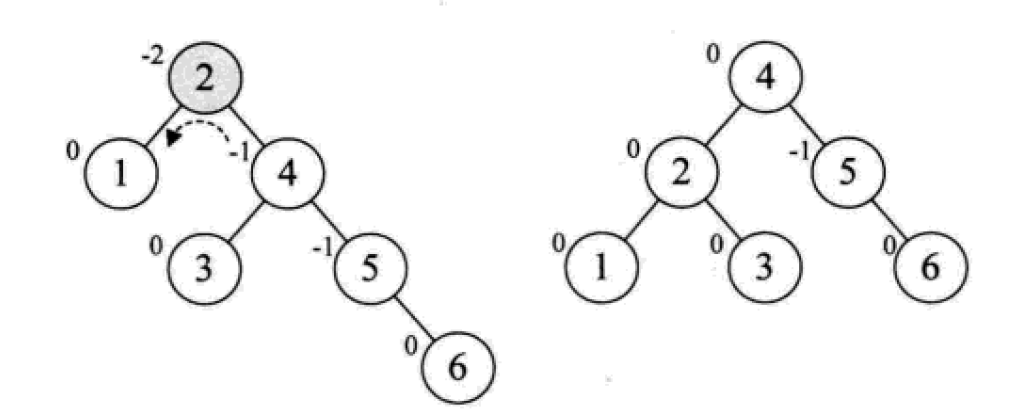

3 ノードには、2 つの要素と 3 つの子 (または、1 つまたは 2 つの子だけではなく、子がありません) が含まれます。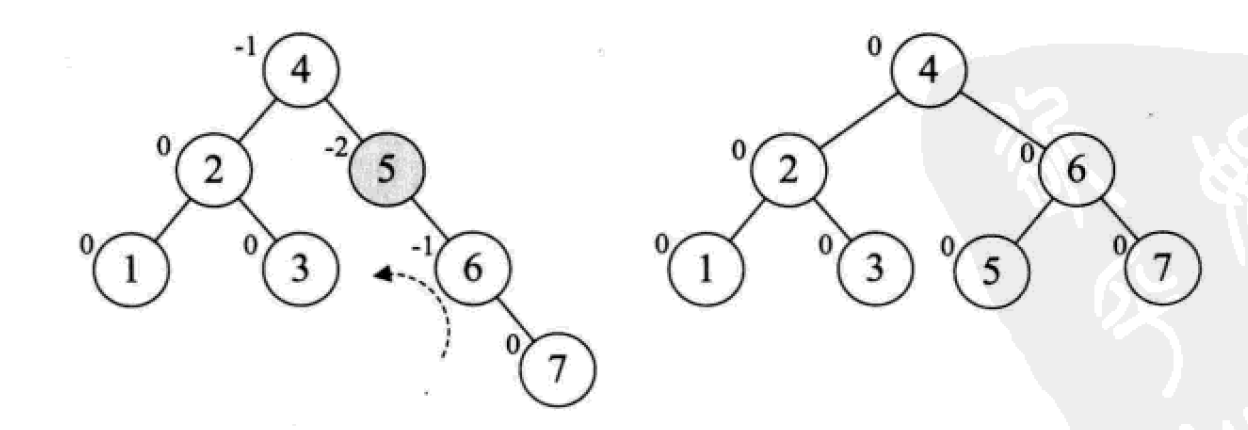

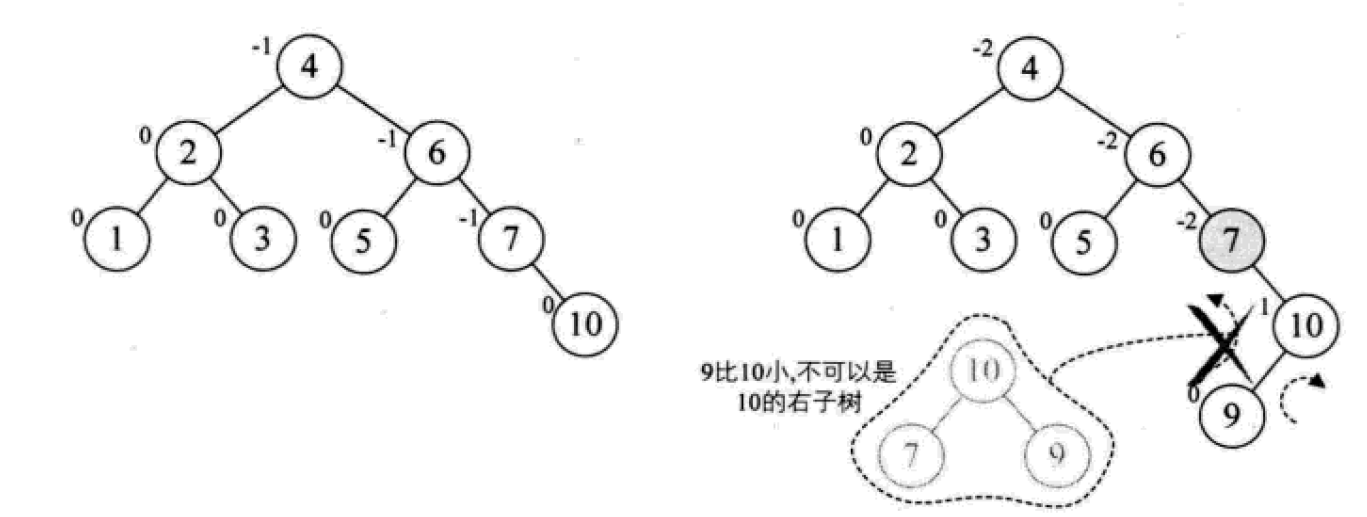
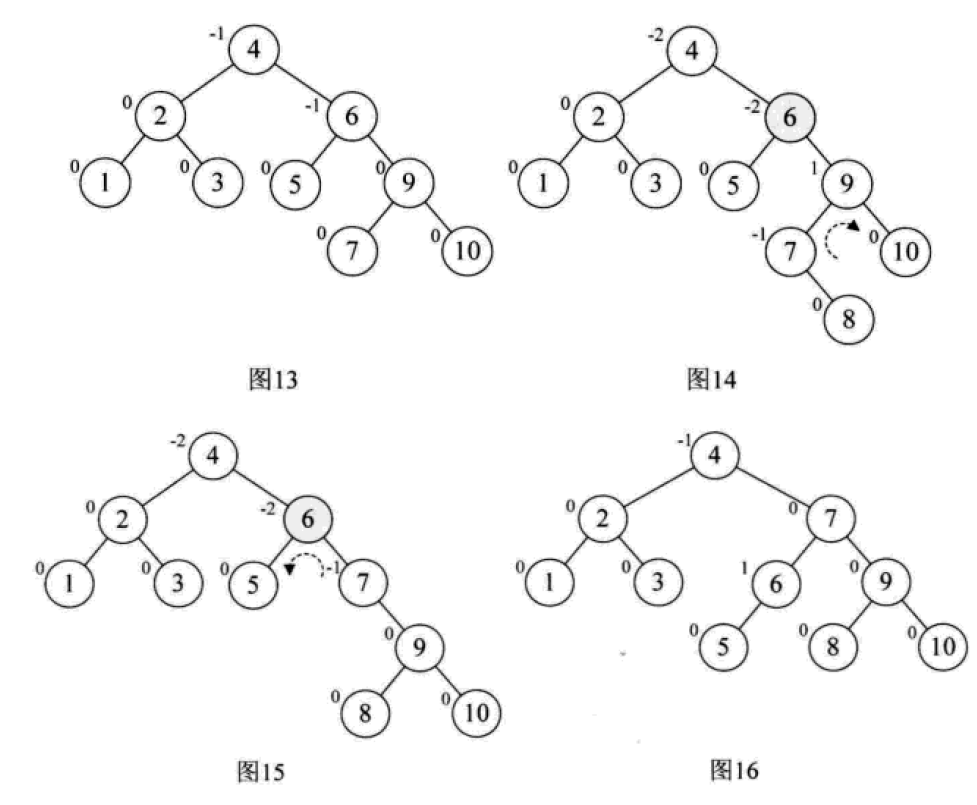
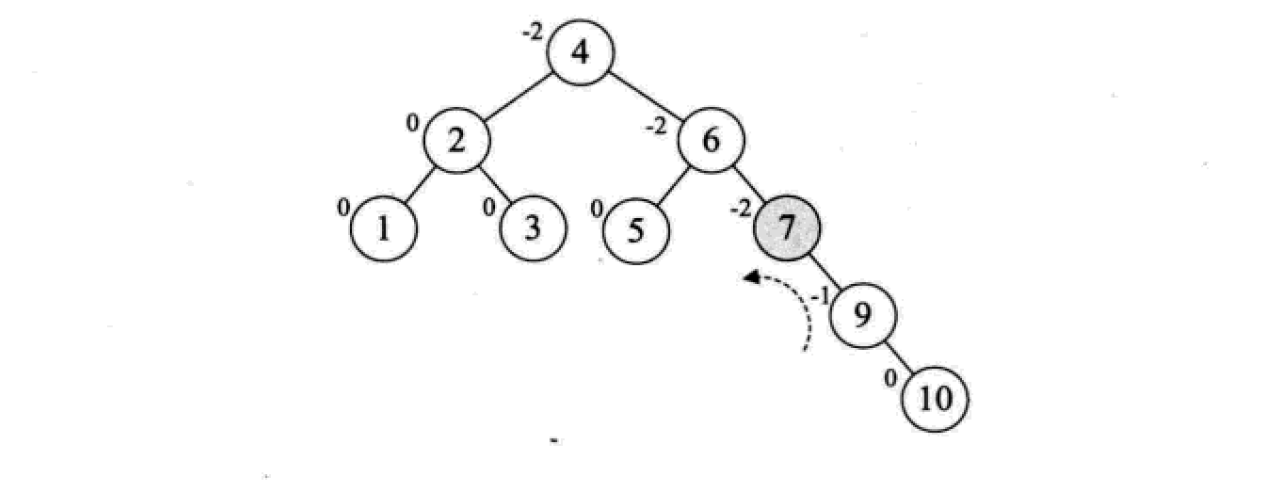2-3 ツリー内のすべての葉は同じレベルにある必要があります。

挿入操作は次のとおりです。

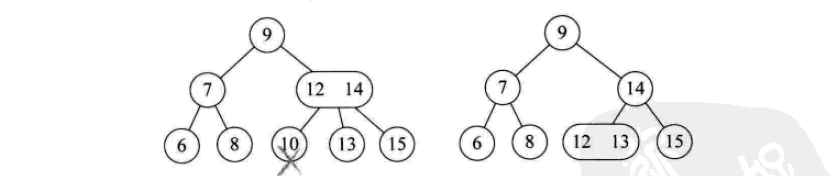
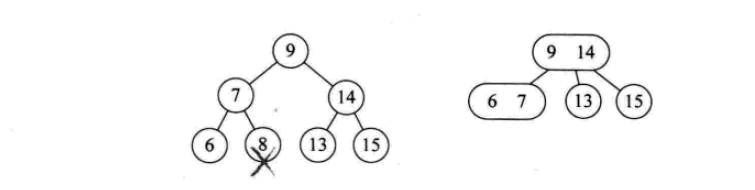
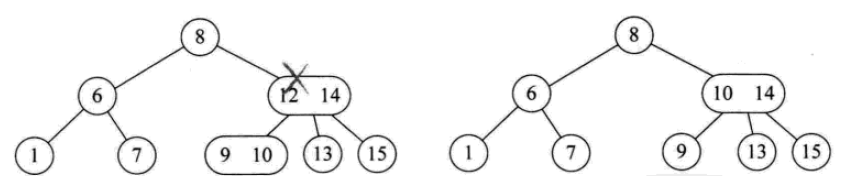
削除操作は次のとおりです。

2-3-4ツリー

は、実際には、4つのノードの使用を含む、2-3ツリーの拡張です。 4 ノードには、小、中、大の 3 つの要素と 4 つの子 (または子なし) が含まれます。

その挿入操作:

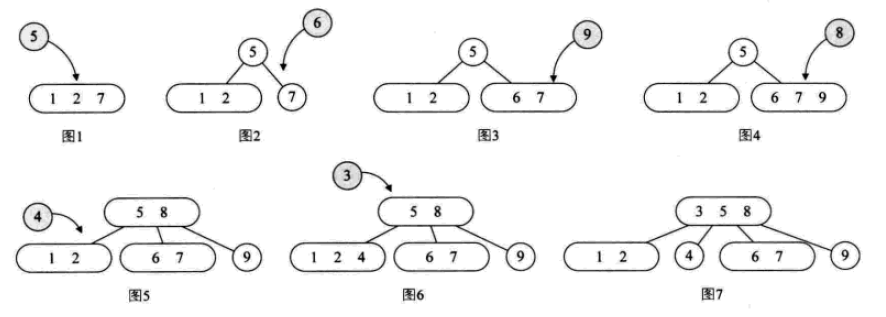
その削除操作:

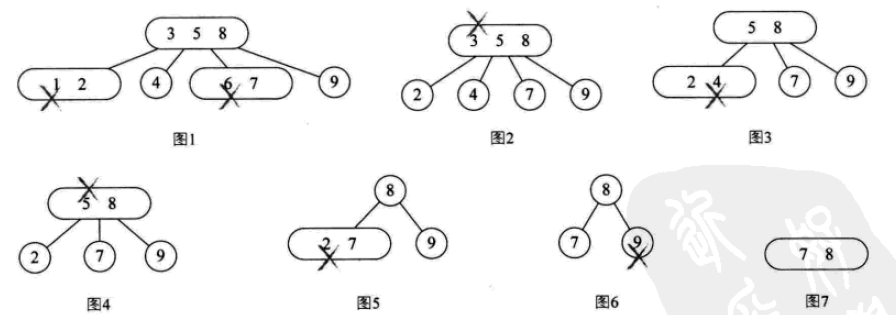
B ツリー

B ツリーは平衡型多方向探索ツリーです。ノードの子の最大数は、B ツリーの次数と呼ばれます。 2-3 ツリーは 3 次の B ツリー、2-3-4 は 4 次の B ツリーです。

Bツリーのデータ構造は、主にメモリと外部メモリ間のデータ相互作用に使用されます。

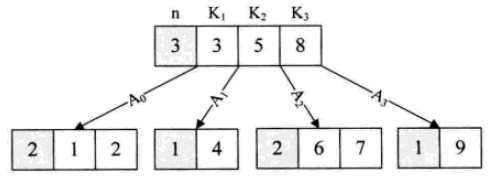
B+ツリー

Bツリーのすべての要素を走査するという基本的な問題を解決するために、B+ツリーは元の構造に基づいて形成され、新しい要素構成方法が追加されました。

B+ツリーは、ファイルシステムのニーズに応じて出現したBツリーの変形ツリーであり、もはや最も基本的なツリーではありません。

B+ ツリーでは、ブランチ ノードに出現する要素は、そのブランチ ノードの位置にある順序の後続ノード (葉ノード) として再度リストされます。さらに、各リーフ ノードは次のリーフ ノードへのポインタを保存します。

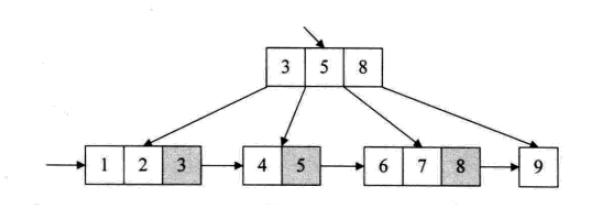
すべてのリーフノードには、すべてのキーワード情報と関連するポインターが含まれています。リーフノード自体は、キーワードのサイズに従って昇順にリンクされています

B+ ツリーの構造は、範囲を使用した検索に特に適しています。たとえば、20 歳から 30 歳までの人を検索します。

8. ハッシュテーブル (ハッシュテーブル)

ハッシュテーブル: すべての要素間に関係はありません。要素の格納場所は、要素のキーワードを使用して関数を通じて直接計算されます。この 1 対 1 の関係関数をハッシュ関数またはハッシュ関数と呼びます。

ハッシュ技術を使用して、ハッシュテーブルまたはハッシュテーブル（ハッシュテーブル）と呼ばれる連続的なストレージスペースにレコードを保存します。キーワードに対応する格納場所をハッシュアドレスと呼びます。

ハッシュ テーブルは検索指向のストレージ構造です。これが最も適している問題は、指定された値に等しいレコードを見つけることです。ただし、性別「男性」をすべて検索するなど、特定のキーワードが多数のレコードに対応する可能性がある状況には適していません。また、20代から30代までの範囲での検索にも適していません。並べ替え、最大値、最小値なども不適切です。

したがって、ハッシュ テーブルは通常、キーワードが繰り返されないデータ構造に使用されます。たとえば、Python の辞書データ型です。

シンプルで均一、ストレージ使用率の高いハッシュ関数を設計することは、ハッシュ テクノロジにおいて最も重要な問題です。

ただし、一般的なハッシュ関数は競合の問題に直面します。

競合: 2 つの異なるキーワードがハッシュ関数によって計算された後、同じ結果になります。衝突。

8.1 ハッシュ関数の構築方法

良いハッシュ関数: 単純な計算、ハッシュアドレスの均等な分散

1. 直接アドレス指定方法

たとえば、キーワードの一次関数をハッシュ関数としてとります:

f(key) = a*key + b (a、bは定数)

2.数字分析法

 抽取关键字里的数字，根据数字的特点进行地址分配

3.平方取中法 

将关键字的数字求平方，再截取部分

4.折叠法

 将关键字的数字分割后分别计算，再合并计算，一种玩弄数字的手段。

5.除留余数法

 最为常见的方法之一。

 对于表长为m的数据集合，散列公式为：

f(key) = key mod p (p

 mod：取模（求余数）

 该方法最关键的是p的选择，而且数据量较大的时候，冲突是必然的。一般会选择接近m的质数。

6.随机数法

 选择一个随机数，取关键字的随机函数值为它的散列地址。

f(key) = random(key)

总结，实际情况下根据不同的数据特性采用不同的散列方法，考虑下面一些主要问题：

计算散列地址所需的时间

关键字的长度

散列表的大小

关键字的分布情况

记录查找的频率

8.2 处理散列冲突

1、开放定址法

就是一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

公式是：

这种简单的冲突解决办法被称为线性探测，无非就是自家的坑被占了，就逐个拜访后面的坑，有空的就进，也不管这个坑是不是后面有人预定了的。

 线性探测带来的最大问题就是冲突的堆积，你把别人预定的坑占了，别人也就要像你一样去找坑。

改进的办法有二次方探测法和随机数探测法。

2、再散列函数法

发生冲突时就换一个散列函数计算，总会有一个可以把冲突解决掉，它能够使得关键字不产生聚集，但相应地增加了计算的时间。

3、链接地址法
 碰到冲突时，不更换地址，而是将所有关键字为同义词的记录存储在一个链表里，在散列表中只存储同义词子表的头指针，如下图：

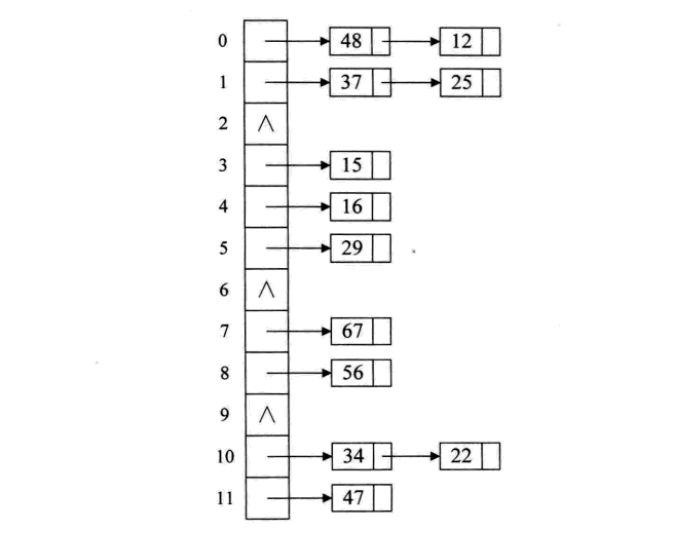
这样的好处是，不怕冲突多；缺点是降低了散列结构的随机存储性能。本质是用单链表结构辅助散列结构的不足。

4、公共溢出区法

其实就是为所有的冲突，额外开辟一块存储空间。如果相对基本表而言，冲突的数据很少的时候，使用这种方法比较合适。

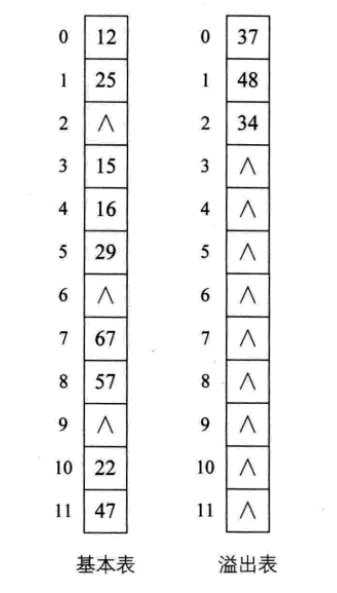
8.3 散列表查找实现

下面是一段简单的实现代码：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 忽略了对数据类型，元素溢出等问题的判断。
 
 
class HashTable:
  def __init__(self, size):
    self.elem = [None for i in range(size)] # 使用list数据结构作为哈希表元素保存方法
    self.count = size # 最大表长
 
  def hash(self, key):
    return key % self.count # 散列函数采用除留余数法
 
  def insert_hash(self, key):
    """插入关键字到哈希表内"""
    address = self.hash(key) # 求散列地址
    while self.elem[address]: # 当前位置已经有数据了，发生冲突。
      address = (address+1) % self.count # 线性探测下一地址是否可用
    self.elem[address] = key # 没有冲突则直接保存。
 
  def search_hash(self, key):
    """查找关键字，返回布尔值"""
    star = address = self.hash(key)
    while self.elem[address] != key:
      address = (address + 1) % self.count
      if not self.elem[address] or address == star: # 说明没找到或者循环到了开始的位置
        return False
    return True
 
 
if __name__ == '__main__':
  list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34]
  hash_table = HashTable(12)
  for i in list_a:
    hash_table.insert_hash(i)
 
  for i in hash_table.elem:
    if i:
      print((i, hash_table.elem.index(i)), end=" ")
  print("\n")
 
  print(hash_table.search_hash(15))
  print(hash_table.search_hash(33))

   

8.4 散列表查找性能分析

如果没发生冲突，则其查找时间复杂度为O(1)，属于最极端的好了。

但是，现实中冲突可不可避免的，下面三个方面对查找性能影响较大：

散列函数是否均匀

处理冲突的办法

散列表的装填因子（表内数据装满的程度）

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持PHP中文网。

更多一般的に使用される検索データ構造とアルゴリズムの詳細な説明 (Python 実装)相关文章请关注PHP中文网！