ホームページ >バックエンド開発 >PHPチュートリアル >フィボナッチ数列の一般用語を実現する 7 つの方法
フィボナッチ数列の一般用語を実現する 7 つの方法
- 高洛峰オリジナル
- 2017-01-14 16:41:341775ブラウズ
1: 再帰的実装
式 f[n]=f[n-1]+f[n-2] を使用し、順番に再帰的に計算します。再帰終了条件は f[1]=1, f[2] です。 =1。
2: 配列の実装
空間計算量と時間計算量は両方とも 0(n) で、効率は平均的で、再帰よりも高速です。
3: Vector
時間計算量は 0(n) ですが、ベクトルが効率的かどうかはわかりません。リソースを占有します。
4: Queue
もちろん、時間計算量と空間計算量は配列よりも Queue の方が適していますが、これには queue が最適です
f(n) =f (n-1)+f(n-2)、f(n) がキューに追加された後、f(n) は f(n-1) と f(n-2) にのみ関連します。 n-2) デキューできます。
5: 反復実装
反復実装は、時間計算量が 0(n)、空間計算量が 0(1) で最も効率的です。
六:数式の実装
Baiduを検索していたら、フィボナッチ数列には数式があり、その数式を使用して計算できることを発見しました。
double型の精度が十分ではないため、プログラムで計算した結果には誤差が生じますが、式を展開して計算すると正しい結果になります。
完全な実装コードは次のとおりです:
#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index) //递归实现
{
if(index<1)
{
return -1;
}
if(index==1 || index==2)
return 1;
return fib1(index-1)+fib1(index-2);
}
int fib2(int index) //数组实现
{
if(index<1)
{
return -1;
}
if(index<3)
{
return 1;
}
int *a=new int[index];
a[0]=a[1]=1;
for(int i=2;i<index;i++)
a[i]=a[i-1]+a[i-2];
int m=a[index-1];
delete a; //释放内存空间
return m;
}
int fib3(int index) //借用vector<int>实现
{
if(index<1)
{
return -1;
}
vector<int> a(2,1); //创建一个含有2个元素都为1的向量
a.reserve(3);
for(int i=2;i<index;i++)
{
a.insert(a.begin(),a.at(0)+a.at(1));
a.pop_back();
}
return a.at(0);
}
int fib4(int index) //队列实现
{
if(index<1)
{
return -1;
}
queue<int>q;
q.push(1);
q.push(1);
for(int i=2;i<index;i++)
{
q.push(q.front()+q.back());
q.pop();
}
return q.back();
}
int fib5(int n) //迭代实现
{
int i,a=1,b=1,c=1;
if(n<1)
{
return -1;
}
for(i=2;i<n;i++)
{
c=a+b; //辗转相加法(类似于求最大公约数的辗转相除法)
a=b;
b=c;
}
return c;
}
int fib6(int n)
{
double gh5=sqrt((double)5);
return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}
int main(void)
{
printf("%d\n",fib3(6));
system("pause");
return 0;
}7: 二部行列法
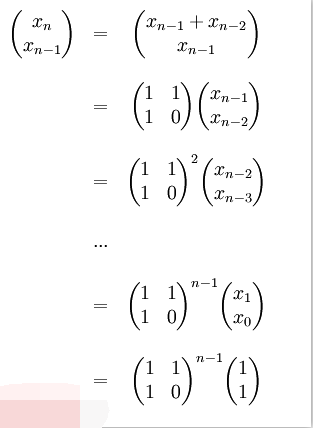
上記のように、フィボナッチ数列の任意の項目は行列累乗を使用して計算でき、n 乗はログ時間で計算できます。
コードは以下に掲載されています:
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
int tmp[4];
tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
c[0][0]=tmp[0]%mod;
c[0][1]=tmp[1]%mod;
c[1][0]=tmp[2]%mod;
c[1][1]=tmp[3]%mod;
}//计算矩阵乘法,c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
if(n==0)return 0;
else if(n<=2)return 1;//这里表示第0项为0,第1,2项为1
int a[2][2]={{1,1},{1,0}};
int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
int s;
n-=2;
while(n>0)
{
if(n%2 == 1)
multiply(result,result,a,mod);
multiply(a,a,a,mod);
n /= 2;
}//二分法求矩阵幂
s=(result[0][0]+result[0][1])%mod;//结果
return s;
}aのn乗関数を計算するための二分法を添付します。
int pow(int a,int n)
{
int ans=1;
while(n)
{
if(n&1)
ans*=a;
a*=a;
n>>=1;
}
return ans;
}フィボナッチ数列の一般項を求める 7 つの実装方法に関するその他の関連記事については、PHP 中国語 Web サイトに注目してください。

