Pythonのテキスト類似度計算における編集距離の詳細説明

編集距離

編集距離は、レーベンシュタイン距離とも呼ばれ、2 つの文字列を一方の文字列からもう一方の文字列に変換するために必要な編集操作の最小数を指します。編集操作には、ある文字を別の文字に置き換えたり、文字を挿入したり、文字を削除したりすることが含まれます。一般に、編集距離が小さいほど、2 つの文字列間の類似性は高くなります。

たとえば、単語 kitten を sittin に変換します: (「kitten」と「sitting」の間の編集距離は 3 です)

sitten (k→s)

sittin (e→i)

座っている(→g)

PythonのLevenshteinパッケージは編集距離を簡単に計算できます

パッケージのインストール: pip install python-Levenshtein<code>pip install python-Levenshtein<br>

我们来使用下：

# -*- coding:utf-8 -*-
import Levenshtein
texta = '艾伦 图灵传'
textb = '艾伦•图灵传'
print Levenshtein.distance(texta,textb)

上面的程序执行结果为3，但是只改了一个字符，为什么会发生这样的情况？

原因是Python将这两个字符串看成string类型，而在 string 类型中，默认的 utf-8 编码下，一个中文字符是用三个字节来表示的。

解决办法是将字符串转换成unicode格式，即可返回正确的结果1。

# -*- coding:utf-8 -*-
import Levenshtein
texta = u'艾伦 图灵传'
textb = u'艾伦•图灵传'
print Levenshtein.distance(texta,textb)

接下来重点介绍下保重几个方法的作用：

Levenshtein.distance(str1, str2)

计算编辑距离（也称Levenshtein距离）。是描述由一个字串转化成另一个字串最少的操作次数，在其中的操作包括插入、删除、替换。算法实现：动态规划。

Levenshtein.hamming(str1, str2)

计算汉明距离。要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。

Levenshtein.ratio(str1, str2)

计算莱文斯坦比。计算公式  r = (sum – ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和，ldist是类编辑距离。注意这里是类编辑距离，在类编辑距离中删除、插入依然+1，但是替换+2。

Levenshtein.jaro(s1, s2)

计算jaro距离，Jaro Distance据说是用来判定健康记录上两个名字是否相同，也有说是是用于人口普查，我们先来看一下Jaro Distance的定义。

两个给定字符串S1和S2的Jaro Distance为：

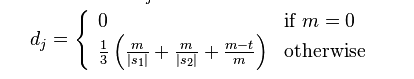
其中的m为s1, s2匹配的字符数，t是换位的数目。

两个分别来自S1和S2的字符如果相距不超过

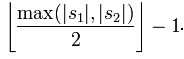
时，我们就认为这两个字符串是匹配的；而这些相互匹配的字符则决定了换位的数目t，简单来说就是不同顺序的匹配字符的数目的一半即为换位的数目t。举例来说，MARTHA与MARHTA的字符都是匹配的，但是这些匹配的字符中，T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符，t=2/2=1

それを使ってみましょう:

Levenshtein.jaro_winkler(s1, s2)

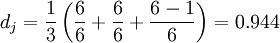
上記プログラムの実行結果は 3 文字ですが、1 文字しか変更されていません。なぜこのようなことが起こるのでしょうか。

その理由は、Python はこれら 2 つの文字列を文字列型として扱い、文字列型ではデフォルトの utf-8 エンコーディングでは中国語の文字が 3 バイトで表現されるためです。

解決策は、文字列を Unicode 形式に変換することです。これにより、正しい結果 1 が返されます。

dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961

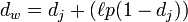
次に、いくつかのケア方法の機能に焦点を当てます:

rrreee

編集距離 (レーベンシュタイン距離とも呼ばれます) を計算します。ある文字列を別の文字列に変換するための操作の最小数について説明します。操作には、挿入、削除、置換が含まれます。アルゴリズムの実装: 動的プログラミング。

rrreee

ハミング距離を計算します。 str1 と str2 は同じ長さである必要があります。これは、2 つの等しい長さの文字列間の対応する位置にある異なる文字の数を表します。

rrreee

レーベンシュタイン比を計算します。計算式 r = (sum – ldist) / sum。ここで、sum は str1 文字列と str2 文字列の長さの合計を指し、ldist はクラス編集距離です。これはクラス編集距離であることに注意してください。クラス編集距離では、削除と挿入は +1 ですが、置換は +2 になります。

rrreee Jaro Distance は、健康記録上の 2 つの名前が同じかどうかを判断するために使用されると言われています。 まず、 の定義を見てみましょう。ジャロディスタンス。

指定された 2 つの文字列 S1 と S2 の Jaro 距離は次のとおりです: 🎜🎜🎜🎜🎜🎜 ここで、m は s1 と s2 によって一致する文字の数、t は転置の数です。 🎜🎜🎜S1 と S2 の 2 つの文字間の距離が 🎜🎜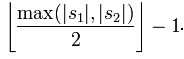🎜🎜 では、2 つの文字列が一致すると考えられ、これらの一致する文字によって転置数 t が決まります。簡単に言えば、異なる順序で一致する文字数の半分が転置されます。たとえば、MARTHA と MARHTA の文字は一致しますが、これらの一致する文字のうち、MARTHA を MARHTA に変更するには T と H を転置する必要があります。その場合、T と H は異なる順序で一致します (t =2/2)。 =1コード>。 🎜🎜🎜 2 つの文字列の Jaro 距離は次のとおりです: 🎜🎜🎜🎜🎜🎜🎜🎜rrreee🎜🎜🎜 Jaro-Winkler 距離を計算すると、Jaro-Winkler は同じ開始部分を持つ文字列に高いスコアを与えます。接頭辞 p を定義しました。 、 2 つの文字列が与えられ、プレフィックス部分の長さが ι の同じ部分がある場合、Jaro-Winkler 距離は次のようになります: 🎜🎜🎜🎜🎜🎜🎜 dj は 2 つの文字列の Jaro 距離です🎜🎜 🎜 ith は同じ長さですプレフィックスが付いていますが、最大制限は 4 です🎜🎜🎜 p は分数を調整するための定数であり、25 を超えることはできません。それ以外の場合、dw は 1 より大きくなる可能性があります。ウィンクラーは、この定数を 0.1🎜🎜🎜 として定義します。このように、Jaro-Winkler 距離上記の MARTHA と MARHTA のアルゴリズムは、 🎜🎜🎜rrreee🎜🎜🎜🎜 個人的にアルゴリズムを改善できると思います: 🎜🎜🎜🎜 ストップワードを削除する (主に句読点の影響) 🎜🎜🎜 中国語を分析する場合、より良いですか?文字ではなく単語で比較するには？ 🎜🎜🎜🎜概要🎜🎜🎜🎜上記がこの記事の全内容です。この記事の内容が Python の学習または使用に役立つことを願っています。ご質問がある場合は、メッセージを残して連絡してください。 。 🎜