Java プログラミングのインタビューで一般的に使用される上位 10 のアルゴリズム概念の要約

以下は、プログラミング面接におけるアルゴリズム関連の概念トップ 10 です。いくつかの簡単な例を通してこれらの概念を説明します。これらの概念を完全に習得するにはさらに多くの努力が必要となるため、このリストは入門のみを目的としています。この記事では、次の概念を含めて、Java の観点から問題を検討します:

1. String

IDE にコードの自動補完機能がない場合は、次のメソッドを覚えておく必要があります。

toCharArray() // 获得字符串对应的char数组
Arrays.sort()  // 数组排序Arrays.toString(char[] a) // 数组转成字符串
charAt(int x) // 获得某个索引处的字符
length() // 字符串长度
length // 数组大小

2. リンク リスト

Java では、リンク リストの実装は非常に簡単です。各ノード Node には値 val と、次のノードを指すリンク next があります。

class Node {
    int val;
    Node next;
    Node(int x) {
        val = x;
        next = null;
    }
}

リンク リストの 2 つの有名なアプリケーションは、Stack と Queue です。

スタック:

class Stack{
    Node top; 
    public Node peek(){
        if(top != null){
            return top;
        }
        return null;
    }
    public Node pop(){
        if(top == null){
            return null;
        }else{
            Node temp = new Node(top.val);
            top = top.next;
            return temp;
        }
    }
    public void push(Node n){
        if(n != null){
            n.next = top;
            top = n;
        }
    }
}

キュー:

class Queue{
    Node first, last;
    public void enqueue(Node n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public Node dequeue(){
        if(first == null){
            return null;
        }else{
            Node temp = new Node(first.val);
            first = first.next;
            return temp;
        }
    }
}

3. ツリー

ここでのツリーは通常、次のような左の子ノードと右の子ノードを指します。いくつかの関連概念を持つツリー:

バランス型 vs. アンバランス型: バランス型バイナリ ツリーでは、各ノードの左右のサブツリー間の深さの差は最大 1 (1 または 0) です。

完全なバイナリ ツリー: リーフ ノードを除くすべてのノードには 2 つの子があります。

完璧なバイナリ ツリー: これは次の特性を持つ完全なバイナリ ツリーです: すべてのリーフ ノードは同じ深さまたは同じレベルにあり、各親ノードには 2 つの子が必要です。

完全なバイナリ ツリー: バイナリ ツリーでは、おそらく最後のレベルを除くすべてのレベルが完全に埋められており、すべてのノードが可能な限り左に近くなければなりません。

訳者注: 完全な二分木は、漠然と完全二分木とも呼ばれます。すべての人には 2 人の生物学的な親が必要であるため、完全な二分木の例としては、特定の深さにおける人の祖先グラフが挙げられます。完全な二分木は、左に傾いた多数の追加の葉ノードを持つことができる完全な二分木と考えることができます。質問: 完全なバイナリ ツリーと完全なバイナリ ツリーの違いは何ですか? (参考: http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html)

4. グラフ

グラフ関連の問題は主に深さ優先探索 (深さ優先探索) と幅優先探索 (ブレス) に焦点を当てています。まず) 検索)。

以下は、グラフ幅優先検索の簡単な実装です。

1) GraphNode を定義します

class TreeNode{
    int value;
    TreeNode left;
    TreeNode right;
}

2) キュー Queue を定義します

class GraphNode{ 
    int val;
    GraphNode next;
    GraphNode[] neighbors;
    boolean visited;
    GraphNode(int x) {
        val = x;
    }
    GraphNode(int x, GraphNode[] n){
        val = x;
        neighbors = n;
    }
    public String toString(){
        return "value: "+ this.val; 
    }
}

3) キュー Queue を使用して幅優先検索を実装します

class Queue{
    GraphNode first, last;
    public void enqueue(GraphNode n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public GraphNode dequeue(){
        if(first == null){
            return null;
        }else{
            GraphNode temp = new GraphNode(first.val, first.neighbors);
            first = first.next;
            return temp;
        }
    }
}

出力:

1 値: 2 値: 3 値: 5 検索値: 5

2 値: 4

5. 並べ替え

以下は、さまざまな並べ替えアルゴリズムの時間計算量です。これらのアルゴリズムの基本的な考え方を確認するには、Wiki を参照してください。

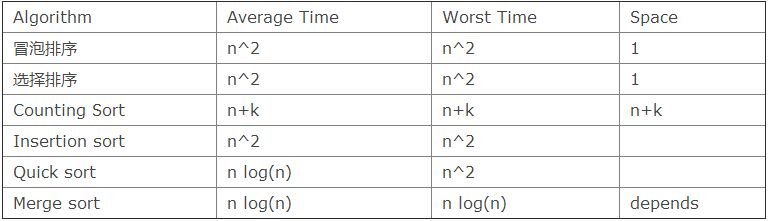また、ここにいくつかの実装/デモがあります: カウンティングソート、マージソート、クイックソート、挿入ソート。

「一般的に使用される 7 つの並べ替えアルゴリズムを視覚的に直感的に体験」

「ビデオ: 15 の並べ替えアルゴリズムの 6 分間のデモンストレーション」

6. 再帰と反復

プログラマーにとって、再帰は生来の組み込み思考である必要があります。簡単な例で説明できます。

質問: n 段ありますが、一度に 1 段か 2 段しか上がれません。方法は何通りありますか?

ステップ 1: 最初の n ステップと最初の n-1 ステップの間の関係を見つけます。

n 段を歩くには 2 つの方法しかありません: n-1 段から 1 段登ってそこに着くか、n-2 段から 2 段登ってそこに着くかです。 f(n) が n 番目のステップに登る方法の数である場合、f(n) = f(n-1) + f(n-2) となります。

ステップ 2: 開始条件が正しいことを確認します。

f(0) = 0;

f(1) = 1;

public class GraphTest {
    public static void main(String[] args) {
        GraphNode n1 = new GraphNode(1); 
        GraphNode n2 = new GraphNode(2); 
        GraphNode n3 = new GraphNode(3); 
        GraphNode n4 = new GraphNode(4); 
        GraphNode n5 = new GraphNode(5); 
        n1.neighbors = new GraphNode[]{n2,n3,n5};
        n2.neighbors = new GraphNode[]{n1,n4};
        n3.neighbors = new GraphNode[]{n1,n4,n5};
        n4.neighbors = new GraphNode[]{n2,n3,n5};
        n5.neighbors = new GraphNode[]{n1,n3,n4};
        breathFirstSearch(n1, 5);
    }
    public static void breathFirstSearch(GraphNode root, int x){
        if(root.val == x)
            System.out.println("find in root");
        Queue queue = new Queue();
        root.visited = true;
        queue.enqueue(root);
        while(queue.first != null){
            GraphNode c = (GraphNode) queue.dequeue();
            for(GraphNode n: c.neighbors){
                if(!n.visited){
                    System.out.print(n + " ");
                    n.visited = true;
                    if(n.val == x)
                        System.out.println("Find "+n);
                    queue.enqueue(n);
                }
            }
        }
    }
}

次のように、多くの冗長な計算があるため、再帰的メソッドの時間計算量は n で指数関数的になります:

public static int f(int n){
    if(n <= 2) return n;
    int x = f(n-1) + f(n-2);
    return x;
}

直接的なアイデアは、次のように変換することです。再帰から反復へ:

f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)

この例では、反復にかかる時間は短くなります。再帰と反復を参照することもできます。

7. 動的プログラミング

動的プログラミングは、次のような性質の問題を解決するための手法です:

問題は、より小さな部分問題を解決することで解決できます (翻訳者注: 問題に対する最適な解決策には、その部分問題が含まれます)最適解、つまり最適な基礎構造特性）。

一部の部分問題の解は複数回計算する必要がある場合があります (翻訳者注: これは部分問題の重複する性質です)。

部分問題の解はテーブルに保存されるため、各部分問題の計算は 1 回だけで済みます。

時間を節約するには追加のスペースが必要です。

段差昇降問題は上記の4つの性質に完全に適合するため、動的計画法で解くことができます。

public static int f(int n) {
    if (n <= 2){
        return n;
    }
    int first = 1, second = 2;
    int third = 0;
    for (int i = 3; i <= n; i++) {
        third = first + second;
        first = second;
        second = third;
    }
    return third;
}

8. ビット演算

ビット演算子:

获得给定数字n的第i位：(i从0计数并从右边开始)

public static boolean getBit(int num, int i){
    int result = num & (1<<i);
    if(result == 0){
        return false;
    }else{
        return true;
    }

例如，获得数字10的第2位：

i=1, n=10
11010&10=10
10 is not 0, so return true;

9. 概率问题

解决概率相关的问题通常需要很好的规划了解问题（formatting the problem），这里刚好有一个这类问题的简单例子：

一个房间里有50个人，那么至少有两个人生日相同的概率是多少？（忽略闰年的事实，也就是一年365天）

计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里，我们可以计算所有人生日都互不相同的概率，也就是：365/365 * 364/365 * 363/365 * … * (365-49)/365，这样至少两个人生日相同的概率就是1 – 这个值。

public static double caculateProbability(int n){
    double x = 1; 
    for(int i=0; i<n; i++){
        x *=  (365.0-i)/365.0;
    }
    double pro = Math.round((1-x) * 100);
    return pro/100;

calculateProbability(50) = 0.97

10. 排列组合

组合和排列的区别在于次序是否关键。

如果你有任何问题请在下面评论。

参考/推荐资料：
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell