クイックソート (QuickSort) - Java 実装

背景

クイックソートは、1960年代にアメリカのトニー・ホールによって提案された並べ替え方法です。このソート方法は、当時すでに非常に高速なソート方法でした。したがって、ネーミング的には「クイックソート」と呼ばれます。このアルゴリズムは 20 世紀の 7 つの主要なアルゴリズムの 1 つであり、平均時間計算量は Ο(nlogn) であり、実際の演算速度は同じ時間計算量の他のソート方法よりも高速です。 。

トニー ホールとクイック ソートの背景に興味のある学生は、この概要を確認してください: http://www.nowwamagic.net/librarys/veda/detail/2391

思考の並べ替え

クイック のアイデアソートは考えるのが難しいですが、理解するのは非常に簡単です。彼のアイデアは次のとおりです。

1. まず、キュー内の特定の要素をベース値として選択します (通常は先頭要素または末尾要素を選択します)。

2. 基本値を順番にすべての要素と比較します。要素は比較結果に応じて 2 つのキュー A と B に分割されます。 1 つはすべての要素が基本値より大きいもの、もう 1 つはすべての要素が基本値より小さいものです。

3. A を新しいキューとして使用し、ベースを再度選択し、それを 2 つの小さなキューに分割します。

4. このようにして、それぞれの小さなキューを 2 つの小さなキューに無限に分割し続けます。

5. キューが解凍できない部分（つまり 1 つの要素）に分割されるまで

6. キュー間の順序が固定されているため。これらのキューを一度に結合すると、全体のソートが完了します。

(盗難防止関連: この記事は http://www.cnblogs.com/jilodream/ から最初に公開されました)

ここには 2 つの主要な手順があることに注意してください。それは

1 値要素を選択して除算します。キュー全体を 2 つのサブキュー

2 に分割します。 次に、そのサブキューを全体のサイズが現在のキューよりも小さい新しいキューとして再利用し、計算が非常に簡単になるまで計算を実行します。

これら 2 つの主要な手順により、クイック ソート固有の利点が生まれます:

1. サブキューに分割された要素のサイズを比較することにより、今後の比較プロセスでは、この要素の比較範囲は常にこのサブキュー内に留まります。より冗長な比較。これにより、初期の比較がその後の比較に依然として強い影響を与えることができます。バブルソート法と同様に、初期段階で多くの比較を行っても、後の段階ではほとんど影響しません。これは kmp アルゴリズムに非常に似ています。初期の比較では最大限に活用してください。

2. 元のスケール キューをいくつかの小さなサブキューに分割します。これらのサブキューは、(盗難防止接続: この記事は http://www.cnblogs.com/jilodream から最初に公開されました) と同じ問題を解決する必要があります。 /) 元のキューは同じですが、サイズが小さくなります。このような絶え間ない分裂は、分割統治の精神を生み出します。この考え方はバックパックのアルゴリズムとも一致します。

テキストを理解するのが難しい生徒のために、非常に鮮やかな以下の古典的なオンラインの動的な画像を見てください:

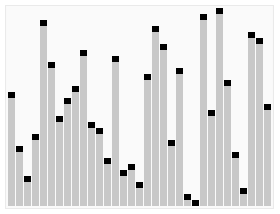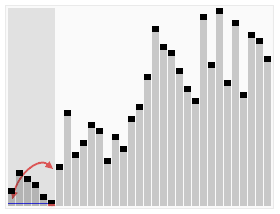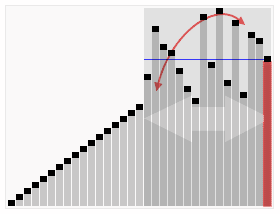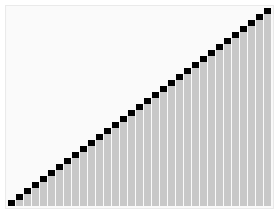以下は java

import java.util.Arrays;

public class QuickSort
{
    public static void main(String args[])
    {
        QuickSort quicksort = new QuickSort();
        int[] arrays = new int[]
        { 1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19 };
        quicksort.quickSort(arrays);
        System.out.println(Arrays.toString(arrays));
    }
    
    private void quickSort(int[] arrays)
    {
        subQuickSort(arrays, 0, arrays.length - 1);
    }
    
    private void subQuickSort(int[] arrays, int start, int end)
    {
        if (start >= end)
        {
            return;
        }
        int middleIndex = subQuickSortCore(arrays, start, end);
        subQuickSort(arrays, start, middleIndex - 1);
        subQuickSort(arrays, middleIndex + 1, end);
    }
    
    private int subQuickSortCore(int[] arrays, int start, int end)
    {
        int middleValue = arrays[start];
        while (start < end)
        {
            while (arrays[end] >= middleValue && start < end)
            {
                end--;
            }
            arrays[start] = arrays[end];
            while (arrays[start] <= middleValue && start < end)
            {
                start++;
            }
            arrays[end] = arrays[start];
        }
        arrays[start] = middleValue;
        return start;
    }
}

で実装されたコードです。