JavaScript を使ってゲーム物理を遊ぶ (1) 運動学シミュレーションとパーティクル システム_JavaScript スキル

シリーズ紹介
おそらく、300 年前のアイザック ニュートン卿 (1643-1727) は、今日の多くのゲームやアニメーションで物理学が広く使用されているとは想像していなかったでしょう。なぜこれらのアプリケーションで物理学を使用するのでしょうか?著者は、私たちは生まれたときから物理世界の法則を感じ、この世界で物体がどのように「正常に動くか」を認識していると考えています。たとえば、ボールを撃つとき、ボールは放物線になります（回転するボールは回転する可能性があります）。曲がったボール）、紐の端に結ばれた石は一定の周波数で振動します、など。ゲームやアニメーション内のオブジェクトがリアルに感じられるためには、私たちが期待する「通常の動き」と一致する方法でオブジェクトが動く必要があります。
今日のゲームアニメーションには、運動学シミュレーション、剛体ダイナミクスシミュレーション、ストリング/クロスシミュレーション、ソフトボディダイナミクスシミュレーション(ソフトボディダイナミクスシミュレーション)、流体ダイナミクスシミュレーション(流体力学シミュレーション)など、さまざまな物理シミュレーション技術が適用されています。 、など。さらに、多くのシミュレーション システムでは衝突検出が必要です。
このシリーズでは、この分野の最も基本的な知識をいくつか紹介し、引き続き JavaScript を例として使用し、リアルタイムのインタラクティブな方法で体験していきたいと考えています。
この記事の紹介
シリーズの最初の記事として、この記事では、非常に単純な数式が 2 つだけある、最も単純な運動学シミュレーションを紹介します。キネマティック シミュレーションは、さまざまなオブジェクト (マリオのジャンプ、砲弾など) の動きをシミュレートするために使用できます。この記事では、パーティクル システムを使用して視覚的な特殊効果を作成します (パーティクル システムは実際にゲームをプレイするために使用できます)。視覚的な特殊効果だけではありません)。
運動学シミュレーション
運動学では物体の動きを研究します。力学との違いは、運動学では物体の質量や慣性モーメントが考慮されないことと、物体に加えられる力やトルクが考慮されないことです。
まずニュートンの運動の第一法則を思い出してみましょう:
物体に外力が作用していないとき、または正味の力がゼロのとき、もともと静止していたものは常に静止し、元は静止していました。運動中は常に一定の速度で直線に沿って移動します。この法則は「慣性の法則」とも呼ばれます。この法則は、すべてのオブジェクトはその位置に加えて、線速度状態も持つことを示しています。ただし、力の影響を受けないオブジェクトだけをシミュレートするのは面白くありません。力の概念を脇に置いて、線形加速度を使用して物体の動きに影響を与えることができます。たとえば、任意の時刻 t における自由落下物体の y 軸座標を計算するには、次の解析ソリューションを使用できます。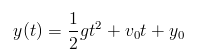

ここで、 と はそれぞれ t における y 軸座標です。 =0 の初期座標と速度、g は重力加速度です。
この解析ソリューションは単純ですが、いくつかの欠点があります。たとえば、g は定数であり、シミュレーション プロセス中に変更することはできません。また、オブジェクトが障害物に遭遇して衝突した場合、この式を適用することは困難です。この不連続性（不連続性）を処理します。
コンピューター シミュレーションでは、連続的なオブジェクトの状態を計算する必要があることがよくあります。ゲーム用語では、最初のフレームの状態、2 番目のフレームの状態などを計算することを意味します。任意の時刻 t におけるオブジェクトの状態を仮定します。位置ベクトルは 、速度ベクトルは 、加速度ベクトルは です。ある時点の状態から次のシミュレーション時点の状態を計算したいとします。最も簡単な方法は、数値積分にオイラー法を使用することです。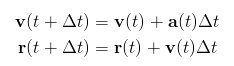

オイラー法は非常に単純ですが、精度と安定性の問題がありますが、この記事では無視します。この記事の例では 2 次元空間を使用します。まず、JavaScript の 2 次元ベクトル クラスを実装します。

コードをコピーします。コードは次のとおりです。

// Vector2.js
Vector2 = function(x, y) { this.x = x; this.y = y }; >Vector2.prototype = {
copy : function() { return new Vector2(this.x, this.y) },
length : function() { return Math.sqrt(this.x * this. x this.y * this.y ); },
sqrLength : function() { return this.x * this.x this.y * this.y },
normalize : function() { var inv = 1/this.length() ; return new Vector2(this.x * inv, this.y * inv); },
negate : function() { return new Vector2(-this.x, -this.y) ); },
add : function(v) { return new Vector2(this.x v.x, this.y v.y); },
subtract : function(v) { return new Vector2(this.x - v.x) , this.y - v.y); },
multiply : function(f) { return new Vector2(this.x * f, this.y * f) },
divide : function(f) { var invf = 1/f; return new Vector2(this.x * invf, this.y * invf); },
dot : function(v) { return this.x * v.x this.y * v.y; >};

Vector2.zero = new Vector2(0, 0);


次に、HTML5 Canvas を使用してシミュレーション プロセスを表現できます。 🎜>

コードをコピーします

コードは次のとおりです:

var 位置 = 新しい Vector2(10, 200);
var 速度 = 新しい Vector2(50, -50);
var 加速 = new Vector2(0, 10);
var dt = 0.1;
function step() {
position = Position.add(velocity.multiply(dt));
速度 = Velocity.add(acceleration.multiply(dt));
ctx.ストロークスタイル = "#000000";
ctx.fillStyle = "#FFFFFF";
ctx.beginPath();
ctx.arc(position.x,position.y, 5, 0, Math.PI*2, true);
ctx.closePath();
ctx.fill();
ctx.ストローク();
}
start("kinematicsCancas", step);

実行
<ボタン onclick="stop();" type="button">停止
<ボタン onclick="clearCanvas();" type="button">クリア

修正代网试试看 開始位置を変更 開始速度を変更(方向を含む) 加速度を変更

このプログラムの中核は step() 関数の 2 つの実行コードです。パーティクル システムは、アニメーションやアニメーションで、雨点、火花、火花、爆発などのさまざまな効果をもたらすためによく使用されます。関連する機能は、たとえば、人が殴られた後にいくつかの光を発し、メインコーナーがそれらを吸収することができます。特性:

粒子は独立、粒子間相互不影響响(不碰撞、不徹底)

粒子有生命期間、生命结束後消滅

粒子は空間の 1 つの点として理解できますが、場合によっては、球体と環境の影響として半径を設定することもできます。

粒子帯には動作状態があり、その他の外部表示状態 (例:色、影など)もあります

粒子は回転運動を考慮せずに線性運動のみを行うことができます(例外もあります)

以下は本文例子里实现的粒子类:




复制代码

代码如下:// Particle.js Particle = function(位置、速度、寿命、色、サイズ) { this.position = 位置;

this.velocity = 速度;

this.acceleration = Vector2.zero;
this.age = 0;
this.life = 人生;
this.color = カラー;
this.size = サイズ;
};


游戏循環环
粒子系统は通常 3 つの周期に分けることができます:
送信粒子

模拟粒子(粒子老化、碰撞、运運動学模拟等等)
渲染パーティクル
は、ゲーム ループ内で各パーティクル システムに対して上記の 3 つのステップを実行する必要があります。パーティクルを生成します。パーティクルは、数値グループの末端に追加されるだけです。 🎜>//ParticleSystem.js
function ParticleSystem() {
// プライベート フィールド
var that = this;
var 粒子 = new Array();
// パブリックフィールド
this.gravity = new Vector2(0, 100);
this.Effects = new Array();

// パブリック メソッド this.emit = function(particle) { particles.push(particle); }; // ... }

粒子は初期化時に、年 (年齢) はゼロに設定され、生命 (寿命) は固定されています。各シミュレーションが行われるたびに、都市は粒子を老化させます。つまり、年月が増加すると、年月が生命を超えて死に至ります。 🎜>


复制代码


代码如下:

function ParticleSystem() {
// ...
this.simulate = function(dt) {
aging(dt);
applyGravity();
applyEffectors();
kinematics(dt);
};
// ...
// プライベート メソッド
function age(dt) {
for (var i = 0; i <粒子.長さ; ) {
var p = 粒子[i];
if (p.age >= p.life)
kill(i); 🎜>else
i ;
}
}
function kill(index) {
if (particles.length > 1)
particles[index] =articles[particles.length - 1];
particles.pop();
}
// ...
}


関数 kill() でトリックが使用されます。配列内のパーティクルの順序は重要ではないため、中央のパーティクルを削除するには、最後のパーティクルをその要素にコピーし、pop() を使用して最後のパーティクルを削除します。これは通常、配列の途中から要素を直接削除するよりも高速です (C の配列または std::vector にも同じことが当てはまります)。

運動学シミュレーション
この記事の運動学シミュレーション コードの最も重要な 2 つの文をすべてのパーティクルに適用するだけです。さらに、各シミュレーションでは、まず重力加速度が粒子の加速度に書き込まれます。これは、将来的に毎回加速度を変更できるようにするために行われます (これについては、続編で説明します)。

コードをコピー コードは次のとおりです。function ParticleSystem() {

// .. .

function applyGravity() {
for (粒子内の変数 i)
particles[i].acceleration = that.gravity;
function kinematics(dt) {
for (パーティクル内の var i) {
var p = パーティクル[i]
p.position = p.position.add(p.velocity.multiply(dt));
p.velocity = p.パーティクルのレンダリング
}円、線分 (現在位置と前の位置)、画像、スプライトなどを使用するなど、さまざまな方法でレンダリングが行われます。この記事では円を使用し、寿命と年齢の比率に応じて円の透明度を制御します。コード スニペットは次のとおりです。




コードをコピーします
。

コードは次のとおりです。

function ParticleSystem() {
// ...

this.render = function(ctx) { for (var i粒子内) { var p = 粒子[ i]; var alpha = 1 - p.age / p.life; ctx.fillStyle = "rgba(" Math.floor(p) .color.r * 255) "," Math.floor(p.color.g * 255) ","

Math.floor(p.color.b * 255) ","

アルファ.toFixed(2) ")";
ctx.beginPath();
ctx.arc(p.position.x, p.position.y, p.size, 0, Math.PI * 2, true );
ctx.closePath();
ctx.fill();
// ...
}


基本的なパーティクル システムが完成しました
以下の例では、各フレームがパーティクルを放出します。その位置はキャンバスの中央 (200,200)、放出方向は 360 度、速度は 100、ライフは 1 です。 2 番目の色は赤、半径は 5 ピクセルです。




コードをコピーします


コードは次のとおりです。

var ps = new ParticleSystem(); 🎜>var dt = 0.01;
function sampleDirection() {
var theta = Math.random() * 2 * Math.PI;

return new Vector2(Math.cos(theta), Math.sin (θ) ); } 関数 step() { ps.emit(new Particle(new Vector2(200, 200), SampleDirection().multiply(100), 1, Color.red, 5)); ps.simulate(dt); ps.render(ctx); start("basicParticleSystemCanvas", ステップ);

実行

停止



;


単純衝突
解析ソリューションよりも数値積分を使用する利点を説明するために、この記事では粒子システムに単純衝突を追加します。要件を追加したいと思います。パーティクルが長方形のチャンバー (キャンバス全体のサイズに設定可能) の内壁に衝突すると、衝突して反発します。衝突は完全に弾力的です。
プログラミングの観点からは、この関数を実行するためにコールバックを使用します。 ParticleSystem クラスにはエフェクタの配列があります。キネマティクス シミュレーションを実行する前に、各エフェクタ オブジェクトの apply() 関数が実行されます。
長方形のチャンバーは次のように実装されます。

コードをコピーします コードは次のとおりです:

// ChamberBox.js
function ChamberBox(x1, y1, x2, y2) {
this. apply = function(particle) {
if (particle.position.x -article.size x2)
particle.velocity.x = -particle.速度.x;
if (粒子.位置.y - 粒子.サイズ y2)
粒子.速度.y = -粒子.速度.y ;
};
}

これは実際には、粒子が内壁の範囲を超えたことを検出したときにその方向の速度成分を反転します。
さらに、この例のメイン ループは毎回キャンバス全体をクリアするのではなく、モーション ブラーの効果をシミュレートするためにフレームごとに半透明の黒い四角形を描画します。粒子の色も2色からランダムにサンプリングされます。

コードをコピーします コードは次のとおりです。

var ps = new ParticleSystem(); 🎜>ps .effects.push(new ChamberBox(0, 0, 400, 400)); // 最も重要なことは、このステートメントの追加です。
var dt = 0.01; function sampleDirection(angle1, angle2) ) {
var t = Math.random();
var theta = angle1 * t angle2 * (1 - t);
return new Vector2(Math.cos(theta), Math.sin(theta) ));
}
関数 sampleColor(color1, color2) {
var t = Math.random();
return color1.multiply(t).add(color2.multiply(1 - t) ));
}
関数 step() {
ps.emit(new Particle(new Vector2(200, 200)、sampleDirection(Math.PI * 1.75、Math.PI * 2).multiply( 250), 3, サンプルカラー (Color.blue, Color.purple), 5));
ctx.fillRect (0,0,canvas.width,canvas.height);
ps.render(ctx);
start("collisionChamberCanvas", step); 🎜><ボタン onclick ="eval(document.getElementById('collisionChamberCode').value)" type="button">実行
停止



インタラクティブな起動
最後に追加された例 インタラクティブ機能はマウスの位置でパーティクルを放出し、パーティクルの方向はマウスの移動速度に少しのノイズを加えたものに基づいています。粒子サイズと寿命にランダム性が追加されます。

コードをコピー


コードは次のとおりです:

var ps = new ParticleSystem();
ps.effectors.push(new ChamberBox(0, 0, 400, 400));
var dt = 0.01;
var oldMousePosition = Vector2.zero, newMousePosition = Vector2.zero;
function sampleDirection(angle1, angle2) {
var t = Math.random();
var theta = angle1 * t angle2 * (1 - t);
return new Vector2(Math.cos(theta), Math.sin(theta));
}
function sampleColor(color1, color2) {
var t = Math.random();
return color1.multiply(t).add(color2.multiply(1 - t));
}
function sampleNumber(value1, value2) {
var t = Math.random();
return value1 * t value2 * (1 - t);
}
function step() {
var velocity = newMousePosition.subtract(oldMousePosition).multiply(10);
velocity = velocity.add(sampleDirection(0, Math.PI * 2).multiply(20));
var color = sampleColor(Color.red, Color.yellow);
var life = sampleNumber(1, 2);
var size = sampleNumber(2, 4);
ps.emit(new Particle(newMousePosition, velocity, life, color, size));
oldMousePosition = newMousePosition;
ps.simulate(dt);
ctx.fillStyle="rgba(0, 0, 0, 0.1)";
ctx.fillRect(0,0,canvas.width,canvas.height);
ps.render(ctx);
}
start("interactiveEmitCanvas", step);
canvas.onmousemove = function(e) {
if (e.layerX || e.layerX == 0) { // Firefox
e.target.style.position='relative';
newMousePosition = new Vector2(e.layerX, e.layerY);
}
else
newMousePosition = new Vector2(e.offsetX, e.offsetY);
};
Run
Stop

总结
本文介绍了最简单的运动学模拟，使用欧拉方法作数值积分，并以此法去实现一个有简单碰撞的粒子系统。本文的精华其实只有两条简单公式(只有两个加数和两个乘数)，希望让读者明白，其实物理模拟可以很简单。虽然本文的例子是在二维空间，但这例子能扩展至三维空间，只须把Vector2换成Vector3。本文完整源代码可下载。
续篇会谈及在此基础上加入其他物理现象，有机会再加入其他物理模拟课题。希望各位支持，并给本人更多意见。

声明：

この記事の内容はネチズンが自主的に寄稿したものであり、著作権は原著者に帰属します。このサイトは、それに相当する法的責任を負いません。盗作または侵害の疑いのあるコンテンツを見つけた場合は、admin@php.cn までご連絡ください。

前の記事：js操作時間(年-月-日時-分-第2曜日)_javascriptスキル次の記事：js操作時間(年-月-日時-分-第2曜日)_javascriptスキル

関連記事

続きを見る

• Bootstrap リスト グループ コンポーネントの詳細な分析
• JavaScript関数のカリー化の詳細説明
• JS パスワードの生成と強度検出の完全な例 (デモ ソース コードのダウンロード付き)
• Angularjs は WeChat UI (weui) を統合します
• JavaScript を使用して繁体字中国語と簡体字中国語をすばやく切り替える方法と、簡体字中国語と繁体字中国語の切り替えをサポートする Web サイトのトリック_javascript スキル

福祉オンライン PHP トレーニング，PHP 学習者の迅速な成長を支援します！

私たちについて免責事項Sitemap

© php.cn All rights reserved

コードを変更して試してください 起動位置を変更します< /li> 上向きに発射、発射範囲は 90 度以内です ライフを変更 半径を変更 フレームごとに 5 つのパーティクルを放出します