最大部分列とアルゴリズム分析
問題の説明: n 個の整数列 {a1, a2,...,an} が与えられた場合、関数 f(i,j)=max{0,Σa k}(k: i から j まで連続して取得);
問題は、連続するサブ列の合計の最大値を見つけることです。最大値が負の数の場合は、0 を取得します。 8 つの数列 {-1,2,-3,4,-2,5,-8,3} として、Namo の最大部分列合計は 4 (-2) 5=7 です。
この問題には複雑度の異なる 4 つのアルゴリズムがあり、アルゴリズム 1 ~ 4 の時間計算量は O(n3)、O(n2)、O(nlogn) です。 、O(n);
アルゴリズム 1:
最も直接的な方法は、すべての状況をリストする網羅的な方法であり、次の式の左端 i を設定できます。 //最大のサブ列と網羅的なメソッド#include
名前空間 std を使用;
int Find_Maxsun(int*a, int n);
int main(){
int n, i;
int a[100];
cin >> n ;
cout を入力してください。 n; i )
cin >> a[i];
cout return 0;
}
Find_Maxsun(int*a , int n){
int MaxSun = 0, i, j, k;
int NowSum;
for (i = 0; i
for (k = i; k NowSum = a[k]; /* a[i] から a[j] までのシーケンス */
if (NowSum>MaxSun)
MaxSun = NowSum;
}
return MaxSun;
}
3) です。もちろん、最も愚かなアルゴリズムですが、データが非常に難しい場合、たとえそれが死ぬほど計算されたとしても、
j が追加されるたびに、for ループの 3 番目のレベルが明らかにわかります。 -列の合計を再度計算する必要があるので、j-1 の結果を使用しないのはなぜでしょうか。つまり、j-1 の結果を保存します。ステップ j の結果を計算するときは、ステップ j-1 に基づいて a[j] を加算するだけで済みます。したがって、アルゴリズム 2 が存在します。アルゴリズム 2:
#includeusing namespace std;
int Find_Maxsun2(int*a, int n);
int main(){
int n, i;
int a[100];
cin >> n;
cout for (i = 0; i
cout return 0;
}
int Find_Maxsun2(int*a, int n){
int i, j, NewSum = 0, MaxSum = 0;
for (i = 0; i
for (j = i; j NewSum = a[j] /* j-1 条件で毎回 NewSum を更新します*/
if (NewSum>MaxSum) / *MaxSum を更新* /
MaxSum = NewSum;
}
}
return MaxSum;
}
2)、これは明らかに私たちが望む複雑さではありません。
アルゴリズム 3:
アルゴリズム 3 は分割統治の考え方を使用します。基本的な考え方は自明です。最初に分割してから征服し、分解します。問題を小さな問題に分割し、合計できる小さな問題を解決するには、元のシーケンスを 2 つに分割し、最大のサブシーケンスを左側、右側、または境界を越えて配置します。 基本的な考え方は次のとおりです。 🎜>ステップ 1: 元のシーケンスを 2 つに分割し、左のシーケンスと右のシーケンスに分割します。
ステップ 2: サブシーケンス S left と S right を再帰的に見つけます。
パート 3: 中心線から両側に向かってスキャンして、中心線と S を横切る最大のサブシーケンスを見つけます。
ステップ 4: S=max{S left, S middle, S right} を見つける
コードは次のように実装されます。
#include
名前空間 std を使用;
int Find_MaxSum3(int*a,int low,int high);
int Max(int a,int b,int c);
int main(){
int n, i;
int a[100];
cin >> n;
cout for (i = 0; i
return 0;
}
int Find_MaxSum3(int*a,int low,int high) int MaxSum = 0, MidSum, LeftSum, RightSum,i;
MidSum = 0;
if (low == high){ /*再帰の終了条件*/
if (a[low] > 0)
return a[low];
else
return 0;
}
int mid = (low high) / 2 //スコアの中間点を見つける
LeftSum = Find_MaxSum3( a, low, mid); /*左のシーケンスの最大合計を再帰的に求めます*/
RightSum = Find_MaxSum3(a, mid 1, high); /*右のシーケンスの最大のサブシーケンスの合計を再帰的に求めます*/
/*そうすれば、中間の国境を越えたシーケンスの最大合計を見つけることができます */
int NewLeft = 0,Max_BorderLeft=0, NewRight = 0,Max_BorderRight=0;
for (i = Mid; i >= low; i--) { /*左をスキャンして最大合計を見つけます*/
NewLeft = a[i];
if (NewLeft > Max_BorderLeft)
Max_BorderLeft = NewLeft ;
}
for (i = mid 1; i NewRight =a[i];
if (NewRight >= Max_BorderRight)
Max_BorderRight = NewRight ;
}
MidSum = Max_BorderRight Max_BorderLeft;
return Max(LeftSum, MidSum, RightSum) /*処理の結果を返します*/
}
int Max(int a, int b, int c){ /*3 つの中で最大の数値を見つける*/
if ( a>= b&&a >= c)
return a ;
if (b >= a&&b >= c )
return b;
if (c >= b&&c>=a)
return c;
}
kT( n/2k) kO(n)=2kT(1) kO(n) (n=2 の場合) k)=n nlogn=O (nlogn);
このアルゴリズムは非常に優れていますが、最速のアルゴリズムではありません。アルゴリズム 4:
アルゴリズム 4 はオンライン処理と呼ばれます。これは、データが読み込まれるたびに、時間内に処理され、得られた結果が現在読み込まれているデータに当てはまります。つまり、アルゴリズムはどの位置でも正しい解を与えることができ、アルゴリズムは次のことを行うことができます。読みながら正しい解決策を見つけてください。 #include名前空間 std を使用;
int Find_MaxSum4(int*a, int n);
int main(){
int n, i;
int a[100];
cin >>
cout for (i = 0; i
cout return 0;
}
int Find_MaxSum4(int*a, int n){
int i, NewSum = 0, MaxSum = 0;
for (i = 0; i NewSum = a[i]; /*現在のサブシーケンス合計*/
if (MaxSum
if ( NewSum NewSum = 0;
}
return MaxSum;
}
 华为GT3 Pro和GT4的差异是什么?Dec 29, 2023 pm 02:27 PM
华为GT3 Pro和GT4的差异是什么?Dec 29, 2023 pm 02:27 PM许多用户在选择智能手表的时候都会选择的华为的品牌,其中华为GT3pro和GT4都是非常热门的选择,不少用户都很好奇华为GT3pro和GT4有什么区别,下面就就给大家介绍一下二者。华为GT3pro和GT4有什么区别一、外观GT4:46mm和41mm,材质是玻璃表镜+不锈钢机身+高分纤维后壳。GT3pro:46.6mm和42.9mm,材质是蓝宝石玻璃表镜+钛金属机身/陶瓷机身+陶瓷后壳二、健康GT4:采用最新的华为Truseen5.5+算法,结果会更加的精准。GT3pro:多了ECG心电图和血管及安
 C语言return的用法详解Oct 07, 2023 am 10:58 AM
C语言return的用法详解Oct 07, 2023 am 10:58 AMC语言return的用法有:1、对于返回值类型为void的函数,可以使用return语句来提前结束函数的执行;2、对于返回值类型不为void的函数,return语句的作用是将函数的执行结果返回给调用者;3、提前结束函数的执行,在函数内部,我们可以使用return语句来提前结束函数的执行,即使函数并没有返回值。
 修复:截图工具在 Windows 11 中不起作用Aug 24, 2023 am 09:48 AM
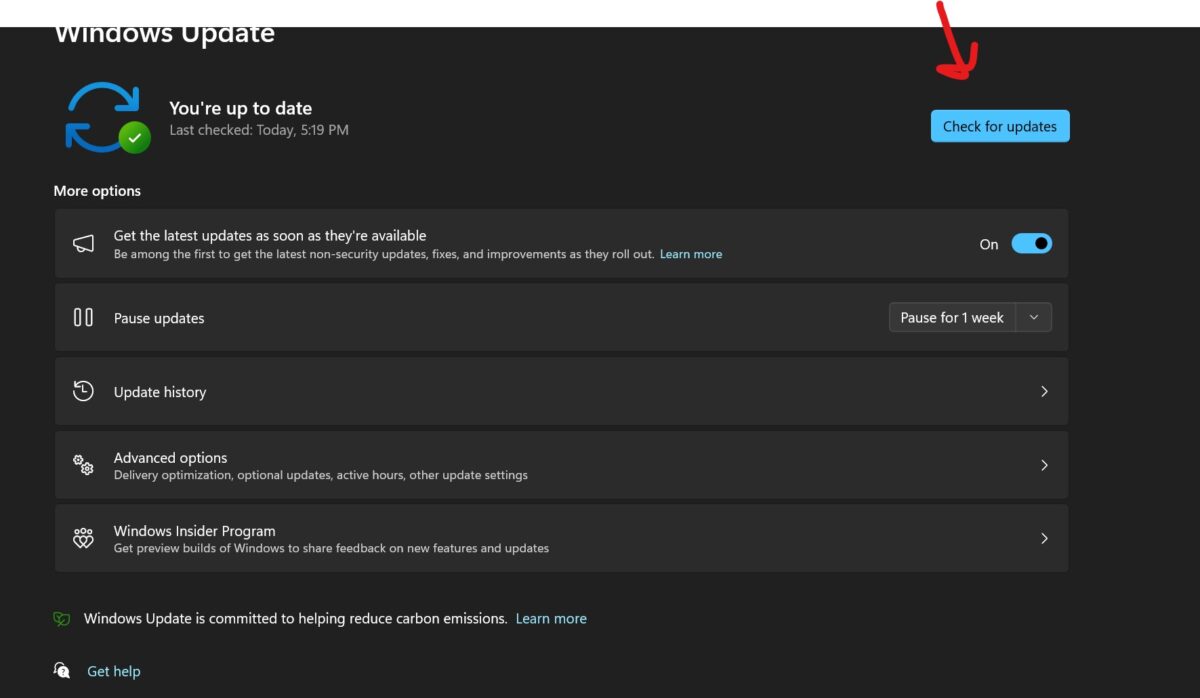
修复:截图工具在 Windows 11 中不起作用Aug 24, 2023 am 09:48 AM为什么截图工具在Windows11上不起作用了解问题的根本原因有助于找到正确的解决方案。以下是截图工具可能无法正常工作的主要原因:对焦助手已打开:这可以防止截图工具打开。应用程序损坏:如果截图工具在启动时崩溃,则可能已损坏。过时的图形驱动程序:不兼容的驱动程序可能会干扰截图工具。来自其他应用程序的干扰:其他正在运行的应用程序可能与截图工具冲突。证书已过期:升级过程中的错误可能会导致此issu简单的解决方案这些适合大多数用户,不需要任何特殊的技术知识。1.更新窗口和Microsoft应用商店应用程
 Java中return和finally语句的执行顺序是怎样的?Apr 25, 2023 pm 07:55 PM
Java中return和finally语句的执行顺序是怎样的?Apr 25, 2023 pm 07:55 PM源码:publicclassReturnFinallyDemo{publicstaticvoidmain(String[]args){System.out.println(case1());}publicstaticintcase1(){intx;try{x=1;returnx;}finally{x=3;}}}#输出上述代码的输出可以简单地得出结论:return在finally之前执行,我们来看下字节码层面上发生了什么事情。下面截取case1方法的部分字节码,并且对照源码,将每个指令的含义注释在
 PHP中int类型转换为字节的方法详解Mar 06, 2024 pm 06:18 PM
PHP中int类型转换为字节的方法详解Mar 06, 2024 pm 06:18 PMPHP中int类型转换为字节的方法详解在PHP中,我们经常需要将整数类型(int)转换为字节(Byte)类型,比如在处理网络数据传输、文件处理或者加密算法等场景中。本文将详细介绍如何将int类型转换为字节类型,以及提供具体的代码示例。1.int类型与字节的关系在计算机领域,基本数据类型int表示整数,而字节(Byte)是计算机存储单位,通常是8位二进制数据
 C++程序将double类型的变量转换为int类型Aug 25, 2023 pm 08:25 PM
C++程序将double类型的变量转换为int类型Aug 25, 2023 pm 08:25 PM在C++中,int类型的变量只能保存正整数或负整数值;它们不能保存小数值。有float和double值可用于此目的。为了存储小数点后最多七位的小数,创建了双精度数据类型。整数到双精度数据类型的转换可以由编译器自动完成(称为“隐式”转换),也可以由程序员向编译器显式请求(称为“显式”转换)。在接下来的部分中,我们将介绍各种转换方法。隐式转换编译器自动执行隐式类型转换。要实现这一点,需要两个变量——一个是浮点类型,另一个是整数类型。当我们简单地将浮点值或变量分配给整数变量时,编译器将处理所有其他事情
 如何修复无法连接到iPhone上的App Store错误Jul 29, 2023 am 08:22 AM
如何修复无法连接到iPhone上的App Store错误Jul 29, 2023 am 08:22 AM第1部分:初始故障排除步骤检查苹果的系统状态:在深入研究复杂的解决方案之前,让我们从基础知识开始。问题可能不在于您的设备;苹果的服务器可能会关闭。访问Apple的系统状态页面,查看AppStore是否正常工作。如果有问题,您所能做的就是等待Apple修复它。检查您的互联网连接:确保您拥有稳定的互联网连接,因为“无法连接到AppStore”问题有时可归因于连接不良。尝试在Wi-Fi和移动数据之间切换或重置网络设置(“常规”>“重置”>“重置网络设置”>设置)。更新您的iOS版本:
 int32的取值范围是多少Aug 11, 2023 pm 02:53 PM
int32的取值范围是多少Aug 11, 2023 pm 02:53 PMint32的取值范围是从-2的31次方到2的31次方减1,即-2147483648到2147483647。int32是有符号的整数类型,意味着它可以表示正数、负数和零,它使用1位来表示符号位,而剩余的31位用来表示数值。由于一位被用来表示符号位,所以int32的有效位数是31位。


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

ZendStudio 13.5.1 Mac
強力な PHP 統合開発環境

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

SecLists
SecLists は、セキュリティ テスターの究極の相棒です。これは、セキュリティ評価中に頻繁に使用されるさまざまな種類のリストを 1 か所にまとめたものです。 SecLists は、セキュリティ テスターが必要とする可能性のあるすべてのリストを便利に提供することで、セキュリティ テストをより効率的かつ生産的にするのに役立ちます。リストの種類には、ユーザー名、パスワード、URL、ファジング ペイロード、機密データ パターン、Web シェルなどが含まれます。テスターはこのリポジトリを新しいテスト マシンにプルするだけで、必要なあらゆる種類のリストにアクセスできるようになります。

ホットトピック
 7439
7439 15
15 1369
1369 52
52


