今回は部分適用について学びましょう。まず関数の概要を見てみましょう:
数学では、関数は各入力値と一意の出力値の間の対応関係を記述します。記号は f(x) です。たとえば、式 f(x)=x2 は、各入力値 x が固有の出力値 x2 に関連付けられている関数 f を表します。
つまり、入力値が 3 の場合、対応する出力値は 9 になります。また、 g(x,y) = xy には 2 つのパラメータ x と y があり、その積 xy が値になります。関数は上記で説明されています (便宜上、x と y が両方とも int であると仮定します)。f(x) を別の方法で表現できる例を 2 つ示します。 x2) 、つまり、 f を x2 にマッピングした後、 int -> int; と記述されます。
int を受け入れ、int を返します。 g(x,y) をもう一度見ると、 x -> y -> z(xy) と表すことができます。つまり、x、y は、int -> int -> int として記述され、z から g にマッピングされます。 g(x,y) 関数を見て、JavaScript を使用してそれを実装してみましょう:
function g(x,y){
return x*y;
}
これは完璧で、数学的定義に非常に近いです。 2 つのパラメータ x と y を順番に受け入れます。そして両者の積を返します。ただし、x=n (n は自然数) など、x が定数の場合。したがって、g(n,y)=ny となります。これは定数と変数の積となり、パラメーター y を受け取り ny を返します。つまり、int -> int と書かれた y -> z(ny) のマッピングになります。したがって、上記の作業は次のように理解できます。 g(x,y) はパラメータ int を受け入れ、関数 int ->int を返します。この返される関数は int のみを受け入れ、int を返します。これを JavaScript で表現してみましょう:
var h = g(2 );
h ここで、関数 h(y)=2y を表します。このようにして、h(5)=10、h(13)=26 などとなります。
h(5); (13) ;
varindex=index||0,args = new Array(a.length -index)
for(var i in a){
if(i> =index) args[i -index]=a[i];
}
return args;
function m(scope,fn){
if(arguments.lengthvar p = atarr(arguments,2);
var args = atarr(arguments);
return fn.apply(scope) ,p.concat(args ));
}
}
テストコード:
console.log(plus2(10));
//結果
12
これが私たちの目標であり、実装されました。上記の atarr 関数は、arguments オブジェクト内の指定された位置から始まるパラメーターを取り出し、配列に保存します。 m 関数が主役で、以前に定義したタスクを完了し、関数チェーン上のパラメーターを保存し、残りのパラメーターを受け入れる関数を返します。テスト コードの plus 関数は、もともと 2 つのパラメーター a と b を受け入れ、a と b の合計を返しました。ただし、plus2 は 1 つのパラメーター b を受け入れ、それを 2 に加算します。 2 と b の合計は int -> int を返します。
上記の作業の一部を通じて、JavaScript で部分アプリケーションを実装し、hitch2 で Dojo フレームワークにドメイン バインディングと部分を実装しました。興味があれば、そのソース コードを読んでみてください。これも非常にシンプルで明確です。
 JavaScriptの文字列文字を交換しますMar 11, 2025 am 12:07 AM
JavaScriptの文字列文字を交換しますMar 11, 2025 am 12:07 AMJavaScript文字列置換法とFAQの詳細な説明 この記事では、javaScriptの文字列文字を置き換える2つの方法について説明します:内部JavaScriptコードとWebページの内部HTML。 JavaScriptコード内の文字列を交換します 最も直接的な方法は、置換()メソッドを使用することです。 str = str.replace( "find"、 "置換"); この方法は、最初の一致のみを置き換えます。すべての一致を置き換えるには、正規表現を使用して、グローバルフラグGを追加します。 str = str.replace(/fi
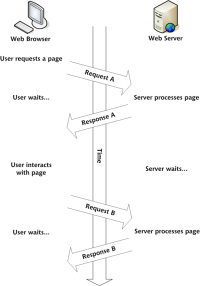 独自のAjax Webアプリケーションを構築しますMar 09, 2025 am 12:11 AM
独自のAjax Webアプリケーションを構築しますMar 09, 2025 am 12:11 AMそれで、あなたはここで、Ajaxと呼ばれるこのことについてすべてを学ぶ準備ができています。しかし、それは正確には何ですか? Ajaxという用語は、動的でインタラクティブなWebコンテンツを作成するために使用されるテクノロジーのゆるいグループ化を指します。 Ajaxという用語は、もともとJesse Jによって造られました
 10 jQueryの楽しみとゲームプラグインMar 08, 2025 am 12:42 AM
10 jQueryの楽しみとゲームプラグインMar 08, 2025 am 12:42 AM10の楽しいjQueryゲームプラグインして、あなたのウェブサイトをより魅力的にし、ユーザーの粘着性を高めます! Flashは依然としてカジュアルなWebゲームを開発するのに最適なソフトウェアですが、jQueryは驚くべき効果を生み出すこともできます。また、純粋なアクションフラッシュゲームに匹敵するものではありませんが、場合によってはブラウザで予期せぬ楽しみもできます。 jquery tic toeゲーム ゲームプログラミングの「Hello World」には、JQueryバージョンがあります。 ソースコード jQueryクレイジーワードコンポジションゲーム これは空白のゲームであり、単語の文脈を知らないために奇妙な結果を生み出すことができます。 ソースコード jquery鉱山の掃引ゲーム
 独自のJavaScriptライブラリを作成および公開するにはどうすればよいですか?Mar 18, 2025 pm 03:12 PM
独自のJavaScriptライブラリを作成および公開するにはどうすればよいですか?Mar 18, 2025 pm 03:12 PM記事では、JavaScriptライブラリの作成、公開、および維持について説明し、計画、開発、テスト、ドキュメント、およびプロモーション戦略に焦点を当てています。
 jQuery Parallaxチュートリアル - アニメーションヘッダーの背景Mar 08, 2025 am 12:39 AM
jQuery Parallaxチュートリアル - アニメーションヘッダーの背景Mar 08, 2025 am 12:39 AMこのチュートリアルでは、jQueryを使用して魅惑的な視差の背景効果を作成する方法を示しています。 見事な視覚的な深さを作成するレイヤー画像を備えたヘッダーバナーを構築します。 更新されたプラグインは、jQuery 1.6.4以降で動作します。 ダウンロードしてください
 ブラウザでのパフォーマンスのためにJavaScriptコードを最適化するにはどうすればよいですか?Mar 18, 2025 pm 03:14 PM
ブラウザでのパフォーマンスのためにJavaScriptコードを最適化するにはどうすればよいですか?Mar 18, 2025 pm 03:14 PMこの記事では、ブラウザでJavaScriptのパフォーマンスを最適化するための戦略について説明し、実行時間の短縮、ページの負荷速度への影響を最小限に抑えることに焦点を当てています。
 Matter.jsを始めましょう:はじめにMar 08, 2025 am 12:53 AM
Matter.jsを始めましょう:はじめにMar 08, 2025 am 12:53 AMMatter.jsは、JavaScriptで書かれた2D Rigid Body Physics Engineです。このライブラリは、ブラウザで2D物理学を簡単にシミュレートするのに役立ちます。剛体を作成し、質量、面積、密度などの物理的特性を割り当てる機能など、多くの機能を提供します。また、重力摩擦など、さまざまな種類の衝突や力をシミュレートすることもできます。 Matter.jsは、すべての主流ブラウザをサポートしています。さらに、タッチを検出し、応答性が高いため、モバイルデバイスに適しています。これらの機能はすべて、物理ベースの2Dゲームまたはシミュレーションを簡単に作成できるため、エンジンの使用方法を学ぶために時間をかける価値があります。このチュートリアルでは、このライブラリのインストールや使用法を含むこのライブラリの基本を取り上げ、
 jqueryとajaxを使用した自動更新DivコンテンツMar 08, 2025 am 12:58 AM
jqueryとajaxを使用した自動更新DivコンテンツMar 08, 2025 am 12:58 AMこの記事では、JQueryとAjaxを使用して5秒ごとにDivのコンテンツを自動的に更新する方法を示しています。 この例は、RSSフィードからの最新のブログ投稿と、最後の更新タイムスタンプを取得して表示します。 読み込み画像はオプションです


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 中国語版
中国語版、とても使いやすい

MinGW - Minimalist GNU for Windows
このプロジェクトは osdn.net/projects/mingw に移行中です。引き続きそこでフォローしていただけます。 MinGW: GNU Compiler Collection (GCC) のネイティブ Windows ポートであり、ネイティブ Windows アプリケーションを構築するための自由に配布可能なインポート ライブラリとヘッダー ファイルであり、C99 機能をサポートする MSVC ランタイムの拡張機能が含まれています。すべての MinGW ソフトウェアは 64 ビット Windows プラットフォームで実行できます。

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

メモ帳++7.3.1
使いやすく無料のコードエディター

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

ホットトピック
 7417
7417 15
15 1359
1359 52
52


