PHPマスター| PHP開発のデータ構造：グラフ

キーテイクアウト

• グラフは、キー/バリューのペア間の関係をモデル化するために使用される数学的構成であり、ネットワークの最適化、トラフィックルーティング、ソーシャルネットワーク分析などの多くの実際のアプリケーションを持っています。それらは、それらを接続する頂点（ノード）とエッジ（線）で構成されています。これらは、指示または無向、および重み付けまたは加重されていません。
グラフは、隣接マトリックスまたは隣接リストとして2つの方法で表現できます。隣接リストは、特に頂点のほとんどのペアが接続されていないスパースグラフの場合、より空間効率が高くなりますが、隣接するマトリックスはより迅速な検索を容易にします。
• グラフ理論の一般的なアプリケーションは、任意の2つのノードの間でホップの最小数（つまり、最短パス）を見つけることです。これは、指定されたルートノードからレベルごとにグラフレベルを通過することを含む幅最初の検索を使用して実現できます。このプロセスでは、訪問されていないノードのキューを維持する必要があります
dijkstraのアルゴリズムは、グラフ内の任意の2つのノード間の最短または最も最適なパスを見つけるために広く使用されています。これには、ソースノードから始まるすべての頂点のすべての可能な頂点間の各エッジを調べ、ターゲットノードに到達するまで最短合計距離で更新された頂点セットを維持することが含まれます。

以前の記事の1つで、ツリーデータ構造を紹介しました。次に、関連する構造 - グラフを探りたいと思います。グラフには、ネットワークの最適化、トラフィックルーティング、ソーシャルネットワーク分析など、多くの実際のアプリケーションがあります。 GoogleのPageRank、Facebookのグラフ検索、AmazonとNetflixの推奨事項は、グラフ駆動型アプリケーションの例です。 この記事では、グラフが使用される2つの一般的な問題、つまりホップ数と最短の問題を調査します。 グラフは、キー/値のペア間の関係をモデル化するために使用される数学的構成要素です。グラフは、それらを接続する頂点（ノード）のセットと任意の数のエッジ（行）を含む。これらのエッジは、指示または無向にできます。指向されたエッジは、単に2つの頂点の間のエッジであり、エッジA→BはB→Aと同じとは見なされません。無向エッジには方向や方向がありません。エッジA-BはB-Aに相当します。前回について学んだツリー構造は、無視されていないグラフの一種と見なすことができ、各頂点は単純なパスによって少なくとも1つの他の頂点に接続されています。 グラフは加重または加重されていない場合もあります。加重グラフ、またはネットワークは、そのエッジの各エッジに重みまたはコスト値が割り当てられるものです。加重グラフは、2つのポイント間の最も最適なパス、最も便利な、または最低の「コスト」パスを決定する際に一般的に使用されます。 GoogleMapの運転指示は、加重グラフを使用する例です。

ホップの最小数

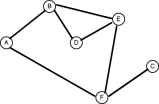
グラフ理論の一般的なアプリケーションは、任意の2つのノードの間で最も少ないホップ数を見つけることです。木と同様に、グラフは、深さfirstまたは幅の2つの方法のいずれかで通過できます。前の記事では深さ最初の検索について説明したので、幅広い最初の検索を見てみましょう。 次のグラフを検討してください。

簡単にするために、グラフが無向であると仮定しましょう。つまり、任意の方向のエッジが同一であると仮定します。私たちのタスクは、任意の2つのノードの間にホップ数が少ないことを見つけることです。 幅最初の検索では、ルートノード（またはルートとして指定されたノード）から開始し、レベルごとにツリーを下に向けます。それを行うには、各レベルの後にバックトラックして処理できるように、視界のないノードのリストを維持するためのキューが必要です。 一般的なアルゴリズムは次のようになります。

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

しかし、最初にグラフを横断せずに、どのノードが隣接しているかは言うまでもなく、どのようにしても、どのノードが隣接しているかをどのようにして知るのでしょうか？これにより、グラフデータ構造をどのようにモデル化できるかという問題が発生します。 グラフを表す

通常、グラフを表すには2つの方法があります。隣接マトリックスまたは隣接リストのいずれかです。隣接リストとして表される上記のグラフは、次のようになります。

マトリックスとして表されるグラフは次のようになります。1つは、2つの頂点の間のエッジの「発生率」を示します。

隣接リストは、特に頂点のほとんどのペアが接続されていないスパースグラフでは、より空間効率が高くなりますが、隣接するマトリックスはより迅速な検索を容易にします。最終的に、表現の選択は、どのタイプのグラフ操作が必要であるかによって異なります。 グラフを表すために隣接リストを使用しましょう。

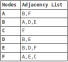
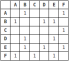
1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

そして今、一般的な幅広い検索アルゴリズムの実装がどのように見えるかを見てみましょう。

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

次の例を実行すると、次のようになります。

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

キューの代わりにスタックを使用していた場合、トラバーサルは深度最初の検索になります。

最短パス

を見つける もう1つの一般的な問題は、任意の2つのノード間で最も最適なパスを見つけることです。以前、私はこの例として、GoogleMapの運転指示について言及しました。その他のアプリケーションには、旅行の旅程の計画、道路交通管理、列車/バスのスケジューリングが含まれます。 この問題に対処するための最も有名なアルゴリズムの1つは、1959年にEdsger W. Dijkstraという名前の29歳のコンピューター科学者によって発明されました。一般的に、Dijkstraのソリューションでは、ソースノードから始まるすべての頂点のすべての可能な頂点間の各エッジを調べ、ターゲットノードに到達するか、到達しないまでの最短総距離で頂点の更新セットを維持することが含まれます。 ソリューションを実装するにはいくつかの方法があります。実際、1959年にわたって長年にわたり、ミニホープ、優先順位、フィボナッチヒープを使用して、Dijkstraの元のアルゴリズムに多くの多くの機能が作成されました。パフォーマンスが向上したものもあれば、Dijkstraのソリューションの欠点に対処するように設計されたものもあります。 （正の）加重グラフの例は次のとおりです。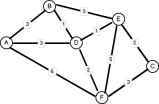

次のように、このグラフを隣接リストとして表すことができます。

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

そして、PriorityQueueを使用した実装を使用して、すべての「最適化されていない」頂点のリストを維持します。

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

ご覧のとおり、Dijkstraのソリューションは、単に幅広い最初の検索のバリエーションです！ 次の例を実行すると、次の結果が得られます。

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

要約

この記事では、グラフ理論の基本、グラフを表す2つの方法、およびグラフ理論の適用における2つの根本的な問題を紹介しました。 2つのノード間のホップ数が少ないために幅広い検索を使用して、Dijkstraのソリューションを使用して2つのノード間で最も短いパスを見つける方法を示しました。 Fotoliaを介した画像 データ構造のグラフに関するよくある質問（FAQ）

データ構造内のグラフとツリーの違いは何ですか？

グラフとツリーはどちらも非線形データ構造ですが、いくつかの重要な違いがあります。ツリーはグラフの一種ですが、すべてのグラフがツリーではありません。ツリーは、サイクルのない接続されたグラフです。ルートノードとチャイルドノードを備えた階層構造があります。ツリー内の各ノードには、ルートから一意のパスがあります。一方、グラフにはサイクルがあり、その構造はより複雑です。接続または切断することができ、ノードはそれらの間に複数のパスを持つことができます。

データ構造でグラフはどのように表されますか？リスト。隣接するマトリックスは、v x vの2D配列です。ここで、vはグラフの頂点の数です。頂点IとJの間にエッジがある場合、行Iと列jの交差点のセルは1、そうでない場合は0になります。隣接リストはリンクリストの配列です。配列のインデックスは頂点を表し、リンクリストの各要素は、頂点とともにエッジを形成する他の頂点を表します。データ構造のいくつかのタイプのグラフです。単純なグラフは、ループがなく、2つの頂点の間に1つしかエッジ以下のグラフです。マルチグラフは、頂点間に複数のエッジを持つことができます。完全なグラフは、すべてのペアの頂点がエッジによって接続されている単純なグラフです。加重グラフは、各エッジに重量を割り当てます。指示されたグラフ（またはgigraph）には、方向のあるエッジがあります。エッジは、ある頂点から別の頂点まで指さします

コンピューターサイエンスにおけるグラフのアプリケーションは何ですか？

グラフは、コンピューターサイエンスの多数のアプリケーションで使用されています。それらは、人々の間のつながりを表すためにソーシャルネットワークで使用されます。 Webクロールで使用され、Webページにアクセスして検索インデックスを作成します。 2つのノード間の最適なパスを見つけるために、ネットワークルーティングアルゴリズムで使用されます。それらは生物学で使用され、生物学的ネットワークをモデル化および分析します。また、コンピューターのグラフィックスと物理シミュレーションでも使用されています。

グラフトラバーサルアルゴリズムは何ですか？

2つの主要なグラフトラバーサルアルゴリズムがあります。 （BFS）。 DFSは、バックトラッキングの前に各ブランチに沿って可能な限り探索します。スタックデータ構造を使用します。 BFSは、次のレベルに進む前に、現在の深さですべての頂点を調査します。キューデータ構造を使用しています。

java？

にグラフを実装する方法Javaでは、ハッシュマップを使用して隣接するリストを保存するグラフを実装できます。ハッシュマップの各キーは頂点であり、その値は、それが接続されている頂点を含むLinkedListです。すべてのエッジが1つのセットの頂点を他のセットの頂点に接続するように、2つの分離セットに分割されます。同じセット内の頂点を接続するエッジはありません。

サブグラフとは何ですか？

サブグラフは、別のグラフの一部であるグラフです。元のグラフの（またはすべての）頂点と元のグラフのいくつかの（またはすべての）エッジがあります。

グラフのサイクルは何ですか？同じ頂点で開始および終了し、少なくとも1つのエッジを持つパス。グラフ内のパスとは

グラフ内のパスは、各ペアが頂点のシーケンスであり、の連続した頂点は、エッジによって接続されています

以上がPHPマスター| PHP開発のデータ構造：グラフの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。