Big-O 表記の簡略化: アルゴリズム効率のガイド |ブログ

Big O Notation を理解する: アルゴリズム効率に関する開発者ガイド

ソフトウェア開発者として、Web アプリケーション、モバイル アプリケーションを構築しているか、データ処理を処理しているかに関係なく、Big O 表記法を理解することは不可欠です。 これはアルゴリズムの効率を評価するための鍵であり、アプリケーションのパフォーマンスとスケーラビリティに直接影響します。 Big O を理解すればするほど、コードの最適化がより上手になります。

このガイドでは、Big O 表記法、その重要性、時間と空間の複雑さに基づいてアルゴリズムを分析する方法について徹底的に説明します。完全な理解を提供するために、コーディング例、実際のアプリケーション、および高度な概念を取り上げます。

目次

1. Big O 記法とは何ですか?
2. なぜ Big O 表記が重要ですか?
3. 主要な Big O 表記
4. 先進的な Big O コンセプト
5. Big O 記法の現実世界への応用
6. アルゴリズムの最適化: 実用的なソリューション
7. 結論
8. よくある質問 (FAQ)

Big O 記法とは何ですか?

Big O 記法は、アルゴリズムのパフォーマンスや複雑さを記述するための数学的ツールです。 具体的には、入力サイズの増加に応じてアルゴリズムの実行時間またはメモリ使用量がどのようにスケールされるかを示します。 Big O を理解すると、アルゴリズムが大規模なデータセットでどのように動作するかを予測できます。

なぜ Big O 表記が重要ですか?

何百万ものユーザーと投稿を処理する必要があるソーシャル メディア プラットフォームを考えてみましょう。最適化されたアルゴリズム (Big O を使用して分析) がなければ、ユーザー数が増加するにつれてプラットフォームが遅くなったり、クラッシュしたりする可能性があります。 Big O は、入力サイズ (ユーザーや投稿など) の増加に伴うコードのパフォーマンスを予測するのに役立ちます。

• Big O がなければ、コード最適化の方向性が欠けてしまいます。
• Big O を使用すると、大規模なデータセットであってもスケーラブルで効率的なアルゴリズムを設計できます。

主要な Big O 表記

1. 定数時間: O(1)

O(1) アルゴリズムは、入力サイズに関係なく、固定数の演算を実行します。 入力が増加しても実行時間は一定のままです。

例: 最初の配列要素を取得する関数:

<code class="language-javascript">function getFirstElement(arr) {
  return arr[0];
}</code>

配列サイズに関係なく、実行時間は一定です – O(1)。

現実世界のシナリオ: 自動販売機がスナックを供給するのにかかる時間は、入手可能なスナックの数に関係なく同じです。

2. 対数時間: O(log n)

対数的な時間計算量は、アルゴリズムが反復ごとに問題のサイズを半分にするときに発生します。これにより、複雑さは O(log n) になります。つまり、実行時間は入力サイズに応じて対数的に増加します。

例: 二分探索は典型的な例です:

<code class="language-javascript">function getFirstElement(arr) {
  return arr[0];
}</code>

反復ごとに検索スペースが半分になり、結果は O(log n) になります。

現実世界のシナリオ: 並べ替えられた電話帳で名前を見つける。

3. 線形時間: O(n)

O(n) の複雑さは、実行時間が入力サイズに正比例して増大することを意味します。 要素を 1 つ追加すると、実行時間が一定量増加します。

例: 配列内の最大要素の検索:

<code class="language-javascript">function binarySearch(arr, target) {
  let low = 0;
  let high = arr.length - 1;

  while (low <= high) {
    let mid = Math.floor((low + high) / 2);
    if (arr[mid] === target) {
      return mid;
    } else if (arr[mid] < target) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }
  return -1; // Target not found
}</code>

アルゴリズムは各要素を 1 回反復処理します – O(n)。

現実世界のシナリオ: 人の列を 1 人ずつ処理します。

4. 線形時間: O(n log n)

O(n log n) は、マージ ソートやクイック ソートなどの効率的な並べ替えアルゴリズムで一般的です。 彼らは入力をより小さな部分に分割し、効率的に処理します。

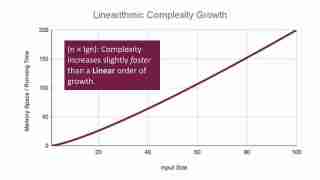
例: ソートのマージ (簡潔にするために実装は省略)。 配列を再帰的に分割 (log n) し、結合 (O(n)) し、結果は O(n log n) になります。

現実世界のシナリオ: 大人数のグループを身長順に並べ替えます。

5. 二次時間: O(n²)

O(n²) アルゴリズムには通常、ネストされたループがあり、1 つのループ内の各要素が別のループ内のすべての要素と比較されます。

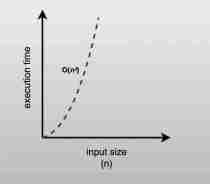
例: バブルソート (簡潔にするために実装は省略)。 ネストされたループは O(n²) につながります。

現実世界のシナリオ: グループ内の全員の身長と他の全員の身長を比較します。

6. 立方時間: O(n³)

3 つのネストされたループを含むアルゴリズムの複雑さは、多くの場合 O(n³) です。これは、行列のような多次元データ構造を扱うアルゴリズムでは一般的です。

例: 3 つのネストされたループを使用した単純な行列の乗算 (簡潔にするために実装は省略) の結果は O(n³) になります。

現実世界のシナリオ: グラフィックス プログラムで 3D オブジェクトを処理します。

先進的な Big O コンセプト

1. 償却時間計算量: アルゴリズムには時折高価な操作が含まれる可能性がありますが、多くの操作の平均コストは低くなります (例: 動的な配列のサイズ変更)。

2. 最良、最悪、平均的なケース: Big O は多くの場合、最悪のシナリオを表します。 ただし、最良の場合 (Ω)、最悪の場合 (O)、および平均的な場合 (Θ) の複雑さにより、より完全な全体像が得られます。

3. 空間の複雑さ: Big O はアルゴリズムのメモリ使用量 (空間の複雑さ) も分析します。 時間と空間の両方の複雑さを理解することは、最適化にとって非常に重要です。

結論

このガイドでは、基本的な概念から高度な概念まで Big O 記法について説明しました。 Big O 分析を理解して適用することで、より効率的でスケーラブルなコードを作成できます。 これを継続的に練習すると、より熟練した開発者になれます。

よくある質問 (FAQ)

• Big O 表記とは何ですか? 入力サイズの増加に伴うアルゴリズムのパフォーマンス (時間と空間) の数学的記述です。
• Big O はなぜ重要ですか? Big O は、コードのスケーラビリティと効率性の最適化に役立ちます。
• 最良、最悪、平均的なケースの違いは? 最良は最速、最悪は最も遅く、平均は期待されるパフォーマンスです。
• 時間と空間の複雑さ? 時間は実行時間を測定します。スペースはメモリ使用量を測定します。
• Big O を使用して最適化するにはどうすればよいですか? 複雑さを分析し、キャッシュや分割統治などの手法を使用します。
• 最適な並べ替えアルゴリズム? マージ ソートとクイック ソート (O(n log n)) は、大規模なデータセットに対して効率的です。
• ビッグ オーは時間と空間の両方に使用できますか? はい。

(注: 画像は存在し、元の​​入力どおりに正しくリンクされていると想定されています。わかりやすくするためにコード例は簡略化されています。より堅牢な実装が存在する可能性があります。)

以上がBig-O 表記の簡略化: アルゴリズム効率のガイド |ブログの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。