ホームページ >バックエンド開発 >Python チュートリアル >バッチ、ミニバッチ、確率的勾配降下法
バッチ、ミニバッチ、確率的勾配降下法
- Linda Hamiltonオリジナル
- 2024-11-24 11:26:09538ブラウズ
コーヒー買ってきて☕
*メモ:
- 私の投稿では、PyTorch の DataLoader() を使用したバッチ、ミニバッチ、確率的勾配降下法について説明しています。
- 私の投稿では、PyTorch で DataLoader() を使用しないバッチ勾配降下法について説明しています。
- 私の投稿では、PyTorch のオプティマイザーについて説明しています。
バッチ勾配降下法(BGD)、ミニバッチ勾配降下法(MBGD)、確率的勾配降下法(SGD)があり、これらはデータセットからデータを取得する方法を使用して勾配降下法を実行する方法です。 Adam()、SGD()、RMSprop()、Adadelta()、Adagrad() などのオプティマイザPyTorch.
*メモ:
- PyTorch の SGD() は、特別な機能のない単なる基本的な勾配降下法 (クラシック勾配降下法(CGD)) ですが、確率的勾配降下法(SGD) ではありません。
- たとえば、以下の方法を使用すると、Adam() で BGD、MBGD、または SGD Adam、SGD() で CGD、RMSprop() で RMSprop、Adadelta() で Adadelta、Adagrad() で Adagrad を柔軟に実行できます。 PyTorch など。
- 基本的に、BGD、MBGD、または SGD は、DataLoader() を使用してシャッフルされたデータセットを使用して実行されます。
*メモ:
- データセットをシャッフルすると、過学習が軽減されます。 ※基本的にはトレーニングデータのみをシャッフルするため、テストデータはシャッフルされません。
- 私の投稿では、過学習と過小学習について説明しています。
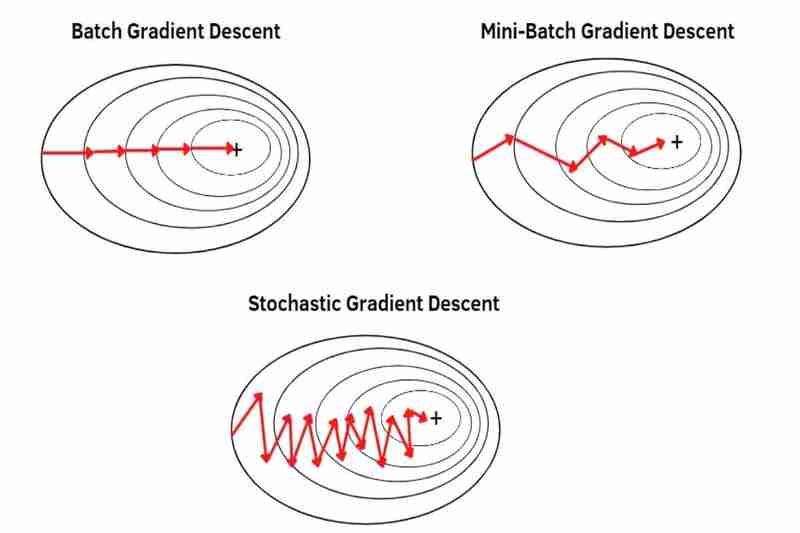
(1) バッチ勾配降下法(BGD):
- は、データセット全体に対して勾配降下を実行でき、1 エポックで 1 ステップのみ実行します。たとえば、データセット全体に 100 サンプル (1x100) がある場合、勾配降下法は 1 エポックで 1 回だけ発生します。これは、モデルのパラメーターが 1 エポックで 1 回だけ更新されることを意味します。
- はデータセット全体の平均を使用するため、各サンプルはMBGDやSGDよりも目立たなくなります(あまり強調されません)。その結果、MBGD や SGD よりも収束が安定し (変動が少ない)、MBGD や SGD よりもノイズ (ノイズの多いデータ) にも強いため、MBGD や SGD よりもオーバーシュートが少なく、次の場合に MBGD や SGD よりも正確なモデルを作成できます。極小値にはまり込んでいませんが、MBGD や SGD よりも収束が安定している (変動が少ない) ため、BGD は MBGD や SGD よりも極小値や鞍点から脱出しにくいです。前にも言いましたが、BGD は MBGD や SGD よりも各サンプルが目立たない(強調されない)ため、MBGD や SGD よりも過学習を引き起こしやすくなります。
*メモ:
- 収束 は、初期重みが勾配降下法によって関数の大域最小値に向かって移動することを意味します。
- ノイズ (ノイズのあるデータ) は、外れ値、異常、または場合によっては重複するデータを意味します。
- オーバーシュートとは、関数のグローバル最小値を飛び越えることを意味します。
- の長所:
- MBGD や SGD よりも収束が安定しています (変動が少ない)。
- MBGDやSGDよりもノイズ(ノイズの多いデータ)に強いです。
- MBGD や SGD よりもオーバーシュートの発生が少なくなります。
- 極小値にとらわれなければ、MBGD や SGD よりも正確なモデルが作成されます。
- の短所:
- オンライン学習などの大規模なデータセットは多くのメモリを必要とし、収束が遅くなるため苦手です。 *オンライン学習は、モデルがリアルタイムでデータセットのストリームから段階的に学習する方法です。
- モデルを更新したい場合は、データセット全体を再準備する必要があります。
- MBGD や SGD よりも局所最小値または鞍点から逃れるのが難しくなります。
- MBGD や SGD よりも簡単に過学習が発生します。
(2) ミニバッチ勾配降下法(MBGD):
- 分割されたデータセット (データセット全体の小さなバッチ) を 1 つの小さなバッチずつ使用して勾配降下を実行でき、1 エポック内のデータセット全体の小さなバッチと同じステップ数を実行します。たとえば、100 個のサンプル (1x100) を持つデータセット全体が 5 つの小さなバッチ (5x20) に分割され、勾配降下が 1 エポックで 5 回発生します。これは、モデルのパラメーターが 1 エポックで 5 回更新されることを意味します。
は、データセット全体から分割された各小さなバッチの平均を使用するため、BDG よりも各サンプルがより目立つ(より強調される)ようになります。 *データセット全体を小さなバッチに分割すると、各サンプルがますます目立つようになります (ますます強調されます)。その結果、BGD よりも収束が安定せず (変動が多く)、BGD よりもノイズ (ノイズの多いデータ) に強くないため、BGD よりもオーバーシュートが発生し、極小値にはまらなかったとしても BGD よりも精度の低いモデルが作成されます。前に述べたように、MBGD は BGD よりも収束が安定していない (変動が大きい) ため、BGD よりも局所最小値または鞍点から脱出しやすく、MBGD は BGD よりも過学習を引き起こしにくいためです。先ほども言いましたが、サンプルはBGDよりも目立ちます(強調されます)。
-
の長所:
- オンライン学習などの大規模なデータセットでは BGD よりも優れています。BGD よりも必要なメモリが少なく、BGD よりも収束の速度が低下しないためです。
- モデルを更新する場合、データセット全体を再準備する必要はありません。
- BGD よりも簡単に極小値または鞍点を回避します。
- BGD よりも過剰適合が起こりにくくなります。
-
の短所:
- 収束は BGD よりも不安定です (変動が大きい)。
- BGD よりもノイズ (ノイズの多いデータ) に強くありません。
- BGD よりもオーバーシュートの原因となります。
- 極小値にとらわれていない場合でも、BGD よりも精度の低いモデルが作成されます。
(3) 確率的勾配降下法(SGD):
- は、データセット全体のすべてのサンプルを 1 サンプルずつ使用して、1 エポック内のデータセット全体のサンプルと同じ数のステップを実行して勾配降下を実行できます。たとえば、データセット全体に 100 個のサンプル (1x100) がある場合、勾配降下法は 1 エポックで 100 回発生します。これは、モデルのパラメーターが 1 エポックで 100 回更新されることを意味します。
はデータセット全体のすべての単一サンプルを1サンプルずつ使用しますが、平均は使用しないため、MBGDよりも各サンプルがより際立っています(より強調されています)。結果として、MBGD よりも収束が安定せず (変動が多く)、MBGD よりもノイズ (ノイズの多いデータ) に強くないため、MBGD よりもオーバーシュートが発生し、極小値に引っかかっていない場合でも MBGD より精度の低いモデルが作成されます。 SGD は、MBGD よりも局所最小値または鞍点から容易に脱出できます。これは、前に述べたように、収束が MBGD よりも安定していない (変動が大きい) ためであり、SGD は MBGD よりも過学習を引き起こしにくいためです。先ほども言いましたが、サンプルはMBGDよりも目立ちます(強調されます)。
-
の長所:
- MBGD よりも必要なメモリが少なく、MBGD よりも収束の速度が低下しないため、オンライン学習などの大規模なデータセットに適しています。
- モデルを更新する場合、データセット全体を再準備する必要はありません。
- MBGD よりも局所最小値または鞍点を簡単に回避できます。
- MBGD よりも過剰適合が起こりにくくなります。
-
の短所:
- 収束は MBGD よりも不安定です (変動が大きくなります)。
- MBGD よりもノイズ (ノイズの多いデータ) に強くありません。
- MBGD よりもオーバーシュートが発生します。
- 極小値にとらわれない場合、MBGD よりも精度の低いモデルが作成されます。
以上がバッチ、ミニバッチ、確率的勾配降下法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

