ホームページ >ウェブフロントエンド >jsチュートリアル >マージソートアルゴリズムを理解する: ソートアルゴリズムをマスターするための初心者向けガイド
マージソートアルゴリズムを理解する: ソートアルゴリズムをマスターするための初心者向けガイド
- Susan Sarandonオリジナル
- 2024-11-08 08:01:02696ブラウズ
これまでの記事では、バブル ソート、選択ソート、挿入ソートなど、多数のソート アルゴリズムについて学びました。これらの並べ替えアルゴリズムは実装が非常に簡単ですが、大規模なデータセットに対しては効率的ではないことがわかりました。つまり、大規模なデータセットの並べ替えを処理するには、より効率的なアルゴリズムが必要であるため、マージ ソートが必要になります。このシリーズでは、マージ ソートの仕組みと、それを JavaScript で実装する方法について説明します。準備はできていますか?

目次
- マージソートアルゴリズムとは何ですか?
-
マージソートアルゴリズムの仕組み
- 時間計算量
- 空間の複雑さ
- JavaScript での実装
- 結論
マージソートアルゴリズムとは何ですか?
マージ ソート アルゴリズム は、分割統治の原則に従った優れたソート アルゴリズムです。隣接する要素を比較する配列を複数回通過させる選択ソートやバブル ソートのような単純なアルゴリズムとは異なり、マージ ソートはより戦略的なアプローチを採用します。
- Divide: まず、マージソートにより配列を 2 つの半分に分割します
- 征服: 次に、各半分を再帰的にソートします
- 結合: 最後に、ソートされた半分を結合して戻します
このアプローチは、大規模なデータセットを扱う場合、選択ソートやバブルソートなどの単純な O(n²) アルゴリズムよりも常に優れています。
マージソートアルゴリズムの仕組み
マージソートは、一般的な分割統治アプローチを使用して機能することがわかりました。以下は、その仕組みを視覚的に表したものです。
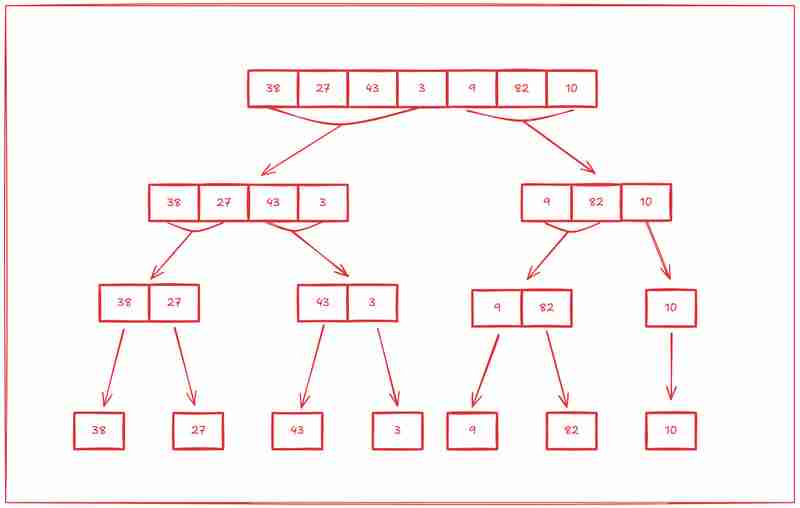
魔法を理解したので、上記のアプローチを使用してこの配列 [38, 27, 43, 3, 9, 82, 10] を手動で並べ替えることにより、マージ ソート アルゴリズムがどのように機能するかを見てみましょう。
ステップ 1: 分割する
マージソートの最初のステップは、配列をサブ配列に分割し、次に各サブ配列をサブ配列に分割し、すべてのサブ配列に項目が 1 つだけ残るまで、サブ配列をサブ配列に分割します。
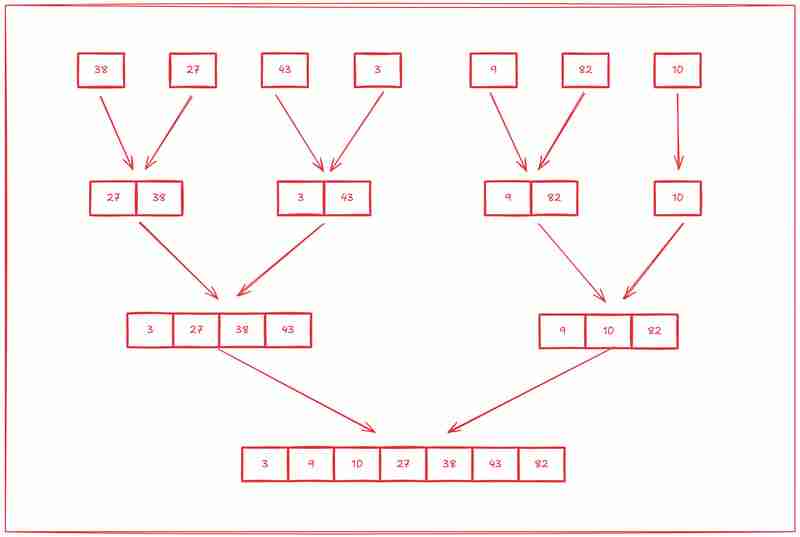
ステップ 2: マージバック (征服)
2 番目のステップは、これらのサブ配列を最初から並べ替えることです。
時間計算量
マージ ソートは、すべてのケース (最良、平均、最悪) で O(n log n) の時間計算量を実現し、大規模なデータセットの場合は O(n²) アルゴリズムより効率的です。
その理由は次のとおりです:
- 除算: 配列は log n 回分割されます (分割するたびにサイズが半分になります)
- マージ: マージの各レベルには n 個の操作が必要です
- 合計: n オペレーション × log n レベル = O(n log n)
これを次と比較してください:
- バブルソート: O(n²)
- 選択ソート: O(n²)
- マージソート: O(n log n)
1,000 要素の配列の場合:
- O(n²) ≈ 1,000,000 オペレーション
- O(n log n) ≈ 10,000 オペレーション
空間の複雑さ
マージ ソートには、マージ中に一時配列を保存するために O(n) 個の追加スペースが必要です。これはバブル ソートや選択ソートに必要な O(1) スペースよりも大きくなりますが、時間効率を考えれば、実際にはこのトレードオフに価値があるのが通常です。
JavaScriptでの実装
// The Merge Helper Function
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// Add remaining elements
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
while (rightIndex < right.length) {
result.push(right[rightIndex]);
rightIndex++;
}
return result;
}
マージ関数の詳細:
- 機能設定:
const result = []; let leftIndex = 0; let rightIndex = 0;
- マージされた結果を保存する空の配列を作成します
- 両方の入力配列のポインターを初期化します
- これらのポインターは、各配列内のどこにいるかを追跡する指のようなものだと考えてください
- メインのマージロジック:
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
- 両方の配列の要素を比較します
- 小さい方の要素を取得して結果に追加します
- 取得した配列内でポインタを前方に移動します
- デッキを並べ替えるときに 2 枚のカードのうち小さい方を選ぶのと同じです
- クリーンアップフェーズ:
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
- 残りの要素を追加します
- 一方の配列が他方の配列よりも長い可能性があるため必要です
- 比較して残ったカードを集める感じ
メインのマージソート関数
function mergeSort(arr) {
// Base case
if (arr.length <= 1) {
return arr;
}
// Divide
const middle = Math.floor(arr.length / 2);
const left = arr.slice(0, middle);
const right = arr.slice(middle);
// Conquer and Combine
return merge(mergeSort(left), mergeSort(right));
}
マージソートの内訳:
- 基本ケース:
if (arr.length <= 1) {
return arr;
}
- 長さ 0 または 1 の配列を処理します
- これらはすでに定義に従って並べ替えられています
- 再帰の停止点として機能します
- 分裂フェーズ:
const middle = Math.floor(arr.length / 2); const left = arr.slice(0, middle); const right = arr.slice(middle);
- 配列を 2 つの半分に分割します
- lice() は元の を変更せずに新しい配列を作成します
- トランプを半分に切るようなもの
- 再帰的な並べ替えと結合:
return merge(mergeSort(left), mergeSort(right));
- 各半分を再帰的にソートします
- マージ関数を使用してソートされた半分を結合します
- カードを組み合わせる前に、小さなカードの山を分類するようなもの
チュートリアルの例
[38、27、43、3] がどのようにソートされるかを見てみましょう:
- 最初の分割:
// The Merge Helper Function
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// Add remaining elements
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
while (rightIndex < right.length) {
result.push(right[rightIndex]);
rightIndex++;
}
return result;
}
- 2 番目の分割:
const result = []; let leftIndex = 0; let rightIndex = 0;
- マージバック:
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
結論
マージ ソートは、大規模なデータセットで一貫して優れたパフォーマンスを発揮する、非常に効率的な並べ替えアルゴリズムとして際立っています。単純な並べ替えアルゴリズムと比較して追加のスペースが必要ですが、その O(n log n) 時間の複雑さにより、パフォーマンスが重要な多くの実世界のアプリケーションにとって頼りになる選択肢となります。
重要なポイント:
- 分割統治戦略を使用します
- すべてのケースで O(n log n) 時間計算量
- O(n) 個の追加スペースが必要です
- 安定した並べ替えアルゴリズム
- 大規模なデータセットに最適
常に最新情報を入手してつながりを保つ
このシリーズのどの部分も見逃さないようにし、さらに詳しく知りたい場合は私と連絡を取ってください
ソフトウェア開発 (Web、サーバー、モバイル、またはスクレイピング / オートメーション)、データに関するディスカッション
構造やアルゴリズム、その他のエキサイティングな技術トピックについては、フォローしてください:

エマニュエル・アインデ
- GitHub
- リンクトイン
- X (Twitter)
コーディングを楽しみにしていてください???
以上がマージソートアルゴリズムを理解する: ソートアルゴリズムをマスターするための初心者向けガイドの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

