ホームページ > 記事 > バックエンド開発 > numpy&#s einsum の理不尽な有用性

numpy&#s einsum の理不尽な有用性

Patricia Arquetteオリジナル: 2024-11-04 07:15:02132ブラウズ

導入

Python で最も便利なメソッド、np.einsum を紹介します。 np.einsum (および Tensorflow と JAX の対応するもの) を使用すると、複雑な行列とテンソルの演算を非常に明確かつ簡潔な方法で作成できます。また、その明快さと簡潔さにより、テンソルの操作に伴う精神的な過負荷の多くが軽減されることもわかりました。実際、学習と使用は非常に簡単です。仕組みは次のとおりです: np.einsum には添字文字列引数があり、1 つ以上のオペランドがあります。

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

添字引数は、オペランドの軸を操作および結合する方法を numpy に指示する「ミニ言語」です。最初は少し読みにくいですが、コツを掴めば悪くありません。

単一オペランド

最初の例として、np.einsum を使用して行列 A: の軸を交換してみましょう (別名転置)。

M = np.einsum('ij->ji', A)

文字 i と j は、A の 1 番目と 2 番目の軸にバインドされます。Numpy は、出現する順序で文字を軸にバインドしますが、明示的であれば、numpy は使用する文字を気にしません。たとえば、a と b を使用することもできますが、同じように機能します。

M = np.einsum('ab->ba', A)

ただし、オペランド内の軸と同じ数の文字を指定する必要があります。 A には 2 つの軸があるため、2 つの異なる文字を指定する必要があります。次の例は、機能しません。下付き文字式にはバインドする文字が 1 文字しかないためです。i:

# broken
M = np.einsum('i->i', A)

一方、オペランドの軸が実際に 1 つだけの場合 (つまり、ベクトルです)、1 文字の添え字式は問題なく機能しますが、ベクトルをそのままにするためあまり役に立ちません。現状のまま:

m = np.einsum('i->i', a)

軸上の合計

しかし、この作戦はどうでしょうか? 右側にはiがありません。これは有効ですか?

c = np.einsum('i->', a)

驚いたことに、そうです! np.einsum の本質を理解するための最初の鍵は次のとおりです。軸が右側から省略されている場合、軸は合計されます。 The Unreasonable Usefulness of numpy

コード:

c = 0
I = len(a)
for i in range(I):
   c += a[i]

合計の動作は単一の軸に限定されません。たとえば、次の添字式を使用すると、2 つの軸を一度に合計できます: c = np.einsum('ij->', A): The Unreasonable Usefulness of numpy

両方の軸に対応する Python コードを次に示します。

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

しかし、それだけではありません。創造力を発揮していくつかの軸を合計し、他の軸はそのままにすることもできます。例: np.einsum('ij->i', A) は行列 A の行を合計し、長さ j の行合計のベクトルを残します: The Unreasonable Usefulness of numpy

コード:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

同様に、np.einsum('ij->j', A) は A の列を合計します。 The Unreasonable Usefulness of numpy

コード:

M = np.einsum('ij->ji', A)

2 つのオペランド

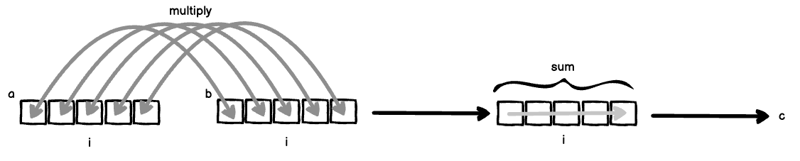
単一のオペランドで実行できることには制限があります。 2 つのオペランドを使用すると、物事はさらに面白く (そして便利に) なります。 2 つのベクトル a = [a_1, a_2, ... ] と b = [a_1, a_2, ...] があると仮定します。 len(a) === len(b) の場合、次のように内積 (ドット積とも呼ばれます) を計算できます。

M = np.einsum('ab->ba', A)

ここでは 2 つのことが同時に起こっています:

i は a と b の両方にバインドされているため、a と b は「並んで」から乗算されます: a[i] * b[i]。
右辺からインデックス i が除外されているため、それを除くために軸 i を合計します。

(1) と (2) を組み合わせると、古典的な内積が得られます。 The Unreasonable Usefulness of numpy

コード:

# broken
M = np.einsum('i->i', A)

さて、添え字の式から i を省略しなかったと仮定しましょう。すべての a[i] と b[i] を乗算し、i の合計をしませんします。

m = np.einsum('i->i', a)

コード:

c = np.einsum('i->', a)

これは要素ごとの乗算 (または行列のアダマール積) とも呼ばれ、通常は numpy メソッド np.multiply を介して実行されます。添字の公式には、外積と呼ばれる 3 番目のバリエーションがまだあります。

c = 0
I = len(a)
for i in range(I):
   c += a[i]

この添字式では、a と b の軸は別々の文字にバインドされているため、別々の「ループ変数」として扱われます。したがって、C には、すべての i と j に対して行列に配置されたエントリ a[i] * b[j] があります。 The Unreasonable Usefulness of numpy

コード:

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

3 つのオペランド

外積をさらに一歩進めて、3 オペランドのバージョンを次に示します。

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

3 つのオペランドの外積に相当する Python コードは次のとおりです。

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

さらに進むと、軸の右側に ik の代わりに ki を書くことで結果を転置するだけでなく、軸を省略して合計することを妨げるものは何もありません。 ->:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

同等の Python コードは次のようになります:

M = np.einsum('ij->ji', A)

これで、複雑なテンソル演算を簡単に指定する方法がわかっていただけたと思います。 numpy をより広範囲に使用したとき、複雑な tensor 演算を実装する必要があるときは必ず np.einsum に手を伸ばすようになりました。私の経験では、np.einsum を使用すると、後でコードを読みやすくなります。上記の演算を添え字から直接読み取ることができます。「3 つのベクトルの外積、中間軸の合計、および最終結果の転置」」。複雑な一連の厄介な操作を読まなければならなかった場合、私は舌を巻くかもしれません。

実用的な例

実際的な例として、古典的な論文「Attending is All You Need」から、LLM の中心となる方程式を実装してみましょう。式1 では、注意メカニズムについて説明します: The Unreasonable Usefulness of numpy

用語に焦点を当てます。

Q K^{T} QK^T

なぜなら、softmax は np.einsum とスケーリング係数では計算できないからです。

\frac{1}{\sqrt{d_{k}}} フラク{1}{sqrt{d_k}}

適用するのは簡単です。

$Q K^{T} QK^T$ term は、n 個のキーを使用した m 個のクエリのドット積を表します。 Q は行列に積み上げられた m 個の d 次元行ベクトルのコレクションであるため、Q の形状は md です。同様に、K は行列に積み上げられた n 個の d 次元行ベクトルのコレクションであるため、K の形状は md になります。

単一の Q と K の間の積は次のように記述されます:

np.einsum('md,nd->mn', Q, K)

添字方程式の記述方法により、行列の乗算の前に K を転置する必要がなくなったことに注意してください。

The Unreasonable Usefulness of numpy

これは非常に簡単そうに見えますが、実際には、単なる伝統的な行列の乗算にすぎません。しかし、まだ終わっていません。 Attending Is All You Need は マルチヘッドアテンション を使用します。これは、Q 行列と K 行列のインデックス付きコレクションに対して、実際に k 個の行列乗算が同時に発生することを意味します。 .

物事をもう少し明確にするために、製品を次のように書き換えることができます。 $Q_{i} K_{i}^{T} Q_iK_i^T$ .

つまり、Q と K の両方に追加の軸 i があることを意味します。

さらに、私たちがトレーニング環境にいる場合、おそらくそのような多頭の注意操作のバッチを実行していることになります。

おそらく、バッチ軸 b に沿ってサンプルのバッチに対して操作を実行したいと考えられます。したがって、完成した製品は次のようになります:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

ここでは 4 軸テンソルを扱っているため、図を省略します。しかし、前の図を「スタッキング」してマルチヘッド軸 i を取得し、次にそれらの「スタック」を「スタッキング」してバッチ軸 b を取得することをイメージできるかもしれません。

他の numpy メソッドを組み合わせてこのような操作をどのように実装するかを理解するのは困難です。しかし、少し調べてみれば、何が起こっているかは明らかです。バッチ全体、行列 Q と K のコレクションに対して、行列乗算 Qt(K) を実行します。

さて、それは素晴らしいことではありませんか?

恥知らずなプラグ

創設者モードのグラインドを 1 年間行った後、仕事を探しています。私はさまざまな技術分野とプログラミング言語で 15 年以上の経験があり、チームの管理も経験しました。数学と統計が重点分野です。 DMして話しましょう!

以上がnumpy&#s einsum の理不尽な有用性の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

Python qt batch numpy String if for math using Length Collection len this tensorflow

声明：

この記事の内容はネチズンが自主的に寄稿したものであり、著作権は原著者に帰属します。このサイトは、それに相当する法的責任を負いません。盗作または侵害の疑いのあるコンテンツを見つけた場合は、admin@php.cn までご連絡ください。

前の記事：Pandas の集計結果で科学表記を抑制するにはどうすればよいですか?次の記事：Pandas の集計結果で科学表記を抑制するにはどうすればよいですか?

続きを見る