回帰アルゴリズムのメトリクス

回帰アルゴリズムのエラーメトリクス

回帰アルゴリズムを作成し、このモデルがどの程度効率的であったかを知りたい場合、エラー メトリクスを使用して機械学習モデルのエラーを表す値を取得します。この記事のメトリクスは、数値 (実数、整数) の予測モデルの誤差を測定する場合に重要です。

この記事では、Python で手動で計算を実行し、ドル相場データセットで機械学習モデルの誤差を測定する、回帰アルゴリズムの主な誤差メトリクスについて説明します。

対処する指標

• SE — 誤差の合計
• 私 — 平均誤差
• MAE — 平均絶対誤差
• MPE — 平均誤差パーセンテージ
• MAPAE — 平均絶対パーセント誤差

両方のメトリクスは少し似ています。ここでは、エラーの平均とパーセンテージのメトリクスと、エラーの平均と絶対パーセンテージのメトリクスがあり、一方のグループが差の実際の値を取得し、もう一方のグループが絶対値を取得するように区別されています。違いの。どちらの指標でも、値が低いほど予測が適切であることを覚えておくことが重要です。

SE — 誤差の合計

SE メトリックは、この記事の中で最も単純なもので、その式は次のとおりです。

SE = εR — P

したがって、実際の値 (モデルの目的変数) と予測値の差の合計になります。このメトリクスには、値を絶対値として扱わないなど、いくつかのマイナス点があり、その結果、偽の値が発生します。

ME — 誤差の平均値

ME メトリクスは SE の「補完」ですが、基本的には要素数を考慮して SE の平均を取得するという違いがあります。

ME = ε(R-P)/N

SE とは異なり、SE の結果を要素の数で割るだけです。この指標は SE と同様に規模に依存します。つまり、同じデータセットを使用する必要があり、異なる予測モデルと比較できます。

MAE — 平均絶対誤差

MAE メトリックは ME ですが、絶対 (負ではない) 値のみを考慮します。実際と予測の差を計算すると、負の結果が得られる場合があり、この負の差は以前のメトリクスに適用されます。このメトリックでは、差を正の値に変換し、要素の数に基づいて平均を取る必要があります。

MPE — 平均パーセンテージ誤差

MPE メトリックは、各差の合計に対するパーセンテージとしての平均誤差です。ここでは、差のパーセンテージを取得し、それを加算し、それを要素の数で割って平均を取得する必要があります。したがって、実際の値と予測値の差が求められ、実際の値で割って 100 を掛け、このパーセンテージをすべて合計して要素の数で割ります。この指標はスケール (%) とは独立しています。

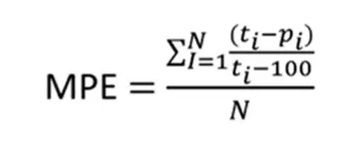
MAPAE — 平均絶対パーセント誤差

MAPAE メトリクスは前のメトリクスとよく似ていますが、予測値と実際値の差は絶対的に作成されます。つまり、正の値を使用して計算されます。したがって、このメトリクスはエラーのパーセンテージの絶対差です。この指標もスケールに依存しません。

実際にメトリクスを使用する

各メトリックの説明を踏まえて、ドル為替レート機械学習モデルからの予測に基づいて Python で両方を手動で計算します。現在、ほとんどの回帰メトリクスは Sklearn パッケージの既製の関数に存在しますが、ここでは教育目的のみを目的として手動で計算します。

RandomForest アルゴリズムとデシジョン ツリー アルゴリズムは、2 つのモデル間の結果を比較するためにのみ使用します。

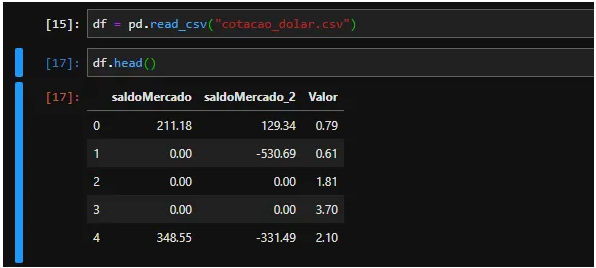
データ分析

私たちのデータセットには、Value 列 (ドル相場) に影響を与える情報である SaldoMercado と saldoMercado_2 の列があります。ご覧のとおり、MercadoMercado 残高は Merado_2 残高よりも見積と密接な関係があります。また、欠損値 (無限値または Nan 値) がなく、balanceMercado_2 列に多くの非絶対値があることを観察することもできます。

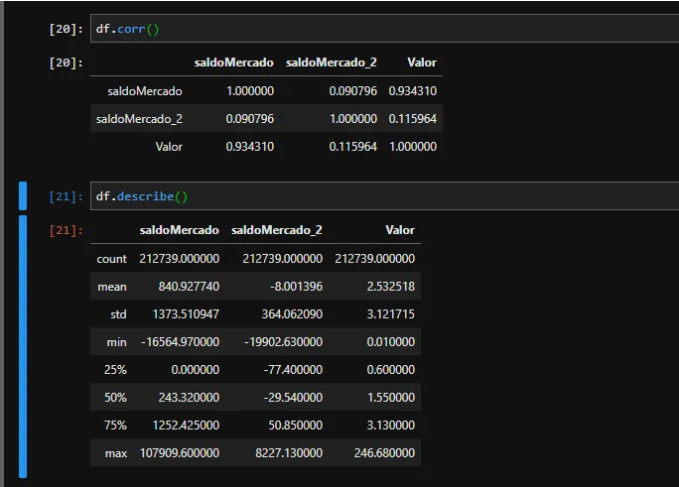
モデルの準備

予測変数と予測する変数を定義することにより、機械学習モデルの値を準備します。 train_test_split を使用して、データをテスト用に 30%、トレーニング用に 70% にランダムに分割します。

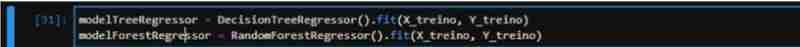
最後に、両方のアルゴリズム (RandomForest と DecisionTree) を初期化し、データを適合させ、テスト データを使用して両方のスコアを測定します。 TreeRegressor では 83%、ForestRegressor では 90% のスコアが得られました。理論的には、ForestRegressor のパフォーマンスが優れていることを示しています。

結果と分析

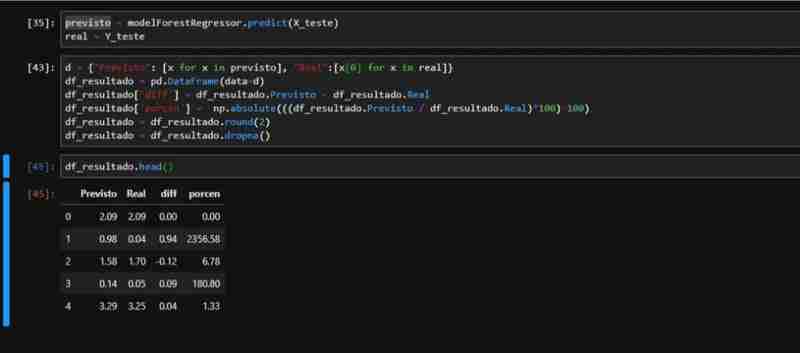
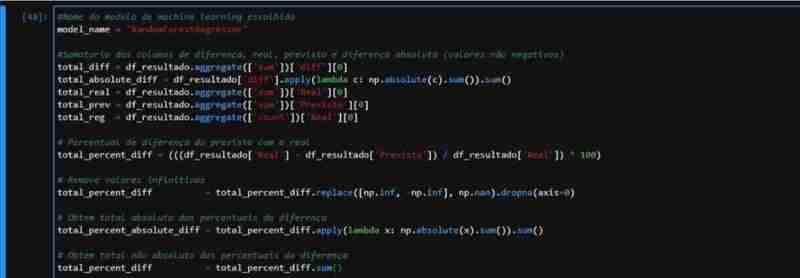
ForestRegressor の部分的に観察されたパフォーマンスを考慮して、メトリクスを適用するために必要なデータを含むデータセットを作成しました。テスト データに対して予測を実行し、差分とパーセンテージの列を含む実際の値と予測値を含む DataFrame を作成します。

ドルレートとモデルが予測したレートの実際の合計との関係で次のことがわかります。

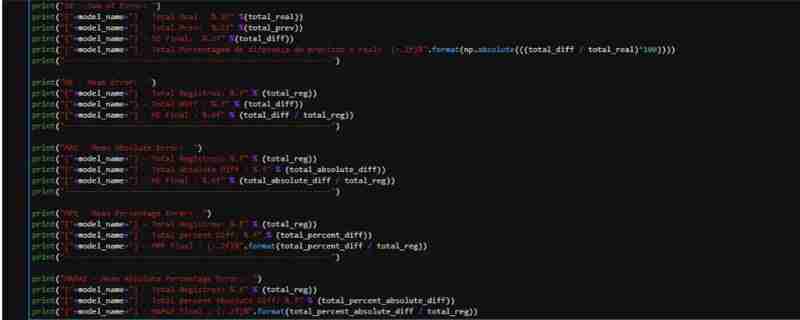
• 合計 R$578.00 の差額がありました
• これは、予測値と実際の値の間の 0.36% の差を表します (絶対値は考慮されません)
• 平均誤差 (ME) に関しては、平均 R$0.009058 という低い値でした
• 絶対平均の場合、データセットに負の値があるため、この値は少し増加します

ここでは教育目的で計算を手動で実行していることを強調します。ただし、パフォーマンスが向上し、計算エラーが発生する可能性が低いため、Sklearn パッケージのメトリクス関数を使用することをお勧めします。

完全なコードは私の GitHub で入手できます: github.com/AirtonLira/artigo_metricasregressao

---

著者: エアトン・リラ・ジュニア

LinkedIn: linkedin.com/in/airton-lira-junior-6b81a661/

以上が回帰アルゴリズムのメトリクスの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。