リンクされたリストに最大公約数を挿入する

2807。リンクされたリストに最大公約数を挿入

難易度: 中

トピック: 連結リスト、数学、数論

各ノードに整数値が含まれるリンク リストの先頭の先頭を指定します。

隣接するノードの各ペアの間に、それらの最大公約数に等しい値を持つ新しいノードを挿入します。

挿入後のリンクされたリストを返します。

2 つの数値の 最大公約数 は、両方の数値を均等に割る最大の正の整数です。

例 1:

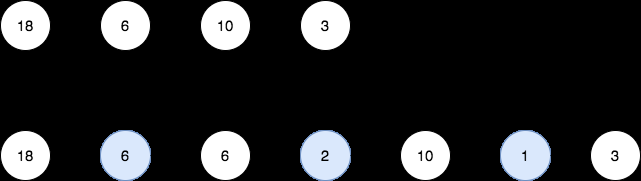
• 入力: head = [18,6,10,3]
• 出力: [18,6,6,2,10,1,3]
• 説明: 1^番目の図は最初のリンク リストを示し、2^番目の図は新しいノードを挿入した後のリンク リストを示します (青色のノードは挿入されたノードです)ノード)。
  • 1^番目と 2^番目ノードの間に、18 と 6 = 6 の最大公約数を挿入します。
  • 2^番目と 3^番目ノードの間に、6 と 10 = 2 の最大公約数を挿入します。
  • 3 番目の ^{ノードと 4 番目の} ノードの間に 10 と 3 = 1 の最大公約数を挿入します。 隣接するノードはもうないので、リンクされたリストを返します。

例 2:

入力:
• head = [7]
出力:
• [7]
説明:
• 1st図は最初のリンク リストを示し、2^nd図は新しいノードを挿入した後のリンク リストを示します。 隣接するノードのペアがないため、最初のリンク リストを返します。

例 3:

入力:
• コスト = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
出力:
• 10

制約:

リスト内のノード数は [1, 5000] の範囲内です。

• 1

ヒント:

左側の各ポイントは、左側のノードに既に接続されているポイントに正確に接続されるか、どのノードにも接続されていない右側のノードのサブセットに接続されます。

1. ビットマスクを使用した動的プログラミングを使用します。状態は (最初のグループに割り当てられたポイントの数、2 番目のグループに割り当てられたポイントのビットマスク) になります。

解決策:

リンクされたリスト内の隣接するノードのすべてのペアの間にノードを挿入する必要があります。挿入されたノードの値は、2 つの隣接するノードの値の最大公約数 (GCD) である必要があります。リンクされたリストを走査し、隣接するノードのすべてのペアの GCD を計算し、それに応じて新しいノードを挿入します。

これに対処する方法は次のとおりです:

ListNode クラスを定義します
1. : このクラスは、リンクされたリスト内の各ノードを表します。
リストを走査
2. : リストを反復処理して、隣接するノードの各ペアを見つけます。
GCD ノードの挿入
3. : 隣接するノードのペアごとに、値が 2 つの隣接するノードの GCD である新しいノードを挿入します。
変更されたリストを返します
4. .
このソリューションを PHP で実装してみましょう:

2807。リンクされたリストに最大公約数を挿入

説明：

<?php
// Definition for a singly-linked list node.
class ListNode {
    public $val = 0;
    public $next = null;

    public function __construct($val = 0, $next = null) {
        $this->val = $val;
        $this->next = $next;
    }
}

/**
 * Function to calculate the GCD of two numbers.
 *
 * @param $a
 * @param $b
 * @return mixed
 */
function gcd($a, $b) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */

}

/**
 * @param ListNode $head
 * @return ListNode
 */
function insertGreatestCommonDivisors($head) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Function to print the linked list for testing purposes.
 * 
 * @param $head
 * @return void
 */
function printList($head) {
    $current = $head;
    while ($current != null) {
        echo $current->val . " ";
        $current = $current->next;
    }
    echo "\n";
}

// Example usage:

// Create the linked list: 18 -> 6 -> 10 -> 3
$head = new ListNode(18);
$head->next = new ListNode(6);
$head->next->next = new ListNode(10);
$head->next->next->next = new ListNode(3);

// Insert GCD nodes.
$modifiedHead = insertGreatestCommonDivisors($head);

// Print the modified linked list.
printList($modifiedHead);

// Output should be: 18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3
?>

1. ListNode クラス

   : このクラスは、値 ($val) と次のノード ($next) のプロパティを備えたリンク リスト内のノードの構造を表します。

2. GCD 計算

   : gcd 関数は、ユークリッド アルゴリズムを使用して 2 つの整数の最大公約数を計算します。

3. メインロジック (GreatestCommonDivisors を挿入)

   :

   最後から 2 番目のノードに到達するまで、リンク リストをループします。
   • 隣接するノードのペアごとに、それらの値の GCD を計算します。
   • この GCD 値を使用して新しいノードを作成し、現在のノードと次のノードの間に挿入します。
4. エッジケース

   : リストにノードが 1 つだけある場合は、隣接するノードがないため、変更を加えずにそのまま返します。

5. テスト

   : 関数 printList は、検証のためにリンク リストの値を出力するために使用されるヘルパー関数です。

Time Complexity:

• The time complexity of this solution is (O(n)), where (n) is the number of nodes in the linked list. Calculating the GCD for each adjacent pair takes constant time on average, and we perform a linear traversal of the list.

Example:

For the input list [18, 6, 10, 3], the output is:

18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub

以上がリンクされたリストに最大公約数を挿入するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。