最短経路の検索

2 つの頂点間の最短パスは、合計重みが最小のパスです。
エッジに非負の重みを持つグラフを与えて、2 つの頂点間の最短経路を見つけるためのよく知られたアルゴリズムは、オランダのコンピューター科学者である Edsger Dijkstra によって発見されました。頂点 s から頂点 v までの最短経路を見つけるために、ダイクストラのアルゴリズム は s からすべての頂点までの最短経路を見つけます。したがって、ダイクストラのアルゴリズムは、単一ソースの最短経路アルゴリズムとして知られています。このアルゴリズムは、cost[v]を使用して、頂点vからソース頂点sまでの最短パスのコストを保存します。 コスト[s]は0です。最初に、他のすべての頂点の cost[v] に無限大を割り当てます。このアルゴリズムは、V – T で最小の コスト[u] を持つ頂点 u を繰り返し見つけ、u を T に移動します。 .

アルゴリズムは以下のコードで説明されています。

Input: a graph G = (V, E) with non-negative weights
Output: a shortest path tree with the source vertex s as the root
 1 ShortestPathTree getShortestPath(s) {
 2 Let T be a set that contains the vertices whose
 3 paths to s are known; Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T  cost[u] + w(u, v)) {
11 cost[v] = cost[u] + w(u, v); parent[v] = u;
12 }
13 }
14 }

このアルゴリズムは、最小スパニング ツリーを見つけるための Prim のアルゴリズムに非常に似ています。どちらのアルゴリズムも、頂点を T と V - T の 2 つのセットに分割します。 Prim のアルゴリズムの場合、set T には、すでにツリーに追加されている頂点が含まれます。ダイクストラの場合、セット T には、ソースへの最短パスが見つかった頂点が含まれます。どちらのアルゴリズムも、V – T から頂点を繰り返し見つけて、それを T に追加します。プリムのアルゴリズムの場合、頂点は、エッジの重みが最小であるセット内のいくつかの頂点に隣接します。ダイクストラのアルゴリズムでは、頂点はソースへの総コストが最小となるセット内のいくつかの頂点に隣接します。

アルゴリズムは、cost[s] を 0 に設定することから始まり (4 行目)、他のすべての頂点の cost[v] を無限大に設定します。次に、最小の コスト[u]で V – T から T に頂点 (u とします) を継続的に追加します (7 行目 – 8)、以下の図に示すように。 u を T に追加した後、アルゴリズムは各 vcost[v] と parent[v] を更新します。 > (u, v) が T かつ cost[v] > にある場合、T にはありません。 cost[u] + w(u, v) (10 ～ 11 行目).

下の図 a のグラフを使用して、ダイクストラのアルゴリズムを説明しましょう。ソース頂点が

1 であるとします。したがって、cost[1] = 0 であり、下の図 b に示すように、他のすべての頂点のコストは最初は ∞ です。 parent[i] を使用して、パス内の i の親を示します。便宜上、ソース ノードの親を -1 に設定します。

初期設定の

Tは空です。アルゴリズムはコストが最小の頂点を選択します。この場合、頂点は 1 です。以下の図に示すように、アルゴリズムは 1 を T に加算します。その後、1 に隣接する各頂点のコストを調整します。以下の図 b に示すように、頂点 2、0、6、3 とその親のコストが更新されます。

頂点

2、0、6、および 3 はソース頂点に隣接しており、頂点 2 は V-T 内のコストが最小のものであるため、以下の図に示すように 2 を T に追加し、頂点のコストと親を更新します。 V-T であり、2 に隣接しています。 cost[0] は 6 に更新され、その親は 2 に設定されます。 1 から 2 への矢印線は、2 が 2 に追加された後、1 が 2 の親であることを示します。 た

.

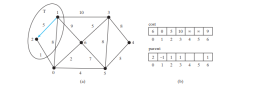
現在、T には {1、2} が含まれています。頂点 0 はコストが最小の V-T の頂点であるため、以下の図に示すように 0 を T に追加し、 V-T 内で、該当する場合は 0 に隣接する頂点のコストと親。 cost[5] は 10 に更新され、その親は 0 に設定され、cost[6] は 8 であり、その親は 0 に設定されています。

現在、

T には {1、2、0} が含まれています。頂点 6 はコストが最小の V-T の頂点であるため、以下の図に示すように 6 を T に追加し、該当する場合、V-T および 6 に隣接する頂点のコストと親。

現在、

T には {1、2、0、6} が含まれています。頂点 3 または 5 は、V-T 内でコストが最も小さい頂点です。 3 または 5 を T に追加できます。以下の図に示すように、3 を T に追加し、V-T 内で 3 に隣接する頂点のコストと親を更新しましょう。該当する場合。 cost[4] は 18 に更新され、その親は 3 に設定されます。

現在、

T には、{1、2、0、6、3}。頂点 5 はコストが最小の V-T の頂点であるため、以下の図に示すように 5 を T に追加し、 V-T 内にあり、該当する場合は 5 に隣接する頂点のコストと親。 cost[4] は 10 に更新され、その親は 5 に設定されます。

現在、

T

には、{1、2、0、6、3、5}。 V-T 内の頂点 4 はコストが最小の頂点であるため、下の図に示すように 4 を T に追加します。

ご覧のとおり、アルゴリズムは基本的にソース頂点からのすべての最短パスを検索し、ソース頂点をルートとするツリーを生成します。このツリーを 単一ソースの全最短パス ツリー

(または単に

最短パス ツリー) と呼びます。このツリーをモデル化するには、以下の図に示すように、Tree クラスを拡張する ShortestPathTree という名前のクラスを定義します。 ShortestPathTree は、WeightedGraph.java. の行 200 ～ 224 で WeightedGraph の内部クラスとして定義されています。

getShortestPath(int sourceVertex)

メソッドは、WeightedGraph.java の 156 ～ 197 行目に実装されました。このメソッドは、

cost[sourceVertex] を 0 に設定し (162 行目)、他のすべての頂点の cost[v] を無限大に設定します (159 ～ 161 行目)。 sourceVertex の親は -1 に設定されます (166 行目)。 T は、最短パス ツリーに追加された頂点を格納するリストです (169 行目)。 T に追加された頂点の順序を記録するために、セットではなく T のリストを使用します。 最初、T

は空です。

T を展開するには、メソッドは次の操作を実行します。

1. Find the vertex u with the smallest cost[u] (lines 175–181) and add it into T (line 183).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > cost[u] + w(u, v) (lines 186–192).

Once all vertices from s are added to T, an instance of ShortestPathTree is created (line 196).

The ShortestPathTree class extends the Tree class (line 200). To create an instance of ShortestPathTree, pass sourceVertex, parent, T, and cost (lines 204–205). sourceVertex becomes the root in the tree. The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n^3).

Dijkstra’s algorithm is a combination of a greedy algorithm and dynamic programming. It is a greedy algorithm in the sense that it always adds a new vertex that has the shortest distance to the source. It stores the shortest distance of each known vertex to the source and uses it later to avoid redundant computing, so Dijkstra’s algorithm also uses dynamic programming.

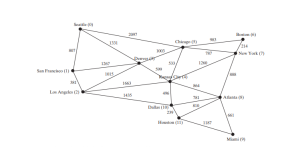
The code below gives a test program that displays the shortest paths from Chicago to all other cities in Figure below and the shortest paths from vertex 3 to all vertices for the graph in Figure below a, respectively.

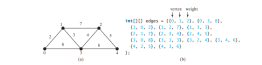
package demo;

public class TestShortestPath {

    public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<string> graph1 = new WeightedGraph(vertices, edges);
        WeightedGraph<string>.ShortestPathTree tree1 = graph1.getShortestPath(graph1.getIndex("Chicago"));
        tree1.printAllPaths();

        // Display shortest paths from Houston to Chicago       
        System.out.println("Shortest path from Houston to Chicago: ");
        java.util.List<string> path = tree1.getPath(graph1.getIndex("Houston"));
        for(String s: path) {
            System.out.print(s + " ");
        }

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<integer> graph2 = new WeightedGraph(edges, 5);
        WeightedGraph<integer>.ShortestPathTree tree2 = graph2.getShortestPath(3);
        System.out.println("\n");
        tree2.printAllPaths();
    }

}

</integer></integer></string></string></string>

All shortest paths from Chicago are:
A path from Chicago to Seattle: Chicago Seattle (cost: 2097.0)
A path from Chicago to San Francisco:
Chicago Denver San Francisco (cost: 2270.0)
A path from Chicago to Los Angeles:
Chicago Denver Los Angeles (cost: 2018.0)
A path from Chicago to Denver: Chicago Denver (cost: 1003.0)
A path from Chicago to Kansas City: Chicago Kansas City (cost: 533.0)
A path from Chicago to Chicago: Chicago (cost: 0.0)
A path from Chicago to Boston: Chicago Boston (cost: 983.0)
A path from Chicago to New York: Chicago New York (cost: 787.0)
A path from Chicago to Atlanta:
Chicago Kansas City Atlanta (cost: 1397.0)
A path from Chicago to Miami:
Chicago Kansas City Atlanta Miami (cost: 2058.0)
A path from Chicago to Dallas: Chicago Kansas City Dallas (cost: 1029.0)
A path from Chicago to Houston:
Chicago Kansas City Dallas Houston (cost: 1268.0)
Shortest path from Houston to Chicago:
Houston Dallas Kansas City Chicago

All shortest paths from 3 are:
A path from 3 to 0: 3 1 0 (cost: 5.0)
A path from 3 to 1: 3 1 (cost: 3.0)
A path from 3 to 2: 3 2 (cost: 4.0)
A path from 3 to 3: 3 (cost: 0.0)
A path from 3 to 4: 3 4 (cost: 6.0)

The program creates a weighted graph for Figure above in line 27. It then invokes the getShortestPath(graph1.getIndex("Chicago")) method to return a Path object that contains all shortest paths from Chicago. Invoking printAllPaths() on the ShortestPathTree object displays all the paths (line 30).

The graphical illustration of all shortest paths from Chicago is shown in Figure below. The shortest paths from Chicago to the cities are found in this order: Kansas City, New York, Boston, Denver, Dallas, Houston, Atlanta, Los Angeles, Miami, Seattle, and San Francisco.

以上が最短経路の検索の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。