データ構造とアルゴリズム: グラフ

導入

グラフは、多数の頂点 (ノード) とそれらの間のエッジ (接続) を持つデータ構造です。

ツリーはグラフの一例です。すべてのツリーはグラフですが、すべてのグラフがツリーであるわけではありません。たとえば、サイクルを持つグラフはツリーではありません。ツリーには 2 つのノード間に 1 つのルートと 1 つの固有のパスがありますが、グラフには頂点間に多数のルートと複数のパスがある可能性があります。

基本用語

頂点: グラフ内のノード。

エッジ: 2 つの頂点間の接続。

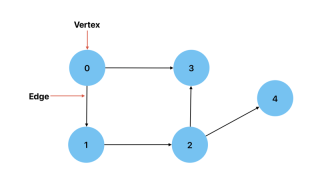
Directed: 2 つの頂点間の接続に方向がある場合。これは、ある頂点から別の頂点に到達する方法が 1 つしかないことを意味します。例としては、都市 (頂点) とそれらの間のルート (エッジ) を示すグラフが考えられます。

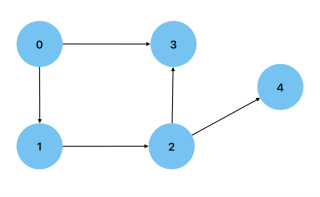
無向: グラフ上の 2 つの頂点間の接続が双方向になる場合。例としては、友情によってつながっている人々 (頂点) を示すグラフが考えられます。

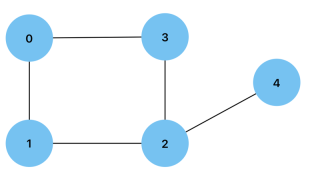
Degree: 頂点に接続されているエッジの数。有向グラフの頂点は、それぞれ頂点に向かうエッジと頂点から遠ざかるエッジの数である入次数または出次数を持つことができます。

Weighted: エッジに重みとして値を持つグラフ。例としては、ノード間の距離が重みとして表される道路マップが挙げられます。

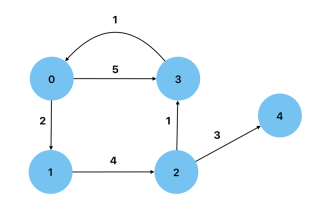
Cyclic: 少なくとも 1 つの頂点からそれ自体に戻るパスを持つグラフ。

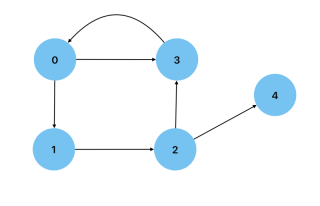
Acyclic: サイクルを持たないグラフ。つまり、ノード自体に戻るパスを持たないグラフ。 有向非巡回グラフ は、データ処理フローを示すために使用できるグラフの一種です。

密: グラフのエッジが最大数に近い場合

Sparse: グラフのエッジが最小数に近い場合。

自己ループ: エッジにそれ自体にリンクする頂点が 1 つある場合。

マルチエッジ: グラフの 2 つの頂点間に複数のエッジがある場合。

単純: グラフに自己ループもマルチエッジもない場合。

単純な有向グラフのエッジの最大数を取得するには: n*(n-1) ここで、n はノードの数です。

単純な無向グラフのエッジの最大数を取得するには: n*(n-1)/2 ここで、n はノードの数です。

JavaScript でのグラフの実装

グラフを実装するには、グラフの頂点とエッジを指定することから始めることができます。以下は、次のグラフを例にしてこれを行う方法の例です:

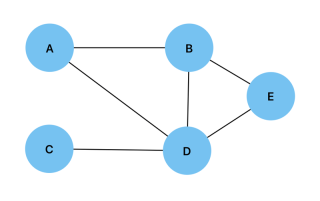
const vertices = ["A", "B", "C", "D", "E"];

const edges = [
  ["A", "B"],
  ["A", "D"],
  ["B", "D"],
  ["B", "E"],
  ["C", "D"],
  ["D", "E"],
];

次に、指定された頂点に隣接するものを見つける関数を作成できます。

const findAdjacentNodes = function (node) {
  const adjacentNodes = [];
  for (let edge of edges) {
    const nodeIndex = edge.indexOf(node);
    if (nodeIndex > -1) {
      let adjacentNode = nodeIndex === 0 ? edge[1] : edge[0];
      adjacentNodes.push(adjacentNode);
    }
  }
  return adjacentNodes;
};

2 つの頂点が接続されているかどうかを確認する別の関数:

const isConnected = function (node1, node2) {
  const adjacentNodes = new Set(findAdjacentNodes(node1));
  return adjacentNodes.has(node2);
};

隣接リスト

隣接リストは、ノードに接続されているすべての頂点がリストとして保存されているグラフの表現です。以下は、対応する隣接リストのグラフと視覚的表現です。

隣接リストは、Node クラスと Graph クラスの 2 つのクラスを作成することで JavaScript で実装できます。 Node クラスは、コンストラクターと 2 つの頂点を結合する connect() メソッドで構成されます。また、上記とまったく同じように動作する isConnected() メソッドと getAdjacentNodes() メソッドもあります。

class Node {
  constructor(value) {
    this.value = value;
    this.edgesList = [];
  }
  connect(node) {
    this.edgesList.push(node);
    node.edgesList.push(this);
  }
  getAdjNodes() {
    return this.edgesList.map((edge) => edge.value);
  }
  isConnected(node) {
    return this.edgesList.map((edge) => 
    edge.value).indexOf(node.value) > -1;
  }
}

Graph クラスは、コンストラクターと、グラフに新しい頂点を追加する addToGraph() メソッドで構成されます。

class Graph {
  constructor(nodes) {
    this.nodes = [...nodes];
  }
  addToGraph(node) {
    this.nodes.push(node);
  }
}

Adjacency Matrix

A 2-D array where each array represents a vertex and each index represents a possible connection between vertices. An adjacency matrix is filled with 0s and 1s, with 1 representing a connection. The value at adjacencyMatrix[node1][node2] will show whether or not there is a connection between the two specified vertices. Below is is a graph and its visual representation as an adjacency matrix.

To implement this adjacency matrix in JavaScript, we start by creating two classes, the first being the Node class:

class Node {
  constructor(value) {
    this.value = value;
  }
}

We then create the Graph class which will contain the constructor for creating the 2-D array initialized with zeros.

class Graph {
  constructor(nodes) {
    this.nodes = [...nodes];
    this.adjacencyMatrix = Array.from({ length: nodes.length },   
    () => Array(nodes.length).fill(0));
   }
}

We will then add the addNode() method which will be used to add new vertices to the graph.

  addNode(node) {
    this.nodes.push(node);
    this.adjacencyMatrix.forEach((row) => row.push(0));
    this.adjacencyMatrix.push(new Array(this.nodes.length).fill(0));
  }

Next is the connect() method which will add an edge between two vertices.

  connect(node1, node2) {
    const index1 = this.nodes.indexOf(node1);
    const index2 = this.nodes.indexOf(node2);

    if (index1 > -1 && index2 > -1) {
      this.adjacencyMatrix[index1][index2] = 1;
      this.adjacencyMatrix[index2][index1] = 1; 
    }
  }

We will also create the isConnected() method which can be used to check if two vertices are connected.

  isConnected(node1, node2) {
    const index1 = this.nodes.indexOf(node1);
    const index2 = this.nodes.indexOf(node2);

    if (index1 > -1 && index2 > -1) {
      return this.adjacencyMatrix[index1][index2] === 1;
    }
    return false;
  }

Lastly we will add the printAdjacencyMatrix() method to the Graph class.

  printAdjacencyMatrix() {
    console.log(this.adjacencyMatrix);
  }

Breadth First Search

Similar to a Breadth First Search in a tree, the vertices adjacent to the current vertex are visited before visiting any subsequent children. A queue is the data structure of choice when performing a Breadth First Search on a graph.

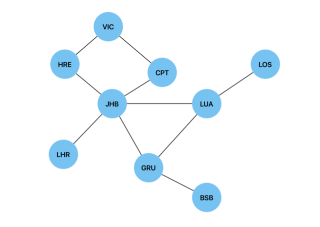
Below is a graph of international airports and their connections and we will use a Breadth First Search to find the shortest route(path) between two airports(vertices).

In order to implement this search algorithm in JavaScript, we will use the same Node and Graph classes we implemented the adjacency list above. We will create a breadthFirstTraversal() method and add it to the Graph class in order to traverse between two given vertices. This method will have the visitedNodes object, which will be used to store the visited vertices and their predecessors. It is initiated as null to show that the first vertex in our search has no predecessors.

breathFirstTraversal(start, end) {
    const queue = [start];
    const visitedNodes = {};
    visitedNodes[start.value] = null;

    while (queue.length > 0) {
      const node = queue.shift();

      if (node.value === end.value) {
        return this.reconstructedPath(visitedNodes, end);
      }
      for (const adjacency of node.edgesList) {
        if (!visitedNodes.hasOwnProperty(adjacency.value)) {
          visitedNodes[adjacency.value] = node;
          queue.push(adjacency);
        }
      }
    }
  }

Once the end vertex is found, we will use the reconstructedPath() method in the Graph class in order to return the shortest path between two vertices. Each vertex is added iteratively to the shortestPath array, which in turn must be reversed in order to come up with the correct order for the shortest path.

reconstructedPath(visitedNodes, endNode) {
    let currNode = endNode;

    const shortestPath = [];

    while (currNode !== null) {
      shortestPath.push(currNode.value);
      currNode = visitedNodes[currNode.value];
    }
    return shortestPath.reverse();
  }

In the case of the graph of international airports, breathFirstTraversal(JHB, LOS) will return JHB -> LUA -> LOS as the shortest path. In the case of a weighted graph, we would use Dijkstra's algorithm to find the shortest path.

Depth First Search

Similar to a depth first search in a tree, this algorithm will fully explore every descendant of a vertex, before backtracking to the root. A stack is the data structure of choice for depth first traversals in a graph.

A depth first search can be used to detect a cycle in a graph. We will use the same graph of international airports to illustrate this in JavaScript.

Similar to the Breadth First Search algorithm above, this implementation of a Depth First Search algorithm in JavaScript will use the previously created Node and Graph classes. We will create a helper function called depthFirstTraversal() and add it to the Graph class.

  depthFirstTraversal(start, visitedNodes = {}, parent = null) {
    visitedNodes[start.value] = true;

    for (const adjacency of start.edgesList) {
      if (!visitedNodes[adjacency.value]) {
        if (this.depthFirstTraversal(adjacency, visitedNodes, start)) {
          return true;
        }
      } else if (adjacency !== parent) {
        return true;
      }
    }

    return false;
  }

This will perform the Depth First Traversal of the graph, using the parent parameter to keep track of the previous vertex and prevent the detection of a cycle when revisiting the parent vertex. Visited vertices will be marked as true in the visitedNodes object. This method will then use recursion to visit previously unvisited vertices. If the vertex has already been visited, we check it against the parent parameter. A cycle has been found if the vertex has already been visited and it is not the parent.

We will also create the wrapper function hasCycle() in the Graph class. This function is used to detect a cycle in a disconnected graph. It will initialize the visitedNodes object and loop through all of the vertices in the graph.

hasCycle() {
    const visitedNodes = {};

    for (const node of this.nodes) {
      if (!visitedNodes[node.value]) {
        if (this.depthFirstTraversal(node, visitedNodes)) {
          return true;
        }
      }
    }
    return false;
  }

In the case of the graph of international airports, the code will return true.

Depth First Traversal of a graph is also useful for pathfinding(not necessarily shortest path) and for solving mazes.

Conclusion

A firm understanding of graphs as a data structure and of their associated algorithms is absolutely necessary when furthering one's studies of data structures and algorithms. Although not as beginner friendly as the previous posts in this series, this guide should prove useful to deepen your understanding of data structures and algorithms.

以上がデータ構造とアルゴリズム: グラフの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。