
配列トラバーサルは、すべての開発者が習得すべきデータ構造とアルゴリズム (DSA) の基本概念です。この包括的なガイドでは、基本的なアプローチから始めて、より高度な方法に進んで、JavaScript で配列を走査するためのさまざまなテクニックを検討します。簡単なレベルから上級レベルまでの 20 の例を取り上げ、学習を強化するための LeetCode スタイルの質問も含めます。
目次
- 配列トラバーサルの概要
-
基本的な配列の走査
- 例 1: for ループの使用
- 例 2: while ループの使用
- 例 3: do-while ループの使用
- 例 4: 逆走査
-
最新の JavaScript 配列メソッド
- 例 5: forEach メソッド
- 例 6: マップメソッド
- 例 7: フィルターメソッド
- 例 8:reduce メソッド
-
中級のトラバーステクニック
- 例 9: 2 ポインター手法
- 例 10: スライディング ウィンドウ
- 例 11: Kadane のアルゴリズム
- 例 12: オランダ国旗アルゴリズム
-
高度なトラバーサル技術
- 例 13: 再帰的走査
- 例 14: ソートされた配列の二分探索
- 例 15: ソートされた 2 つの配列をマージする
- 例 16: クイック選択アルゴリズム
-
特殊なトラバーサル
- 例 17: 2D 配列の走査
- 例 18: スパイラル行列トラバーサル
- 例 19: 斜め移動
- 例 20: ジグザグトラバーサル
- パフォーマンスに関する考慮事項
- LeetCode 練習問題
- 結論
1. 配列トラバーサルの概要
配列トラバーサルは、配列内の各要素にアクセスして何らかの操作を実行するプロセスです。これはプログラミングにおける重要なスキルであり、多くのアルゴリズムやデータ操作の基礎を形成します。 JavaScript では、配列はデータを走査して操作するための複数の方法を提供する多用途のデータ構造です。
2. 基本的な配列の走査
配列トラバーサルの基本的な方法から始めましょう。
例 1: for ループの使用
古典的な for ループは、配列を走査する最も一般的な方法の 1 つです。
function sumArray(arr) {
let sum = 0;
for (let i = 0; i
<p><strong>時間計算量</strong>: O(n)、n は配列の長さです。</p>
<p></p>
<h3>
例 2: while ループの使用
</h3>
<p>while ループは、特に終了条件がより複雑な場合、配列の走査にも使用できます。<br>
</p>
<pre class="brush:php;toolbar:false">function findFirstNegative(arr) {
let i = 0;
while (i = 0) {
i++;
}
return i
<p><strong>時間計算量</strong>: 最悪の場合は O(n) ですが、負の数が早期に見つかった場合は小さくなる可能性があります。</p>
<p></p>
<h3>
例 3: do-while ループの使用
</h3>
<p>do-while ループは配列のトラバーサルではあまり一般的ではありませんが、特定のシナリオでは役立つ場合があります。<br>
</p>
<pre class="brush:php;toolbar:false">function printReverseUntilZero(arr) {
let i = arr.length - 1;
do {
console.log(arr[i]);
i--;
} while (i >= 0 && arr[i] !== 0);
}
const numbers = [1, 3, 0, 5, 7];
printReverseUntilZero(numbers); // Output: 7, 5
時間計算量: 最悪の場合は O(n) ですが、早期にゼロに遭遇した場合はそれより少なくなる可能性があります。
例 4: 逆走査
配列を逆順に走査することは、多くのアルゴリズムで一般的な操作です。
function reverseTraversal(arr) {
const result = [];
for (let i = arr.length - 1; i >= 0; i--) {
result.push(arr[i]);
}
return result;
}
const numbers = [1, 2, 3, 4, 5];
console.log(reverseTraversal(numbers)); // Output: [5, 4, 3, 2, 1]
時間計算量: O(n)、n は配列の長さです。
3. 最新の JavaScript 配列メソッド
ES6 以降のバージョンの JavaScript では、トラバーサルと操作を簡素化する強力な配列メソッドが導入されました。
例 5: forEach メソッド
forEach メソッドは、配列要素を反復処理するクリーンな方法を提供します。
function logEvenNumbers(arr) {
arr.forEach(num => {
if (num % 2 === 0) {
console.log(num);
}
});
}
const numbers = [1, 2, 3, 4, 5, 6];
logEvenNumbers(numbers); // Output: 2, 4, 6
時間計算量: O(n)、n は配列の長さです。
例 6: マップメソッド
map メソッドは、すべての要素に対して提供された関数を呼び出した結果を含む新しい配列を作成します。
function doubleNumbers(arr) {
return arr.map(num => num * 2);
}
const numbers = [1, 2, 3, 4, 5];
console.log(doubleNumbers(numbers)); // Output: [2, 4, 6, 8, 10]
時間計算量: O(n)、n は配列の長さです。
例 7: フィルターメソッド
フィルター メソッドは、特定の条件を通過するすべての要素を含む新しい配列を作成します。
function filterPrimes(arr) {
function isPrime(num) {
if (num
<p><strong>時間計算量</strong>: O(n * sqrt(m))、n は配列の長さ、m は配列内の最大の数です。</p>
<p></p>
<h3>
例 8:reduce メソッド
</h3>
<p>reduce メソッドは、配列の各要素にリデューサ関数を適用し、単一の出力値を生成します。<br>
</p>
<pre class="brush:php;toolbar:false">function findMax(arr) {
return arr.reduce((max, current) => Math.max(max, current), arr[0]);
}
const numbers = [3, 7, 2, 9, 1, 5];
console.log(findMax(numbers)); // Output: 9
時間計算量: O(n)、n は配列の長さです。
4. 中級のトラバーステクニック
次に、配列トラバーサルの中級テクニックをいくつか見てみましょう。
例 9: 2 ポインター手法
2 ポインター手法は、配列関連の問題を効率的に解決するためによく使用されます。
function isPalindrome(arr) {
let left = 0;
let right = arr.length - 1;
while (left
<p><strong>Time Complexity</strong>: O(n/2) which simplifies to O(n), where n is the length of the array.</p>
<p></p>
<h3>
Example 10: Sliding window
</h3>
<p>The sliding window technique is useful for solving problems involving subarrays or subsequences.<br>
</p>
<pre class="brush:php;toolbar:false">function maxSubarraySum(arr, k) {
if (k > arr.length) return null;
let maxSum = 0;
let windowSum = 0;
// Calculate sum of first window
for (let i = 0; i
<p><strong>Time Complexity</strong>: O(n), where n is the length of the array.</p>
<p></p>
<h3>
Example 11: Kadane's Algorithm
</h3>
<p>Kadane's algorithm is used to find the maximum subarray sum in a one-dimensional array.<br>
</p>
<pre class="brush:php;toolbar:false">function maxSubarraySum(arr) {
let maxSoFar = arr[0];
let maxEndingHere = arr[0];
for (let i = 1; i
<p><strong>Time Complexity</strong>: O(n), where n is the length of the array.</p>
<p></p>
<h3>
Example 12: Dutch National Flag Algorithm
</h3>
<p>This algorithm is used to sort an array containing three distinct elements.<br>
</p>
<pre class="brush:php;toolbar:false">function dutchFlagSort(arr) {
let low = 0, mid = 0, high = arr.length - 1;
while (mid
<p><strong>Time Complexity</strong>: O(n), where n is the length of the array.</p>
<p></p>
<h2>
5. Advanced Traversal Techniques
</h2>
<p>Let's explore some more advanced techniques for array traversal.</p>
<p></p>
<h3>
Example 13: Recursive traversal
</h3>
<p>Recursive traversal can be powerful for certain types of problems, especially those involving nested structures.<br>
</p>
<pre class="brush:php;toolbar:false">function sumNestedArray(arr) {
let sum = 0;
for (let element of arr) {
if (Array.isArray(element)) {
sum += sumNestedArray(element);
} else {
sum += element;
}
}
return sum;
}
const nestedNumbers = [1, [2, 3], [[4, 5], 6]];
console.log(sumNestedArray(nestedNumbers)); // Output: 21
Time Complexity: O(n), where n is the total number of elements including nested ones.
Example 14: Binary search on sorted array
Binary search is an efficient algorithm for searching a sorted array.
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left
<p><strong>Time Complexity</strong>: O(log n), where n is the length of the array.</p>
<p></p>
<h3>
Example 15: Merge two sorted arrays
</h3>
<p>This technique is often used in merge sort and other algorithms.<br>
</p>
<pre class="brush:php;toolbar:false">function mergeSortedArrays(arr1, arr2) {
const mergedArray = [];
let i = 0, j = 0;
while (i
<p><strong>Time Complexity</strong>: O(n + m), where n and m are the lengths of the input arrays.</p>
<p></p>
<h3>
Example 16: Quick Select Algorithm
</h3>
<p>Quick Select is used to find the kth smallest element in an unsorted array.<br>
</p>
<pre class="brush:php;toolbar:false">function quickSelect(arr, k) {
if (k arr.length) {
return null;
}
function partition(low, high) {
const pivot = arr[high];
let i = low - 1;
for (let j = low; j k - 1) {
return select(low, pivotIndex - 1, k);
} else {
return select(pivotIndex + 1, high, k);
}
}
return select(0, arr.length - 1, k);
}
const numbers = [3, 2, 1, 5, 6, 4];
console.log(quickSelect(numbers, 2)); // Output: 2 (2nd smallest element)
Time Complexity: Average case O(n), worst case O(n^2), where n is the length of the array.
6. Specialized Traversals
Some scenarios require specialized traversal techniques, especially when dealing with multi-dimensional arrays.
Example 17: Traversing a 2D array
Traversing 2D arrays (matrices) is a common operation in many algorithms.
function traverse2DArray(matrix) {
const result = [];
for (let i = 0; i
<p><strong>Time Complexity</strong>: O(m * n), where m is the number of rows and n is the number of columns in the matrix.</p>
<p></p>
<h3>
Example 18: Spiral Matrix Traversal
</h3>
<p>Spiral traversal is a more complex pattern often used in coding interviews and specific algorithms.<br>
</p>
<pre class="brush:php;toolbar:false">function spiralTraversal(matrix) {
const result = [];
if (matrix.length === 0) return result;
let top = 0, bottom = matrix.length - 1;
let left = 0, right = matrix[0].length - 1;
while (top = left; i--) {
result.push(matrix[bottom][i]);
}
bottom--;
}
if (left = top; i--) {
result.push(matrix[i][left]);
}
left++;
}
}
return result;
}
const matrix = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
console.log(spiralTraversal(matrix));
// Output: [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]
Time Complexity: O(m * n), where m is the number of rows and n is the number of columns in the matrix.
Example 19: Diagonal Traversal
Diagonal traversal of a matrix is another interesting pattern.
function diagonalTraversal(matrix) {
const m = matrix.length;
const n = matrix[0].length;
const result = [];
for (let d = 0; d = 0 && j
<p><strong>Time Complexity</strong>: O(m * n), where m is the number of rows and n is the number of columns in the matrix.</p>
<p></p>
<h3>
Example 20: Zigzag Traversal
</h3>
<p>Zigzag traversal is a pattern where we traverse the array in a zigzag manner.<br>
</p>
<pre class="brush:php;toolbar:false">function zigzagTraversal(matrix) {
const m = matrix.length;
const n = matrix[0].length;
const result = [];
let row = 0, col = 0;
let goingDown = true;
for (let i = 0; i
<p><strong>Time Complexity</strong>: O(m * n), where m is the number of rows and n is the number of columns in the matrix.</p>
<p></p>
<h2>
7. Performance Considerations
</h2>
<p>When working with array traversals, it's important to consider performance implications:</p>
<ol>
<li><p><strong>Time Complexity</strong>: Most basic traversals have O(n) time complexity, where n is the number of elements. However, nested loops or recursive calls can increase this to O(n^2) or higher.</p></li>
<li><p><strong>Space Complexity</strong>: Methods like map and filter create new arrays, potentially doubling memory usage. In-place algorithms are more memory-efficient.</p></li>
<li><p><strong>Iterator Methods vs. For Loops</strong>: Modern methods like forEach, map, and filter are generally slower than traditional for loops but offer cleaner, more readable code.</p></li>
<li><p><strong>Early Termination</strong>: for and while loops allow for early termination, which can be more efficient when you're searching for a specific element.</p></li>
<li><p><strong>Large Arrays</strong>: For very large arrays, consider using for loops for better performance, especially if you need to break the loop early.</p></li>
<li><p><strong>Caching Array Length</strong>: In performance-critical situations, caching the array length in a variable before the loop can provide a slight speed improvement.</p></li>
<li><p><strong>Avoiding Array Resizing</strong>: When building an array dynamically, initializing it with a predetermined size (if possible) can improve performance by avoiding multiple array resizing operations.</p></li>
</ol>
<p></p><h2>
8. LeetCodeの練習問題
</h2>
<p>配列トラバーサル手法の理解をさらに深めるために、練習できる LeetCode の問題を 15 個紹介します。</p>
<ol>
<li>2つの合計</li>
<li>株式を売買するのに最適な時期</li>
<li>重複が含まれています</li>
<li>自己を除く配列の積</li>
<li>最大サブ配列</li>
<li>ゼロを移動</li>
<li>3合計</li>
<li>ほとんどの水が入った容器</li>
<li>配列を回転</li>
<li>回転ソートされた配列の最小値を見つける</li>
<li>回転ソート配列で検索</li>
<li>マージ間隔</li>
<li>スパイラルマトリックス</li>
<li>行列のゼロを設定</li>
<li>最長連続シーケンス</li>
</ol>
<p>これらの問題は、配列トラバーサル手法の広範囲をカバーしており、このブログ投稿で説明した概念を適用するのに役立ちます。</p>
<p></p>
<h2>
9. 結論
</h2>
<p>配列トラバーサルは、多くのアルゴリズムやデータ操作の基礎を形成するプログラミングの基本的なスキルです。基本的な for ループから、スライディング ウィンドウや特殊な行列トラバーサルなどの高度なテクニックまで、これらのメソッドをマスターすると、複雑な問題を効率的に解決する能力が大幅に向上します。</p>
<p>これら 20 の例を通しておわかりのように、JavaScript は配列トラバーサルのための豊富なツール セットを提供しており、それぞれに独自の長所と使用例があります。各テクニックをいつどのように適用するかを理解することで、プログラミングの幅広い課題に対処する準備が整います。</p>
<p>熟練するための鍵は練習であることを忘れないでください。これらの走査メソッドを自分のプロジェクトに実装してみて、基本に慣れてきたら、躊躇せずにさらに高度なテクニックを試してみてください。提供される LeetCode の問題は、これらの概念をさまざまなシナリオに適用する十分な機会を提供します。</p>
<p>スキルを磨き続けるときは、選択した走査方法がパフォーマンスに与える影響を常に念頭に置いてください。単純な for ループが最も効率的なソリューションである場合もありますが、スライディング ウィンドウや 2 ポインター メソッドなどのより特殊なテクニックが最適な場合もあります。</p>
<p>コーディングを楽しんでください。配列が常に効率的に走査されますように!</p>
以上がJavaScript を使用した DSA の配列トラバーサル: 基本から高度なテクニックまでの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 JavaScriptの文字列文字を交換しますMar 11, 2025 am 12:07 AM
JavaScriptの文字列文字を交換しますMar 11, 2025 am 12:07 AMJavaScript文字列置換法とFAQの詳細な説明 この記事では、javaScriptの文字列文字を置き換える2つの方法について説明します:内部JavaScriptコードとWebページの内部HTML。 JavaScriptコード内の文字列を交換します 最も直接的な方法は、置換()メソッドを使用することです。 str = str.replace( "find"、 "置換"); この方法は、最初の一致のみを置き換えます。すべての一致を置き換えるには、正規表現を使用して、グローバルフラグGを追加します。 str = str.replace(/fi
 独自のAjax Webアプリケーションを構築しますMar 09, 2025 am 12:11 AM
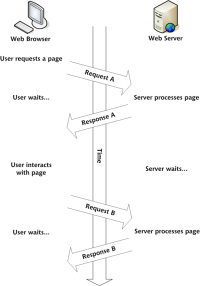
独自のAjax Webアプリケーションを構築しますMar 09, 2025 am 12:11 AMそれで、あなたはここで、Ajaxと呼ばれるこのことについてすべてを学ぶ準備ができています。しかし、それは正確には何ですか? Ajaxという用語は、動的でインタラクティブなWebコンテンツを作成するために使用されるテクノロジーのゆるいグループ化を指します。 Ajaxという用語は、もともとJesse Jによって造られました
 独自のJavaScriptライブラリを作成および公開するにはどうすればよいですか?Mar 18, 2025 pm 03:12 PM
独自のJavaScriptライブラリを作成および公開するにはどうすればよいですか?Mar 18, 2025 pm 03:12 PM記事では、JavaScriptライブラリの作成、公開、および維持について説明し、計画、開発、テスト、ドキュメント、およびプロモーション戦略に焦点を当てています。
 ブラウザでのパフォーマンスのためにJavaScriptコードを最適化するにはどうすればよいですか?Mar 18, 2025 pm 03:14 PM
ブラウザでのパフォーマンスのためにJavaScriptコードを最適化するにはどうすればよいですか?Mar 18, 2025 pm 03:14 PMこの記事では、ブラウザでJavaScriptのパフォーマンスを最適化するための戦略について説明し、実行時間の短縮、ページの負荷速度への影響を最小限に抑えることに焦点を当てています。
 jQueryマトリックス効果Mar 10, 2025 am 12:52 AM
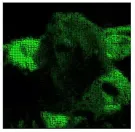
jQueryマトリックス効果Mar 10, 2025 am 12:52 AMマトリックスの映画効果をあなたのページにもたらしましょう!これは、有名な映画「The Matrix」に基づいたクールなJQueryプラグインです。プラグインは、映画の古典的な緑色のキャラクター効果をシミュレートし、画像を選択するだけで、プラグインはそれを数値文字で満たされたマトリックススタイルの画像に変換します。来て、それを試してみてください、それはとても面白いです! それがどのように機能するか プラグインは画像をキャンバスにロードし、ピクセルと色の値を読み取ります。 data = ctx.getimagedata(x、y、settings.greasize、settings.greasize).data プラグインは、写真の長方形の領域を巧みに読み取り、jQueryを使用して各領域の平均色を計算します。次に、使用します
 ブラウザ開発者ツールを使用してJavaScriptコードを効果的にデバッグするにはどうすればよいですか?Mar 18, 2025 pm 03:16 PM
ブラウザ開発者ツールを使用してJavaScriptコードを効果的にデバッグするにはどうすればよいですか?Mar 18, 2025 pm 03:16 PMこの記事では、ブラウザ開発者ツールを使用した効果的なJavaScriptデバッグについて説明し、ブレークポイントの設定、コンソールの使用、パフォーマンスの分析に焦点を当てています。
 シンプルなjQueryスライダーを構築する方法Mar 11, 2025 am 12:19 AM
シンプルなjQueryスライダーを構築する方法Mar 11, 2025 am 12:19 AMこの記事では、jQueryライブラリを使用してシンプルな画像カルーセルを作成するように導きます。 jQuery上に構築されたBXSLiderライブラリを使用し、カルーセルをセットアップするために多くの構成オプションを提供します。 今日、絵のカルーセルはウェブサイトで必須の機能になっています - 1つの写真は千の言葉よりも優れています! 画像カルーセルを使用することを決定した後、次の質問はそれを作成する方法です。まず、高品質の高解像度の写真を収集する必要があります。 次に、HTMLとJavaScriptコードを使用して画像カルーセルを作成する必要があります。ウェブ上には、さまざまな方法でカルーセルを作成するのに役立つ多くのライブラリがあります。オープンソースBXSLiderライブラリを使用します。 BXSLiderライブラリはレスポンシブデザインをサポートしているため、このライブラリで構築されたカルーセルは任意のものに適合させることができます
 Angularを使用してCSVファイルをアップロードおよびダウンロードする方法Mar 10, 2025 am 01:01 AM
Angularを使用してCSVファイルをアップロードおよびダウンロードする方法Mar 10, 2025 am 01:01 AMデータセットは、APIモデルとさまざまなビジネスプロセスの構築に非常に不可欠です。これが、CSVのインポートとエクスポートが頻繁に必要な機能である理由です。このチュートリアルでは、Angular内でCSVファイルをダウンロードおよびインポートする方法を学びます


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 中国語版
中国語版、とても使いやすい

PhpStorm Mac バージョン
最新(2018.2.1)のプロフェッショナル向けPHP統合開発ツール

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

ホットトピック
 7441
7441 15
15 1371
1371 52
52


